Линейные уравнения 7 класс: сложные примеры для тренировки и развернутые ответы

Линейные уравнения – одна из основных тем, которую изучают в седьмом классе математики. Как правило, первые задачи не представляют большой сложности и позволяют ученикам освоить основные принципы решения таких уравнений. Однако, в ходе обучения встречаются и более сложные примеры, требующие дополнительной тренировки. Решение таких уравнений требует не только уверенных знаний правил и формул, но и тщательного анализа условий задачи. Сложные примеры помогают ученикам развивать логическое мышление, умение находить различные пути решения и проверять свои ответы. Поэтому, для тренировки и закрепления навыков, предлагаются линейные уравнения 7 класс сложные примеры. Важно понимать, что с ростом сложности задач, ученикам потребуется больше времени и усилий для их решения.

Содержание

Найдем значения переменных
Уравнения с одной переменной
Уравнения с двумя переменными
Смешанные уравнения
Линейные уравнения 7 класс сложные примеры для тренировки
Пример 1:
Пример 2:
Пример 3:
Пример 4:
Пример 5:

Найдем значения переменных

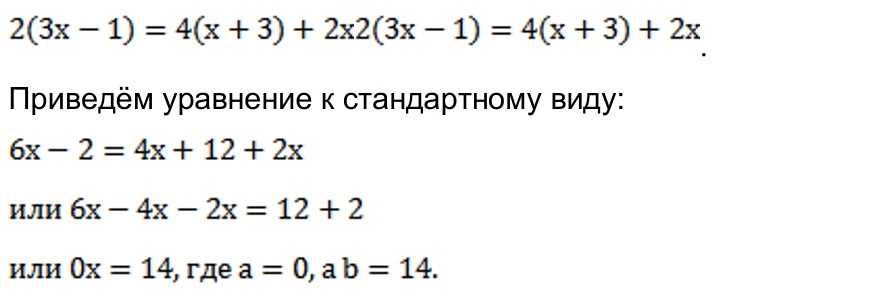
Часто нам приходится сталкиваться с уравнениями вида ax + b = c, где a, b и c – это некоторые числа или выражения, а x – переменная, значение которой мы хотим найти. Не стоит пугаться, если решение уравнения кажется сложным – я уверен, что мы справимся!

Для того чтобы найти значение переменной x, нужно применить принципы алгебры и выполнить несколько простых действий. Давайте рассмотрим несколько примеров, чтобы разобраться подробнее.

Пример 1:

Решим уравнение 3x + 5 = 14. Наша задача – найти значение переменной x.

Для начала, давайте избавимся от числа 5 на левой стороне уравнения. Для этого вычтем 5 из обеих частей:

3x + 5 — 5 = 14 — 5

3x = 9

Теперь у нас получилось уравнение 3x = 9. Для того чтобы найти значение переменной x, нужно разделить обе части уравнения на число 3:

3x / 3 = 9 / 3

x = 3

Ответ: значение переменной x равно 3.

Пример 2:

Теперь решим уравнение 2(4 — x) = 10. Задача – найти значение переменной x.

Давайте начнем с раскрытия скобок:

2 * 4 — 2 * x = 10

8 — 2x = 10

Теперь избавимся от числа 8 на левой стороне уравнения. Вычтем 8 из обеих частей:

8 — 8 — 2x = 10 — 8

-2x = 2

Для нахождения значения переменной x, разделим обе части уравнения на число -2. Не забудьте, что при делении на отрицательное число знак не меняется:

(-2x) / -2 = 2 / -2

x = -1

Ответ: значение переменной x равно -1.

Надеюсь, эти примеры помогут вам лучше понять процесс нахождения значений переменных в линейных уравнениях. Практикуйтесь, ставьте перед собой задачи и ищите решения. Вы удивитесь, насколько математика может быть интересной и вдохновляющей!

Желаю вам успехов и отличных результатов! Не бойтесь экспериментировать и находить новые пути к решению задач.

Уравнения с одной переменной

Возможно, ты уже слышал о понятии «уравнение». Оно представляет собой математическое выражение, в котором есть неизвестная переменная, которую надо найти. А в линейном уравнении переменная входит только в первой степени и не имеет отрицательных степеней или иррациональных значений.

Также, у нас есть правило — можем прибавить одну и ту же величину к обеим частям уравнения, и оно останется верным. Например, решим такое уравнение: 2x = 10. Сначала мы должны избавиться от 2, только так мы сможем найти значение x. И чтобы это сделать, мы можем разделить обе части уравнения на 2. Таким образом, получим x = 5.

Интересно, как линейные уравнения можно использовать в повседневной жизни? Представь, что нужно решить задачку находить расстояние, скорость или время. Линейные уравнения станут отличным помощником в решении таких задач. Они помогут тебе выразить одну величину через другую и найти неизвестное значение.

Например, предположим, что ты едешь на машине со скоростью 60 км/час и хочешь узнать, за сколько времени ты преодолеешь расстояние в 180 километров. Нам известны две величины — скорость и расстояние, и мы хотим найти время. Воспользуемся формулой скорости, которая выглядит следующим образом: V = S/t, где V — скорость, S — расстояние и t — время. Если мы перепишем эту формулу в виде линейного уравнения, то получим t = S/V. Подставим известные величины и получим t = 180/60 = 3 часа.

Вот и все! Теперь ты знаешь, что такое линейные уравнения с одной переменной и как их использовать в повседневной жизни. Практикуйся и не бойся задавать вопросы, математика — это удивительный мир, который открывает новые возможности и помогает лучше понимать мир вокруг нас!

Уравнения с двумя переменными

Зачем нам нужны уравнения с двумя переменными? Во-первых, они позволяют нам описывать зависимости между двумя величинами. Во-вторых, они помогают решать различные задачи, связанные с геометрией, физикой, экономикой и другими науками.

Линейные уравнения с двумя переменными имеют следующий вид: ax + by = c, где a, b и c — это коэффициенты, которые принадлежат множеству действительных чисел.

Давайте рассмотрим пример. У нас есть уравнение: 2x + 3y = 12. Здесь a = 2, b = 3 и c = 12. Наша задача состоит в том, чтобы найти такие значения x и y, которые удовлетворяют этому уравнению.

Если мы знаем одно из значений x или y, мы можем легко найти другое значение, используя данное уравнение. Например, если мы знаем значение x, то мы можем найти значение y, подставив его в уравнение и решив полученное уравнение относительно y.

Что делать, если у нас нет информации о значениях переменных? В этом случае нам требуется еще одно уравнение, чтобы найти значения x и y. Когда у нас есть два уравнения с двумя переменными, мы можем решить их вместе, используя методы подстановки, сложения или вычитания.

Иногда уравнения с двумя переменными могут иметь бесконечно много решений. Это значит, что существует бесконечно много пар значений x и y, которые удовлетворяют уравнению. Такие уравнения называются совместными. Они могут быть полными или неполными.

Что если уравнения неразрешимы? В этом случае они не имеют общих решений и называются несовместными. Это означает, что нет таких значений x и y, которые бы удовлетворяли обоим уравнениям одновременно.

Надеюсь, что этот небольшой экскурс помог тебе понять, что такое уравнения с двумя переменными и как их решать. Помни, практика делает мастера, поэтому тренируйся на различных примерах, чтобы стать настоящим экспертом в этой области. Удачи!

Смешанные уравнения

Чтобы упростить процесс решения смешанного уравнения, можно следовать нескольким шагам:

Найти все участки уравнения, включающие переменные и неизвестные коэффициенты.
Определить, какие единицы измерений соответствуют каждому из этих участков.
Привести все единицы измерений к одной системе мер, если это необходимо.
Разделить уравнение на соответствующие коэффициенты.
Вычислить значение неизвестной величины.

Давайте рассмотрим пример смешанного уравнения:

Пример:

Найти значение переменной x в уравнении: 6x — 4 = 10.

В данном уравнении переменной является x, а коэффициенты соответствуют единицам измерения. Сначала вычтем 4 из обеих сторон уравнения:

6x — 4 — 4 = 10 — 4

Теперь уравнение примет вид:

6x = 6

Далее разделим обе стороны уравнения на 6:

6x/6 = 6/6

x = 1

Таким образом, значение переменной x равно 1.

Смешанные уравнения являются важным элементом алгебры и широко используются в реальной жизни для решения различных задач. На практике мы можем сталкиваться с уравнениями, содержащими переменные и коэффициенты с единицами измерения, которые нам нужно решить, чтобы получить конкретные значения.

И помни – практика делает мастера! Чем больше задач ты попытаешься решить, тем лучше ты станешь в решении смешанных уравнений. Не бойся экспериментировать и искать разные подходы к решению – и ты обязательно достигнешь успеха!

Линейные уравнения 7 класс сложные примеры для тренировки

Линейные уравнения представляют собой математические выражения, в которых неизвестное значение переменной присутствует только в первой степени. Здесь представлены сложные примеры линейных уравнений, которые помогут тренировать навыки решения таких уравнений.