
Аксиома и лемма – два понятия, которые широко используются в математике и логике. Несмотря на некоторую схожесть, они имеют отличия и различное применение.
Лемма же – это промежуточное утверждение, которое служит для доказательства более сложной теоремы. Леммы могут использоваться в процессе решения задач и создания более общих утверждений.
Как правило, аксиомы считаются всеобщими и необходимыми для основания теории, в то время как леммы являются вспомогательными и имеют более узкую область применения.
Понимание различия между аксиомами и леммами важно для развития математической логики и доказательств.
Определение аксиомы

Аксиомы являются ключевыми элементами в математике и различных научных дисциплинах. Они не только обозначают истинность определенных утверждений, но и определяют некоторые базовые свойства или отношения. Аксиомы обладают высокой степенью вероятности, их принимают безусловно и считают фундаментом для дальнейшего исследования.
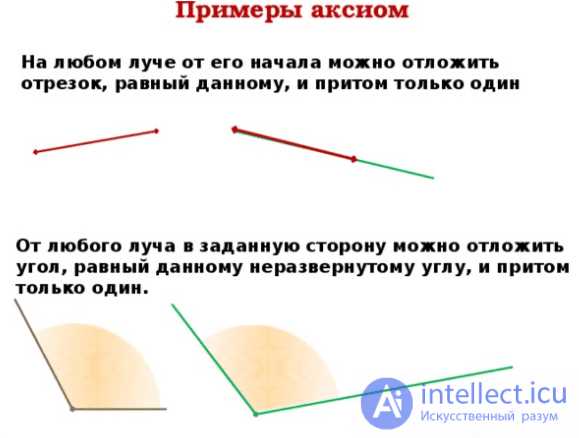
Примеры аксиом:
- Аксиома вещественных чисел: для любых чисел a и b существуют операции сложения и умножения такие, что сумма и произведение остаются числами.
- Аксиома о соотношении эквивалентности: если a, b и c являются эквивалентными элементами, то a = b и b = c влекут a = c.
- Аксиома о переменной: квадрат разности двух чисел равен разности квадратов этих чисел.
Аксиомы могут быть основанными на простых и интуитивных идеях, либо сложными и построенными на основе множества других аксиом. Важно понимать, что аксиомы представляют собой неопровержимую истину, которая существует независимо от наших рассуждений и мнений.
Итак, аксиома – это незыблемое утверждение, которое служит основой для построения математических теорий и научных дисциплин.
Определение леммы
В отличие от аксиомы, которая считается сразу истинной и не требует доказательства, лемма обычно нуждается в доказательстве, чтобы быть принятой как истинная. Лемма, позволяющая доказать какую-то теорему, может быть простой и очевидной, а может быть и сложной и требующей более глубокого анализа.
Одной из основных целей леммы является упрощение доказательств исходной теоремы. Путем разбиения доказательства на более мелкие части, лемма позволяет увидеть более ясную картину и облегчить понимание общего результата. Она создает логическую связь между исходной теоремой и более простыми, но не менее важными утверждениями.
Важно понимать, что лемма может быть использована не только для доказательства теоремы, но и для создания новых математических результатов. Она может быть основой для дальнейшего исследования и открытия новых связей и закономерностей. На самом деле, множество математических теорий и формулировок основываются на леммах, которые помогают установить взаимосвязи между различными понятиями и дать более полное представление о теме.
Таким образом, лемма является неотъемлемой частью математического исследования. Она помогает упростить и анализировать сложные проблемы, объединяет различные понятия и является отправной точкой для получения новых результатов. Без использования леммы многие математические теории и их приложения были бы невозможными.
Отличия между аксиомой и леммой
Итак, вы интересуетесь различием между аксиомой и леммой. Давайте рассмотрим оба этих понятия более подробно и выясним, как они взаимосвязаны.
Аксиома: основа всего
Примером аксиомы может служить аксиома о равенстве в геометрии, которая гласит, что любые две одинаковые величины равны друг другу. Эта аксиома принимается безусловно, и на ее основе строятся все остальные утверждения и доказательства.
Лемма: вспомогательное утверждение
Лемма, с другой стороны, является вспомогательным утверждением или вспомогательной теоремой, которая используется для доказательства более общих теорем. В отличие от аксиомы, лемма требует доказательства перед тем, как ее можно использовать для доказательства других утверждений.
Леммы служат промежуточными шагами в процессе доказательства более сложных теорем. Они помогают сужать область поиска и предоставляют дополнительные основы для доказательства. Часто леммы формулируются и доказываются отдельно, до того как они используются в основном доказательстве.
Применение аксиом и лемм
Аксиомы и леммы широко применяются в науке, математике и философии. Они представляют собой инструменты для построения логических систем и доказательств.
Кроме того, аксиомы и леммы могут быть использованы для доказательства теорем и утверждений. Их доказательство требует строгих логических рассуждений и следования точным правилам.
Аксиома и лемма: отличия и применение

Аксиома
Аксиома — это основное утверждение или предположение, которое принимается без доказательства. Она считается истинной на основе собственного определения или соглашения. Аксиомы используются для построения математической системы или теории.
Аксиома не нуждается в обосновании и принимается как основа для дальнейших рассуждений. В математике существуют различные аксиоматические системы, например, «аксиомы Пеано» для арифметики натуральных чисел или «аксиомы Евклида» для геометрии.
Лемма
Лемма — это вспомогательное утверждение, которое используется для доказательства более общей теоремы. Леммы не имеют самостоятельной ценности и используются только в контексте более крупных теорем или задач. Они помогают упростить или сузить область рассмотрения исследуемой проблемы
Леммы обычно являются специальными случаями теорем и имеют более ограниченное применение. Они могут быть использованы многократно для доказательства различных теорем. Леммы могут быть доказаны как автономные утверждения, но их главная цель — подтверждение или обоснование основной теоремы.
Применение аксиомы и леммы
Аксиомы играют важную роль в развитии математики, так как они служат основными истинами для построения математических систем. Они определяют основные понятия и правила, на основе которых строится всё математическое рассуждение. Аксиомы позволяют формализовать и описать математическую реальность и проявлять ее законы.
Леммы, с другой стороны, облегчают доказательство теорем и помогают строить более сложные рассуждения. Они предоставляют дополнительные знания или свойства, которые используются для решения задач и выведения более общих результатов.
В целом, аксиомы и леммы — это инструменты, которые позволяют формально и убедительно доказать математические утверждения и построить математическую теорию. Они являются основой для развития математики и науки в целом.


