Алгоритмы являются основой математики и играют важную роль в решении различных задач. Они представляют собой последовательность шагов, которые позволяют решить определенную проблему. Базовыми понятиями алгоритмов являются входные данные, выходные данные и операции, которые необходимо выполнить для получения результата. В математике алгоритмы применяются для решения уравнений, поиска минимума или максимума, построения графиков и многих других задач. Они позволяют автоматизировать решение сложных математических задач и сэкономить время и усилия. Изучение алгоритмов имеет большое значение для развития математического мышления и позволяет углубить понимание основных принципов и методов решения математических задач.
- Определение алгоритма
- Определение
- Основные свойства алгоритма
- 1. Дискретность
- 2. Детерминированность
- 3. Конечность
- 4. Возможность выполнения
- 5. Эффективность
- Применение алгоритмов в математике
- Примеры применения алгоритмов в математике:
- Арифметические алгоритмы
- Геометрические алгоритмы
- Алгоритмы в математике: базовые понятия и применение
- Примеры применения алгоритмов в математике:
Определение алгоритма
Алгоритмы часто используются в математике для решения сложных задач. Они могут быть использованы, например, для вычисления чисел Фибоначчи или нахождения корня квадратного числа. Алгоритмы также широко применяются в программировании, где они служат основой для написания программ и приложений.
Основная идея алгоритма состоит в том, чтобы разбить сложную задачу на более простые подзадачи, которые можно решить последовательно. Каждый шаг в алгоритме должен быть ясным и однозначным, так чтобы его можно было выполнить без неоднозначности или произвольности. Используя алгоритм, можно достичь того, чтобы сложная задача стала более управляемой и решаемой.
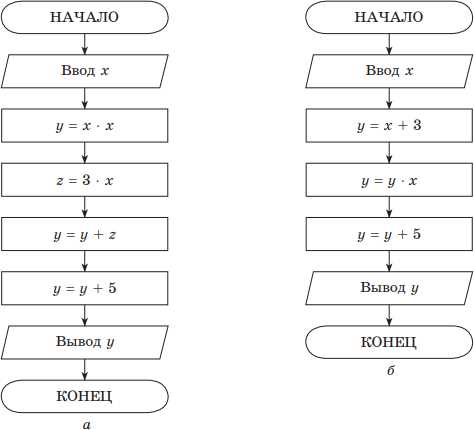
Алгоритмы могут быть представлены в различных формах и способах записи. Они могут быть описаны словесно, с использованием псевдокода или конкретного языка программирования. Важно, чтобы алгоритм был понятным и легко читаемым, чтобы люди могли его использовать и понимать. Однако алгоритмы также могут быть представлены в виде блок-схемы или диаграммы, чтобы визуально представить последовательность шагов.
Алгоритмы играют важную роль в нашей жизни, даже если мы не всегда осознаем это. Например, когда мы следуем рецепту при приготовлении пищи или следуем инструкциям по сборке мебели, мы фактически используем алгоритмы для достижения желаемого результата. Они помогают нам систематизировать задачи и сделать их более эффективными.
Определение
Алгоритмы могут быть представлены в различных формах, например, в виде текстового описания, блок-схемы, диаграммы или программного кода. Они могут быть простыми и линейными, либо сложными и ветвящимися.
Основная идея алгоритма заключается в том, что он позволяет человеку или компьютеру последовательно выполнять определенные действия, чтобы достичь желаемого результата. Он определяет порядок действий, условия и циклы, которые должны быть выполнены для достижения цели.
Алгоритмы в математике являются неотъемлемой частью решения различных задач. Они могут быть использованы для решения уравнений, нахождения корней, выполнения математических операций, оценки функций и многого другого. Алгоритмический подход позволяет сделать математические вычисления более систематичными и эффективными.
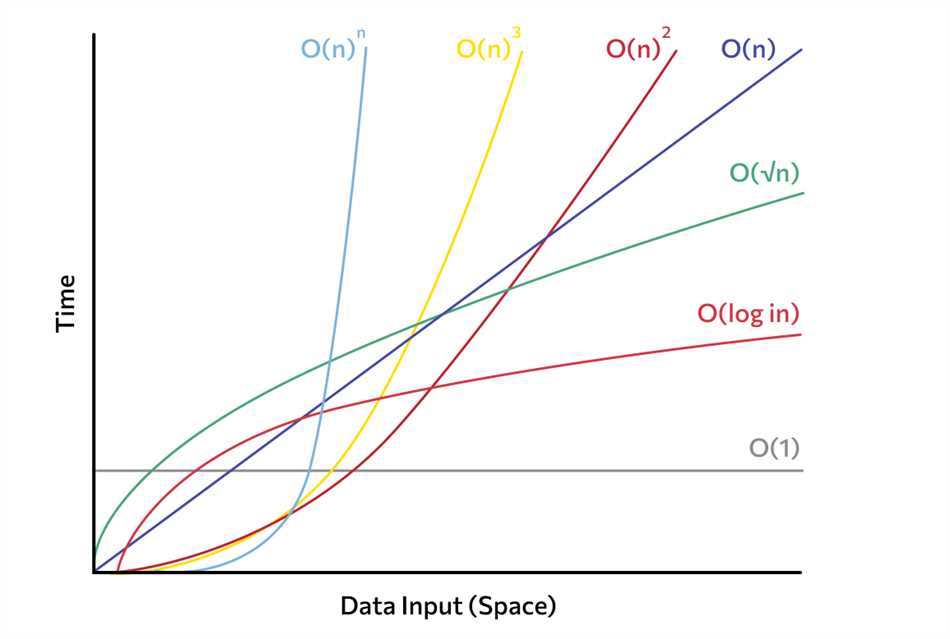
Одним из важных аспектов алгоритма является его эффективность. Это означает, что алгоритм должен быть оптимальным и занимать минимальное время и ресурсы для его выполнения. Это особенно важно для больших задач или вычислений с ограниченными ресурсами.
Важно понимать, что алгоритмы могут быть различными и должны быть выбраны в зависимости от конкретной задачи. Однако, независимо от выбранного алгоритма, он должен быть логичным, последовательным и понятным для его исполнителя.
В конечном итоге, алгоритмы позволяют нам разбить сложные задачи на более простые и понятные компоненты, что облегчает их решение. Они являются фундаментальным инструментом для достижения успеха в математике и других научных и технических областях.
Основные свойства алгоритма
1. Дискретность
Алгоритм должен состоять из отдельных, раздельных шагов. Это означает, что каждый шаг должен быть четко определен и отделен от других шагов. Дискретность алгоритма позволяет ему быть выполненным пошагово, легко проверяемым и изменяемым при необходимости.
2. Детерминированность
Алгоритм должен быть детерминированным, это значит, что он должен давать одинаковый результат при одинаковых входных данных. С другими словами, каждый шаг алгоритма должен быть определен однозначно и предсказуемо, не зависимо от внешних условий или случайных факторов.
3. Конечность
Алгоритм должен иметь конечное число шагов, в противном случае он никогда не завершит свою работу. Конечность гарантирует, что алгоритм можно выполнить за определенное время и получить результат.
4. Возможность выполнения
Алгоритм должен быть выполнимым, то есть каждый шаг должен быть реализован таким образом, чтобы его можно было реализовать на некотором устройстве или исполнить каким-либо способом. Важно учесть, что алгоритм должен быть выполним на практике, а не только в теории.
5. Эффективность
Алгоритм должен быть эффективным, то есть выполнять задачу с минимальными затратами времени и ресурсов. Эффективность может быть определена различными способами, например, скоростью выполнения или использованием минимального количества памяти.
Важно понимать, что эти свойства не являются абсолютными стандартами, и алгоритмы могут различаться в своих характеристиках. Некоторые алгоритмы могут быть более эффективными, чем другие, но все они должны соответствовать указанным основным свойствам. Эти свойства позволяют нам оценить качество и надежность алгоритма и выбрать оптимальное решение для решения конкретной задачи.
Применение алгоритмов в математике
Алгоритмы имеют широкое применение в математике, помогая решать различные задачи и облегчая изучение и понимание математических концепций. Они представляют собой последовательность шагов или правил, которые приводят к определенному результату.
Одним из основных применений алгоритмов в математике является решение уравнений. Например, для решения линейного уравнения можно использовать алгоритм подстановки или алгоритм Гаусса. Эти алгоритмы позволяют найти значения переменных, удовлетворяющие данному уравнению.
Алгоритмы также используются в математическом анализе для вычисления пределов функций, производных и интегралов. Например, для вычисления значения предела функции на бесконечности можно применить алгоритм Лопиталя или методы численного интегрирования для вычисления приближенного значения определенного интеграла.
Еще одним важным применением алгоритмов в математике является решение задач оптимизации. Алгоритмы оптимизации помогают найти наилучшие значения переменных, удовлетворяющие определенным ограничениям. Например, алгоритмы линейного программирования применяются для решения задачи максимизации или минимизации линейной функции при линейных ограничениях.
Примеры применения алгоритмов в математике:
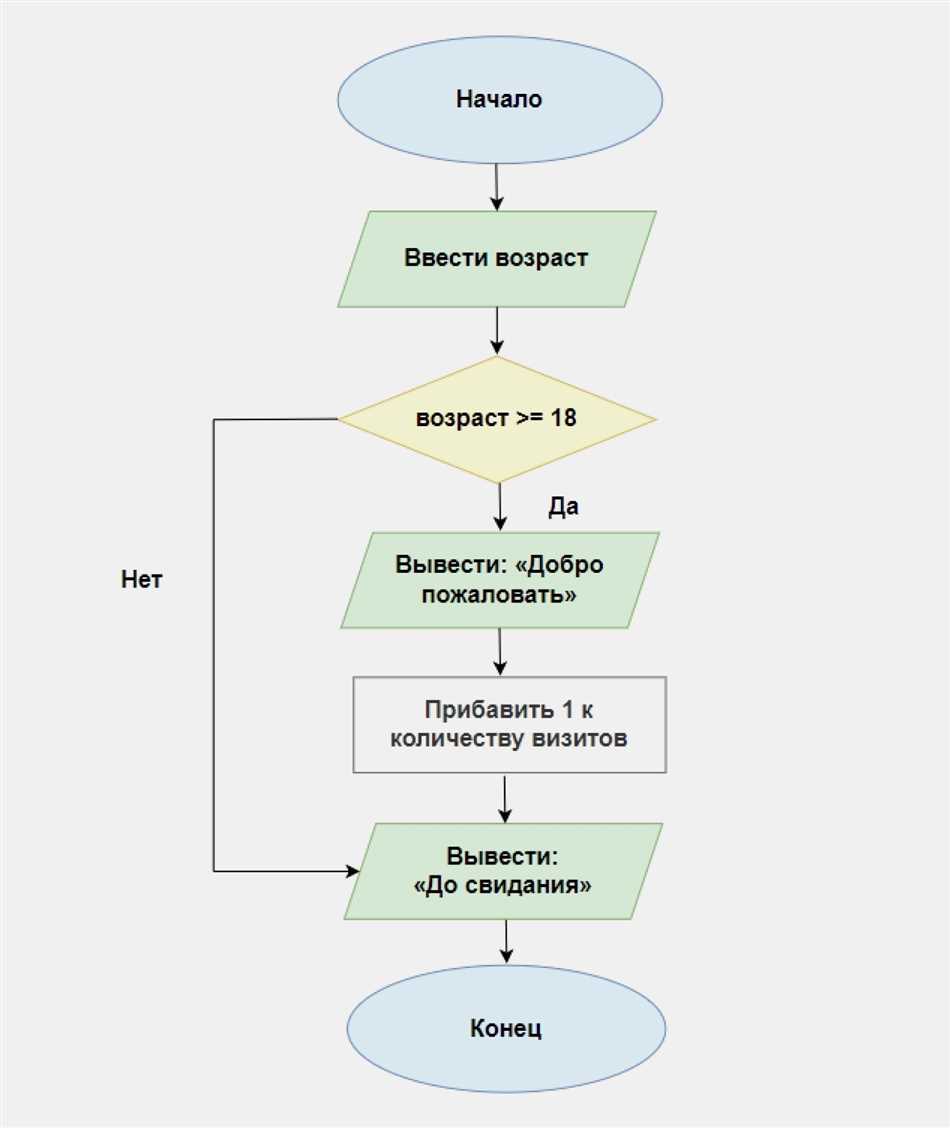
- Решение уравнений и систем уравнений.
- Вычисление пределов функций.
- Вычисление производных и интегралов.
- Решение задач оптимизации.
- Поиск корней функций.
- Работа с матрицами и векторами.
Также алгоритмы используются в геометрии, комбинаторике, теории чисел и других областях математики. Они помогают систематизировать и упростить решение задач, экономя время и усилия.
Применение алгоритмов в математике имеет огромное значение и является неотъемлемой частью изучения и практического применения математических концепций. Они помогают решать широкий спектр задач, упрощают расчеты и дают возможность получить точные и надежные результаты. Важно овладеть базовыми алгоритмическими навыками и уметь выбирать подходящий алгоритм для каждой конкретной задачи, чтобы достичь наилучших результатов.
Арифметические алгоритмы
Зачем нам нужны эти алгоритмы, если у нас есть калькуляторы и компьютеры, которые могут выполнить эти операции за нас? Дело в том, что понимание алгоритмов позволяет нам не только лучше понять, как работает математика, но и развить свои когнитивные навыки, логическое мышление, умение решать проблемы и анализировать данные.
Ключевым преимуществом арифметических алгоритмов является их универсальность — они могут быть применены во многих различных ситуациях. Независимо от того, занимаетесь ли вы бухгалтерией, физикой, программированием или просто решаете повседневные задачи, знание и понимание арифметических алгоритмов поможет вам во всех аспектах жизни.
Давайте рассмотрим некоторые из основных арифметических алгоритмов:
- Сложение: это базовая операция, которая позволяет нам суммировать два или более числа. Например, чтобы сложить числа 5 и 7, мы начинаем с первого числа (5) и прибавляем к нему второе число (7), получая в итоге сумму 12.
- Вычитание: это операция, обратная сложению. Она позволяет нам вычесть одно число из другого. Например, чтобы вычесть число 3 из числа 8, мы начинаем с первого числа (8) и вычитаем из него второе число (3), получая в итоге разность 5.
- Умножение: это операция, которая позволяет нам увеличить число путем повторного сложения. Например, чтобы умножить число 4 на 3, мы начинаем с первого числа (4) и прибавляем его к себе два раза, получая в итоге произведение 12.
- Деление: это операция, которая позволяет нам разделить одно число на другое. Например, чтобы разделить число 10 на число 2, мы делим первое число (10) на второе (2), получая в итоге частное 5.
Арифметические алгоритмы являются базовыми строительными блоками для более сложных математических операций и алгоритмов. Например, для решения уравнений, работы с дробями, вычисления корней и многое другое, мы используем комбинацию различных арифметических алгоритмов.
Теперь, когда вы знаете, что такое арифметические алгоритмы и как они применяются в математике и повседневной жизни, вы можете начать исследовать их дальше. Попробуйте самостоятельно решать задачи и применять арифметические алгоритмы в практике. Это поможет вам развивать свои навыки и найти новые интересные способы применения математики в своей жизни.
Геометрические алгоритмы
Применение геометрических алгоритмов обширно в различных областях, таких как компьютерная графика, компьютерное зрение, игровая разработка, робототехника и многие другие. Эти алгоритмы играют ключевую роль в создании визуальных эффектов, анимации, поиска путей, оптимизации задач и решении сложных математических проблем.
Одним из базовых геометрических алгоритмов является алгоритм Брезенхема для построения линии на плоскости. С его помощью можно создавать плавные и четкие линии на экране, что особенно полезно в компьютерной графике и растровой графике. Этот алгоритм основывается на работе с дискретными большинством технологий управления дискретным поведением объектов. Этот алгоритм очень быстр и эффективен в реализации.
Другим примером геометрического алгоритма является алгоритм вычисления площади многоугольника. Этот алгоритм позволяет вычислить площадь многоугольника, заданного набором его вершин. Он основан на разбиении многоугольника на треугольники и последующем вычислении их площадей. Этот алгоритм находит широкое применение в геометрическом моделировании, анализе изображений и решении задач распознавания образов.
Геометрические алгоритмы также используются для решения задач нахождения пересечений объектов, построения выпуклой оболочки, определения видимости точек и многих других геометрических операций. Они представляют собой мощный инструмент для анализа и манипулирования геометрическими данными и позволяют решать сложные задачи эффективно и точно.
Ниже представлены примеры геометрических алгоритмов в виде списка:
- Алгоритм Брезенхема для построения линии на плоскости
- Алгоритм вычисления площади многоугольника
- Алгоритм нахождения пересечения двух отрезков
- Алгоритм построения выпуклой оболочки
- Алгоритм определения видимости точек в трехмерном пространстве
| Применение | Пример |
|---|---|
| Компьютерная графика | Алгоритм Брезенхема для построения линии на плоскости |
| Геометрическое моделирование | Алгоритм вычисления площади многоугольника |
| Компьютерное зрение | Алгоритм нахождения пересечения двух отрезков |
| Робототехника | Алгоритм построения выпуклой оболочки |
| Математическое моделирование | Алгоритм определения видимости точек в трехмерном пространстве |
Геометрические алгоритмы предоставляют мощный инструмент для работы с геометрическими данными и решения сложных задач. Их применение охватывает множество областей и способствует развитию новых технологий и инноваций. Изучение и понимание геометрических алгоритмов открывает перед нами мир возможностей в области математики и компьютерных наук.
Алгоритмы в математике: базовые понятия и применение
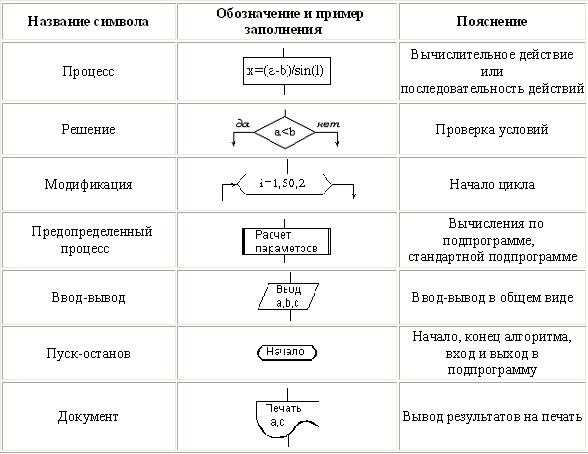
Алгоритмы могут быть использованы для решения простых и сложных задач. Они могут быть записаны на естественном языке или на языке программирования, а также представлены в виде блок-схемы или псевдокода. Одно из ключевых свойств алгоритма — его эффективность, то есть время выполнения и объем используемой памяти.
Примеры применения алгоритмов в математике:
- Алгоритм Евклида — используется для нахождения наибольшего общего делителя двух чисел. Он основан на повторении операции деления с остатком.
- Быстрое возведение в степень — это алгоритм, который позволяет эффективно возводить число в заданную степень, используя лишь несколько операций умножения.
- Алгоритм сортировки — существует множество алгоритмов сортировки, позволяющих упорядочить набор элементов по определенному критерию. Некоторые из них включают быструю сортировку, сортировку пузырьком и сортировку слиянием.
- Интегрирование функций — алгоритмы численного интегрирования позволяют вычислять значение определенного интеграла функции на заданном интервале. Одним из таких методов является метод трапеций.
- Поиск корней уравнений — алгоритмы поиска корней позволяют находить значения, при которых уравнение принимает нулевое значение. Некоторые из таких методов включают метод половинного деления и метод Ньютона.
- Алгоритмы оптимизации — используются для нахождения наилучшего решения оптимизационной задачи при заданных ограничениях. Примером такого алгоритма является метод градиентного спуска.