Когда мы говорим о числе элементов в натуральном ряду, мы обычно имеем в виду количество чисел в этом ряду. Натуральный ряд – это последовательность чисел, начинающаяся с единицы и продолжающаяся бесконечно. Понимание числа элементов в натуральном ряду помогает нам лучше понять и анализировать различные математические концепции и задачи.
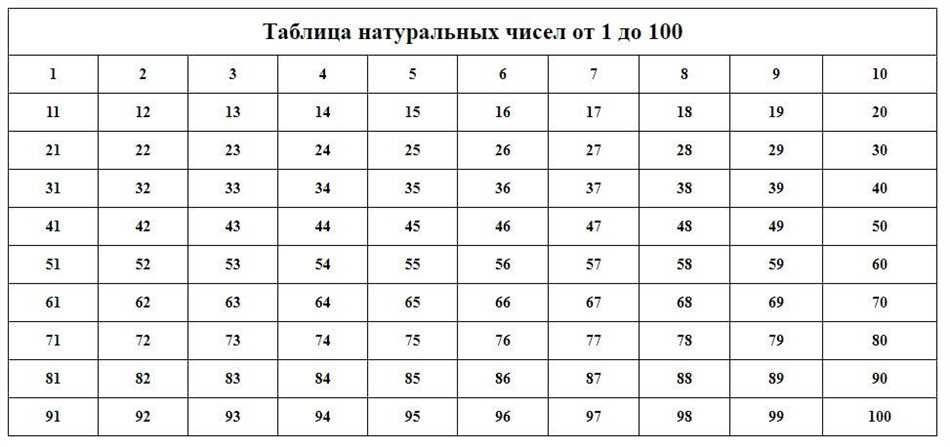
Давайте рассмотрим пример. Если мы говорим о числе элементов в ряду натуральных чисел до 10 включительно, то мы имеем в виду, что в данном ряду содержится 10 чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Здесь количество чисел соответствует числу элементов в ряду.
Также стоит отметить, что число элементов в натуральном ряду можно бесконечно увеличивать, добавляя к ряду все новые натуральные числа. Это позволяет нам изучать бесконечные последовательности и определять их свойства и закономерности.
Основные понятия
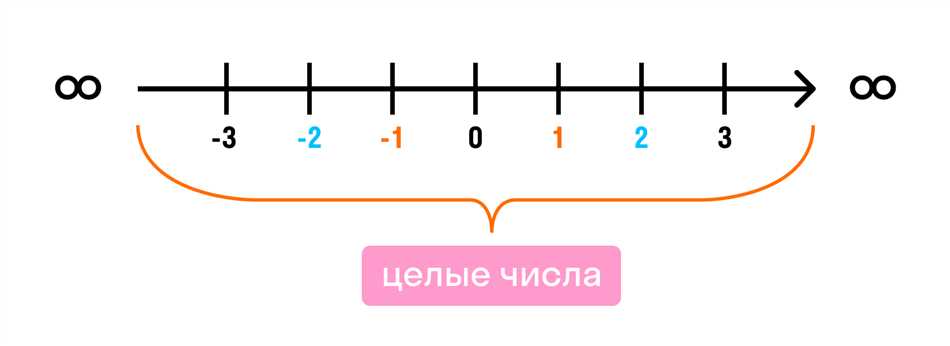
- Натуральные числа: Это все положительные числа, начиная с единицы и без дробной части. Натуральный ряд — это натуральные числа, упорядоченные по возрастанию.
- Элементы ряда: Они представляют собой числа, составляющие натуральный ряд. Например, элементами ряда от 1 до 10 являются числа 1, 2, 3 и так далее до 10.
- Первый и последний элементы: Первый элемент ряда — это наименьшее число в ряду, а последний элемент — наибольшее число.
- Число элементов: Оно определяет количество элементов в ряду. Например, число элементов в ряду от 1 до 10 равно 10.
- Последовательность: Это упорядоченный набор элементов. Натуральный ряд является примером последовательности.
Вот и все основные понятия, о которых тебе стоило узнать! Натуральные числа, элементы ряда, первый и последний элементы, число элементов и последовательность – все они важны для понимания темы числа элементов в натуральном ряду. Используй эти понятия, чтобы успешно решать задачи и развивать свои математические навыки. Удачи тебе!
Что такое натуральный ряд?
Возьмем, к примеру, натуральные числа от 1 до 10:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Это пример натурального ряда, где каждое число следует за предыдущим без пропусков.
Натуральный ряд имеет множество важных свойств и приложений. Он используется в математике для изучения счета, арифметики, геометрии и других областей. В реальной жизни мы также сталкиваемся с натуральными рядами: нумерация страниц в книге, учет товаров на складе или дни в году — все это примеры натуральных рядов.
Итак, натуральный ряд — это основа для понимания порядка и последовательности. Он помогает нам структурировать мир вокруг нас и является ключевым понятием в математике и нашей повседневной жизни.
Что такое число элементов в натуральном ряду?
Число элементов в натуральном ряду представляет собой количество упорядоченных чисел, расположенных в порядке возрастания или убывания. Однако это не просто количество, а скорее способ определить размер или общее число элементов в данном ряду.
Допустим, у нас есть натуральный ряд чисел, начинающийся с 1 и возрастающий на 1 с каждым следующим числом. Если мы хотим узнать, сколько чисел есть в этом ряду, мы можем использовать формулу для нахождения суммы арифметической прогрессии, учитывая начало и шаг прогрессии. Например, если хотим найти количество чисел в ряду до 10, формула будет выглядеть так:
n = (a1 + an) / d + 1
Где a1 — первое число в ряду, an — последнее число в ряду, d — шаг прогрессии, n — количество чисел в ряду.
Таким образом, количество элементов в натуральном ряду может быть установлено, используя формулу, которая зависит от начального числа и шага прогрессии. Это позволяет нам легко определить, сколько чисел будет в последовательности и использовать это знание в различных математических и практических задачах.
Примеры
Выбрать примеры для иллюстрации понятий и теорий всегда интересно. Давай попробуем представить несколько примеров, чтобы лучше понять, что такое число элементов в натуральном ряду.
Представь, что ты обедаешь и каждый день кладешь на тарелку на один горошину больше: первый день — одна горошина, второй — две, третий — три и так далее. Сколько горошин у тебя будет на десятом дне? Ну, конечно, 10! Это пример натурального ряда, где каждый элемент больше предыдущего на 1.
А что, если мы хотим посчитать количество ребер на треугольнике? На самом первом у нас будет 3 ребра. Затем мы добавляем еще одно ребро при каждом новом треугольнике. Так, на пятом треугольнике будет всего 15 ребер. Здесь мы также имеем дело с натуральным рядом, где каждый элемент больше предыдущего на 1.
Наши примеры помогают иллюстрировать, как рабоtatет число элементов в натуральном ряду. Интересно, какие примеры ты можешь придумать сам?
Примеры натуральных рядов
Что такое натуральный ряд? Это последовательность чисел, начинающаяся с единицы и продолжающаяся бесконечно. Натуральные ряды широко распространены и встречаются повсюду в нашей повседневной жизни.
Давайте рассмотрим несколько примеров натуральных рядов:
- Ряд натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и так далее. Этот ряд является простейшим примером натурального ряда, который мы встречаем ежедневно. Он бесконечно увеличивается, добавляя к каждому числу единицу.
- Ряд четных чисел: 2, 4, 6, 8, 10 и т.д. В этом ряду каждое последующее число больше предыдущего на 2. Он состоит только из четных чисел и также бесконечен.
- Ряд нечетных чисел: 1, 3, 5, 7, 9 и т.д. В этом ряду каждое последующее число больше предыдущего на 2. Этот ряд состоит только из нечетных чисел и продолжается до бесконечности.
Безусловно, эти примеры лишь капля в море. Возможно, вы сможете найти свои собственные натуральные ряды, которые отражают какие-то интересные закономерности или шаблоны.
Важно понимать, что натуральные ряды полны потенциала и могут быть использованы в различных сферах. Например, они могут помочь в решении задач математики, программирования и физики. Ряды могут также применяться для конструирования графиков, таблиц и прогнозов будущих событий.
Итак, натуральные ряды — это не только абстрактные концепции, но и мощный инструмент, который мы можем использовать в повседневной жизни. Раскройте свой творческий потенциал и создайте свои собственные удивительные натуральные ряды!
Как найти число элементов в натуральном ряду вручную?
Знаешь ли ты, что каждый натуральный ряд начинается с числа 1? Да, именно так! И мы можем использовать эту информацию, чтобы найти число элементов в таком ряду. Для этого важно знать последний элемент ряда.
Представь, что у нас есть натуральный ряд, который начинается с числа 1 и заканчивается числом, скажем, 10. Как мы можем найти число элементов в этом ряду?
Просто вычитаем первый элемент ряда из последнего и добавляем 1 (чтобы учесть первый элемент). В данном случае, это будет так: 10 — 1 + 1 = 10. Таким образом, число элементов в этом ряду равно 10.
Но что, если нам неизвестен последний элемент ряда? Не волнуйся, у нас есть другая формула, которую можно использовать. В этом случае, мы также знаем первый элемент ряда и разность между соседними элементами.
- 1 шаг: Найди разность между любыми двумя соседними элементами. Давай представим, что разность равна 2.
- 2 шаг: Вычти 1 из последнего элемента ряда.
- 3 шаг: Раздели результат из второго шага на разность между элементами.
- 4 шаг: Прибавь 1 к результату из третьего шага.
Вот и все! Теперь ты знаешь, как найти число элементов в натуральном ряду вручную, используя простые математические операции. Используй этот метод для нахождения числа элементов в ряду с любым первым и последним элементом, а также известной разностью между элементами.
Свойства чисел в натуральном ряду
Другое свойство натуральных чисел — их бесконечность. В отличие от конечных наборов чисел, натуральный ряд продолжается вечно, и нет ограничения сверху. Это позволяет использовать натуральные числа для описания бесконечных процессов и непрерывных изменений в различных областях знаний.
Кроме того, натуральные числа обладают свойством упорядоченности. Они расположены в порядке возрастания, и каждое число имеет свое уникальное значение. Это позволяет нам легко сравнивать и упорядочивать числа в ряду, а также использовать их для классификации и сортировки различных объектов и событий.
Еще одно важное свойство натуральных чисел — их способность образовывать арифметические и геометрические прогрессии. Арифметические прогрессии представляют собой последовательность чисел, в которой каждое следующее число получается путем прибавления постоянного числа (шага) к предыдущему. Геометрические прогрессии отличаются тем, что каждое следующее число получается путем умножения предыдущего числа на постоянное число (знаменатель). Эти два типа прогрессий широко используются в математике, физике, экономике и других науках.
Таким образом, свойства чисел в натуральном ряду делают их мощным инструментом для счета, описания и анализа различных явлений и процессов. Они помогают нам легко оперировать числами, упорядочивать их и создавать различные математические модели.
Сложение и вычитание чисел в натуральном ряду
Сможешь ли ты вспомнить, как складывать и вычитать числа в натуральном ряду? Давай вспомним!
Когда мы складываем два числа, мы объединяем их вместе, чтобы получить новое число. Например, если мы складываем 3 и 5, мы можем визуализировать это, представив себе 3 яблока и 5 яблок, которые мы сложили вместе. В результате получаем 8 яблок.
А теперь давай представим, что у нас есть начальное число 10, и мы хотим вычесть 4 от него. В этом случае мы будем удалять яблоки из нашей группы. У нас было 10 яблок, мы убрали 4 яблока и осталось 6 яблок.
Таким образом, когда мы складываем два числа, мы увеличиваем общее количество, а когда вычитаем, мы уменьшаем его. Просто представь себе, что у тебя есть группа предметов, и ты добавляешь или убираешь их. Вот и весь секрет.
Не забывай тренироваться в сложении и вычитании чисел, это очень полезное умение для повседневной жизни. Попробуй приложить его на практике, например, когда делаешь покупки в магазине или считаешь, сколько дней осталось до твоего дня рождения. Ты справишься!
Умножение и деление чисел в натуральном ряду

При умножении чисел в натуральном ряду получается произведение. Например, умножение числа 2 на число 3 дает результат 6 (2 * 3 = 6). Важно учитывать коммутативность данной операции: порядок умножаемых чисел не влияет на результат. Также существуют свойства ассоциативности и дистрибутивности при умножении чисел.
Деление в натуральном ряду позволяет найти частное двух чисел. Например, деление числа 8 на число 2 дает результат 4 (8 / 2 = 4). Важно обратить внимание на то, что не все числа можно поделить на определенное число без остатка. В этом случае мы получаем частное с остатком. Например, при делении числа 7 на число 3 получаем частное 2 и остаток 1 (7 / 3 = 2, остаток 1).
Умножение и деление чисел в натуральном ряду являются основными операциями, которые используются в различных областях науки и повседневной жизни. Понимание и применение данных операций позволяют нам решать разнообразные задачи и проводить вычисления с числами. Они также являются основой для изучения более сложных математических операций, таких как умножение и деление дробей, алгебры и т. д.