Область определения (ОО) – это все возможные значения, которые можно подставить вместо переменной в функцию так, чтобы получить корректный результат. ОО показывает, какие значения «допустимы» для данной функции. Например, если у нас есть функция f(x) = √x, то ОО будет состоять из всех неотрицательных чисел, так как корень из отрицательного числа не определен.
С другой стороны, область значений (ОЗ) – это все значения, которые функция может принимать в результате подстановки различных значений переменной. ОЗ определяет, какие значения могут быть «выходными» для функции. Например, функция f(x) = x^2 будет иметь ОЗ, состоящую из всех неотрицательных чисел, так как числа, возведенные в квадрат, всегда неотрицательны.
Итак, ОО – это множество «допустимых» входных значений, а ОЗ – множество «возможных» выходных значений. Знание ОО и ОЗ позволяет нам понять, какие значения переменной и результаты функции являются допустимыми в конкретной ситуации.
Определение функции
Для лучшего понимания, давай рассмотрим пример. Представь, что ты пекарь и твоя функция — это рецепт. Ты берешь определенные ингредиенты (входные значения), следуешь рецепту и в результате получаешь вкусный пирог (выходное значение). Вот и все! Функция — это инструкция, которая превращает входные данные в выходные.
Теперь давай обсудим область определения и область значений функции. Область определения — это набор всех входных значений, которые функция может принять. Снова вернемся к примеру с пирогом. Если у тебя есть список ингредиентов, которые ты используешь в своем рецепте, то это и есть область определения.
Область значений, с другой стороны, — это набор всех возможных выходных значений, которые функция может вернуть. В нашем случае, это было бы разнообразие вкусов пирогов, которые ты можешь приготовить.
Так что, разобрались? Функция — это инструкция, которая превращает входные данные в выходные, а область определения и область значений определяют границы того, что функция может принять и вернуть. Теперь ты можешь использовать этот знак в любых математических или программных задачах в дальнейшем. Удачи!
Что такое функция?
Функция — это такая штука, которая связывает одни числа с другими числами. Давай я поставлю пример. Есть функция, которая возвращает квадрат числа. Ты даешь ей число, а она возвращает его квадрат. Звучит логично, правда?
Обычно, когда ты говоришь о функции, ты говоришь о двух вещах: области определения и области значений. Область определения — это все числа, которые можно подставить в функцию. Например, функция, которую я описал выше, может принимать любое число. А область значений — это все числа, которые функция может вернуть. В нашем случае, это все квадраты чисел.
Так что вот, теперь ты знаешь что такое функция. Это просто способ связать числа друг с другом. Прикольно, правда? Теперь давай подумаем, для каких других задач можно использовать функции… и какой функцией ты бы хотел быть, если бы был математической функцией? 😉
Примеры функций
Пример 1: Функция «Умножение»
Базовым примером функции является умножение. Она принимает два числа — множители — и возвращает их произведение. Например, функция «умножение» принимает числа 2 и 3 и возвращает число 6, так как 2 * 3 = 6. Это является примером одной функции, где каждое число является элементом множества входных данных, а их произведение — элементом множества выходных данных.
Пример 2: Функция «Квадратный корень»
Еще одним примером функции является извлечение квадратного корня. Эта функция принимает число и возвращает его квадратный корень. Например, функция «квадратный корень» принимает число 9 и возвращает 3, так как √9 = 3. Здесь число 9 — элемент множества входных данных, а его квадратный корень — элемент множества выходных данных.
Пример 3: Функция «Абсолютное значение»
Функция «абсолютное значение» принимает число и возвращает его модуль, то есть значение без учета знака. Например, функция «абсолютное значение» принимает число -5 и возвращает 5, так как |-5| = 5. В этом примере число -5 — элемент множества входных данных, а его модуль — элемент множества выходных данных.
Примеры функций можно найти повсюду — в математике, программировании, физике и других областях нашей жизни. Функции позволяют нам описывать и понимать взаимосвязи между различными величинами и явлениями.
Область определения
Когда мы говорим об области определения функции, мы обращаемся к вопросу, какие значения могут принимать входные параметры функции. В простых словах, это все возможные значения, которые можно подставить в функцию и получить результат.
Область определения функции может быть ограничена различными факторами, такими как математические операции, возможные значения переменных или другие условия. Например, если у нас есть функция, которая определяет площадь прямоугольника, область определения будет ограничена положительными значениями длины и ширины прямоугольника. В противном случае, если мы подадим отрицательное значение входного параметра, функция не сможет вычислить площадь.
Понимание области определения функции важно, потому что оно позволяет нам ограничивать входные данные, с которыми мы работаем, чтобы избежать ошибок и неопределенностей. Таким образом, область определения функции помогает нам понять, какие значения можно использовать в функции и какие результаты мы можем ожидать.
Определение области определения
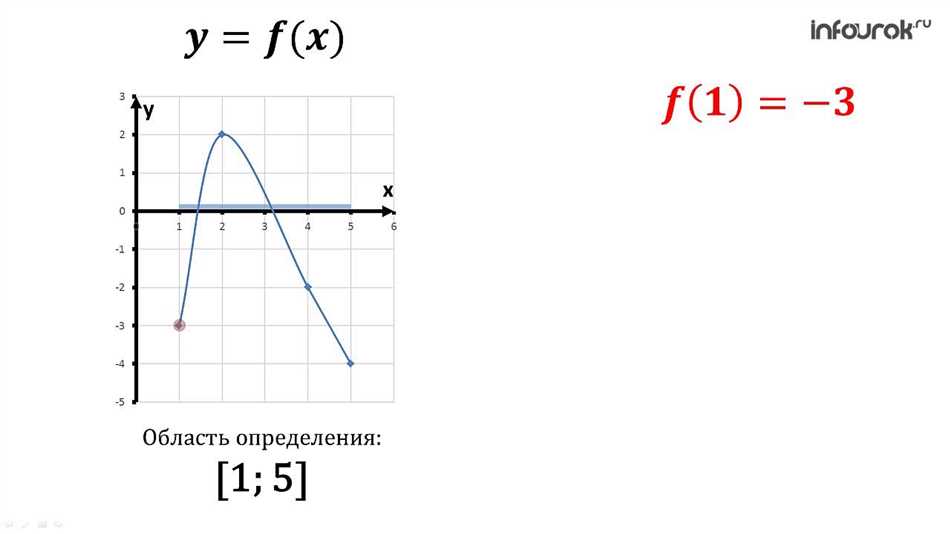
Ты когда-нибудь задумывался о том, что именно означает область определения функции? Не волнуйся, я расскажу тебе об этом в простых словах.
Область определения — это набор всех возможных значений, которые функция может принимать. Давай рассмотрим пример: у нас есть функция, которая принимает на вход число и возвращает его квадрат. В данном случае, область определения будет состоять из всех действительных чисел, так как мы можем подставить любое число в функцию и получить результат.
Однако, в некоторых случаях, область определения может быть ограничена. Например, если у нас есть функция, которая принимает на вход число и возвращает его обратное значение, то область определения будет состоять из всех чисел, кроме нуля. Почему? Потому что нуль делить нельзя, и в этом случае функция не имеет смысла.
Так что область определения — это важный аспект функции, который определяет, какие значения можно подставлять в неё. Понимание этого понятия поможет тебе лучше разбираться в математике и решать различные задачи.
Как найти область определения?
Чтобы найти область определения, нужно обратить внимание на такие факторы, как:
- Знаменатели в функции: если в функции есть дробь, то нужно исключить значения аргумента, при которых знаменатель равен нулю.
- Квадратные корни: если в функции есть квадратный корень, то нужно исключить значения аргумента, при которых подкоренное выражение меньше нуля.
- Логарифмы: если в функции есть логарифм, то нужно исключить значения аргумента, при которых логарифм равен или меньше нуля.
Иногда область определения может быть ограничена, например, для функции с обратным тригонометрическими функциями. Тогда нужно учитывать ограничения, связанные с областью определения этих функций.
Важно помнить, что область определения может быть представлена в виде интервалов, неравенств или множества чисел. Также обратите внимание на особые случаи, которые должны быть учтены при поиске области определения, например, деление на ноль.
Область значений
Разберемся, что такое область значений функции, и сделаем это простыми словами. Итак, представь себе следующую ситуацию: ты организуешь вечеринку и хочешь пригласить своих друзей. Но важно помнить, что у каждого человека есть свои предпочтения, и они могут варьироваться от того, что им нравится делать в свободное время, до того, что они любят есть.
Вот и область значений функции работает похожим образом. Она представляет собой набор всех возможных значений, которые функция может принимать. Рассмотрим пример: функция, которая описывает температуру в течение дня. Значения этой функции могут быть любыми числами, которые представляют собой температуру. Например, утром она может быть 10 градусов Цельсия, а днем – 25 градусов. Таким образом, область значений функции в данном случае будет состоять из всех возможных температур в течение дня.
Определение области значений
Давай представим себе функцию, которая описывает зависимость температуры от времени в течение дня. В нашем случае, область значения функции будет состоять из всех возможных значений температуры — от самого низкого значения до самого высокого. Мы можем получить различные значения, например, 20 градусов, 25 градусов, 30 градусов и т.д.
Область значений является важной характеристикой функции, так как она определяет, какие значения функции мы можем получить. Например, если область значений функции ограничена, то мы знаем, что функция может принимать только определенные значения и никакие другие. Также, область значений помогает нам понять, насколько разнообразны значения функции и какая информация она может нам предоставить.
Заключение
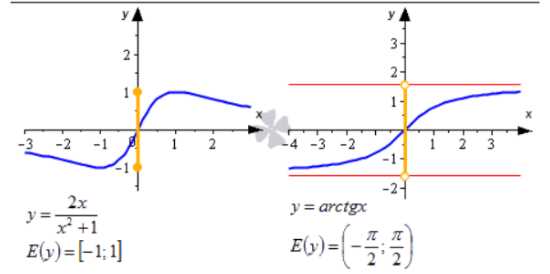
Область значений функции представляет собой множество всех возможных значений, которые может принимать функция. Она определяется исходя из области определения функции и ее правил.
Для нахождения области значений функции необходимо проанализировать ее правила и ограничения, заданные в области определения. Если функция задана аналитически, то можно использовать методы аналитической геометрии и алгебры для определения ее области значений. В случае графического представления функции, область значений можно определить, проанализировав график функции и определив множество значений, которые она принимает на оси у.
Таким образом, определение области значений функции позволяет нам узнать, какие конкретные значения может принимать функция и как ее значения зависят от области определения. Это важное понятие в математике, которое помогает нам более точно и полно описывать и анализировать функции.