Когда мы говорим о факториале числа, мы имеем в виду понятие, которое кажется сложным, но на самом деле очень простое. Факториал обозначается символом ! и обозначает произведение всех положительных целых чисел от 1 до данного числа.
Например, факториал числа 5 (обозначается как 5!) равен произведению 5 * 4 * 3 * 2 * 1, то есть 120. Это означает, что если мы возьмем пять разных предметов и упорядочим их, то у нас будет 120 возможных способов расположения.
Факториалы используются в различных областях математики, физики и информатики. Они помогают в решении задач комбинаторики и вероятности, а также в анализе сложности алгоритмов.
Итак, факториал числа — это просто произведение всех положительных целых чисел от 1 до данного числа. Каждый раз, когда вы сталкиваетесь с факториалом, помните, что это простая, но очень мощная идея, которая может быть полезна в решении различных математических задач.
Определение факториала числа
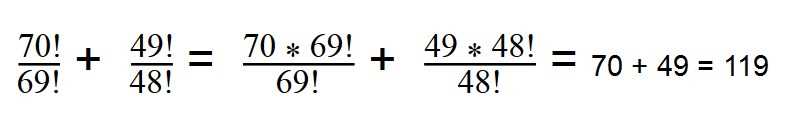
Но это довольно полезное понятие во многих областях. Например, факториалы используются в комбинаторике, когда нужно посчитать количество всевозможных перестановок или сочетаний, или в теории вероятностей, когда рассматриваются различные исходы случайных событий.
Запомни, когда говорят «факториал 5», то имеют в виду 5! (читается «пять факториал») и получается результат, равный произведению всех чисел от 1 до 5: 1 * 2 * 3 * 4 * 5 = 120. Круто, правда?
А еще, обрати внимание, что факториал 0 равен 1, потому что существует только один способ умножить ничего — это ничего не делать.
Математическое понятие факториала
Вот как она работает: если у нас есть положительное целое число, скажем, 5, то его факториал обозначается как 5! И что же означает символ «!» здесь? Он не означает, что число «кричит» или проявляет эмоции, не беспокойся.
Символ «!» в математике означает умножение всех положительных целых чисел от 1 до данного числа. Таким образом, 5! равно 5 * 4 * 3 * 2 * 1, что равняется 120. Просто впечатляюще, правда?
Так что факториал — это способ найти произведение всех чисел от 1 до заданного числа. Он часто используется в комбинаторике и математическом анализе для решения различных задач. Например, можно использовать факториал для рассчета числа возможных перестановок или комбинаций элементов.
И это еще не все! Факториал также имеет свои свойства и интересные связи с другими математическими концепциями, такими как биномиальные коэффициенты и числа Каталана. Математика — это удивительная вещь, верно?
Так что вот, теперь у тебя есть лучшее понимание того, что такое факториал. Это всего лишь операция, которая умножает все положительные целые числа от 1 до заданного числа. Надеюсь, теперь ты чувствуешь себя немного математическим гуру! Удачи в дальнейших математических подвигах!
Обозначение и вычисление факториала

Добро пожаловать в увлекательный мир математики! Сегодня мы поговорим о факториале числа. Итак, что же такое факториал?
Факториал числа обозначается символом «!». Например, если мы хотим вычислить факториал числа 5, то пишем «5!». Это означает, что нужно перемножить все натуральные числа от 1 до 5 включительно: 1 * 2 * 3 * 4 * 5. Результатом будет число, называемое факториалом.
Вычисление факториала может быть довольно интересным и полезным процессом. Оно находит свое применение в различных областях, например, в комбинаторике и анализе алгоритмов.
Для вычисления факториала числа есть два основных подхода. Первый подход — это прямое вычисление, когда мы последовательно умножаем все числа от 1 до данного числа. Например, чтобы вычислить факториал числа 5, мы начинаем с 1 и умножаем его на 2, затем результат умножаем на 3 и так далее, пока не получим факториал. Результат — 120.
Второй подход — это использование рекурсии. Мы можем определить функцию, которая будет вызывать саму себя с аргументом, уменьшенным на 1. Когда аргумент становится равным 1, мы прекращаем вызов и возвращаем значение 1. Например, чтобы вычислить факториал числа 5, мы вызываем функцию, передавая ей аргумент 5. Функция вызывает саму себя с аргументом 4, затем с аргументом 3 и так далее, пока не вызовет себя с аргументом 1. Затем функция возвращает 1, и мы перемножаем все возвращенные значения для получения факториала. Результат также будет 120.
Таким образом, факториал числа — это произведение всех натуральных чисел от 1 до данного числа. Его можно вычислять как прямым методом, последовательно умножая числа, или с помощью рекурсии. Попробуйте вычислить факториалы разных чисел и посмотрите, какой подход вам больше нравится!
Примеры вычисления факториала
1. Начнем с простого примера. Вычислим факториал числа 4. Для этого надо перемножить все числа от 1 до 4: 1 * 2 * 3 * 4 = 24. Таким образом, факториал 4 равен 24.
2. Теперь рассмотрим более сложный пример. Вычислим факториал числа 6. Умножаем все числа от 1 до 6: 1 * 2 * 3 * 4 * 5 * 6 = 720. Получаем, что факториал 6 равен 720.
3. Не существует отрицательного факториала. Например, факториал числа -5 неопределен, так как нельзя перемножить все натуральные числа от 1 до -5.
4. Факториал нуля равен единице. Почему? Потому что умножение на единицу не меняет значение числа, поэтому 0! = 1.
5. Важно помнить, что факториал растет очень быстро. Например, факториал числа 10 равен 3 628 800. А факториал числа 20 уже составляет 2 432 902 008 176 640 000!
Таким образом, факториал числа — это уникальное математическое понятие, которое используется в различных областях, включая комбинаторику, статистику и теорию вероятностей. Вычисление факториала позволяет нам решать разнообразные задачи и находить вероятности, перестановки, сочетания и многое другое. Важно понимать, что факториал — это мощный инструмент, который может быть использован для решения различных задач в реальном мире.
Примеры вычисления факториала малых чисел
Давайте посмотрим на несколько примеров вычисления факториала для малых чисел:
- 1! = 1, потому что не существует никаких чисел, которые нужно перемножить.
- 2! = 2 * 1 = 2, потому что умножаем все натуральные числа от 1 до 2.
- 3! = 3 * 2 * 1 = 6.
- 4! = 4 * 3 * 2 * 1 = 24.
- 5! = 5 * 4 * 3 * 2 * 1 = 120.
Факториал числа 0 тоже существует, и он равен 1. Это может показаться странным, но если мы рассмотрим определение факториала, то поймем, что перемножение натуральных чисел от 1 до 0 невозможно, поэтому принято считать, что 0! = 1.
Вычисление факториала — это простой способ найти количество возможных перестановок или комбинаций элементов в математике и комбинаторике. Он также широко используется в различных научных и инженерных расчетах. Попробуйте сами посчитать факториалы для других малых чисел — это отличное упражнение для тренировки вашей математической интуиции и навыков!
Пример вычисления факториала большего числа
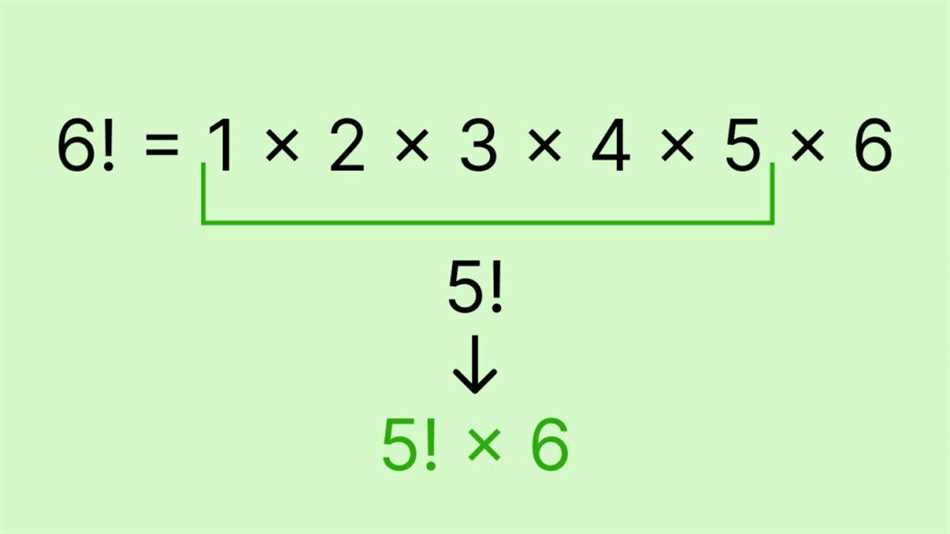
Давайте рассмотрим пример вычисления факториала для большего числа, такого как 10. Факториал числа обозначает произведение всех положительных целых чисел, начиная с 1 и заканчивая заданным числом. То есть факториал 10 обозначается как 10! и равен 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1.
Итак, нам нужно вычислить произведение всех чисел от 1 до 10. Давайте начнем:
- У нас есть число 1. Умножаем его на 2, получаем 2.
- Умножаем 2 на 3, получаем 6.
- Умножаем 6 на 4, получаем 24.
- Умножаем 24 на 5, получаем 120.
- Умножаем 120 на 6, получаем 720.
- Умножаем 720 на 7, получаем 5040.
- Умножаем 5040 на 8, получаем 40320.
- Умножаем 40320 на 9, получаем 362880.
- Наконец, умножаем 362880 на 10 и получаем результат: 3,628,800.
Таким образом, факториал числа 10 равен 3,628,800.
Интересно, правда? Факториалы используются в различных областях, например, в комбинаторике и вычислительной математике. Знание того, как вычислять факториалы больших чисел, может быть очень полезным. Попробуйте самостоятельно вычислить факториал для других чисел и увидите, как быстро они растут!