Инъекция в математике – это понятие, которое имеет отношение к функциям и отображениям между множествами. Конкретно, инъекция обозначает, что каждому элементу из исходного множества соответствует уникальный элемент в целевом множестве. То есть, каждому x в исходном множестве соответствует единственный y в целевом множестве, и никакие другие элементы в целевом множестве не имеют такого же соответствия.
Инъекция также называется однонаправленным отображением, так как каждому элементу в исходном множестве соответствует только один элемент в целевом множестве. Инъекция важна в математике и ее применяют в различных областях, включая алгебру, теорию множеств, и дискретную математику.
Инъекция играет важную роль при определении биекции, сюръекции и других понятий, связанных с функциями и отображениями между множествами. Она позволяет создавать связи между элементами множеств без потери информации и является основой для решения различных задач в математике и других науках.
Инъекция в математике
Что такое инъекция? Представьте, что у вас есть две группы людей: группа A и группа B. И инъекция — это способ связать каждого человека в группе A с уникальным человеком в группе B. Никто из группы A не может быть связан с двумя или более людьми в группе B. Это как некий «математический диктатор», который гарантирует, что каждый человек из группы A будет иметь своего соответствующего партнера в группе B.
Интересно, правда? Но зачем нам это? Ответ прост: инъекции помогают нам анализировать и классифицировать различные связи и отношения между объектами. Они помогают нам понять, как одни объекты связаны с другими, и как эти связи можно организовать. В математике инъекции используются для изучения функций и множеств, и они играют ключевую роль в теории чисел, алгебре и других областях.
Теперь, когда вы знаете о инъекциях, вы можете почувствовать себя немного ближе к миру математики. Это всего лишь один маленький шаг, но он может открыть вам двери к новым знаниям и возможностям. Так что не бойтесь математики, ведь она может быть дружественной и захватывающей, как инъекции в математике!
Определение инъекции
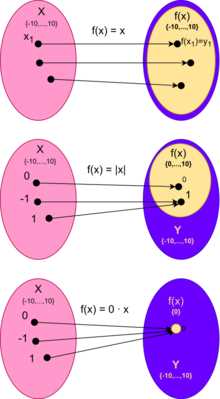
Давай посмотрим на простой пример. Представьте, что у нас есть множество студентов и множество их идентификационных номеров. Если для каждого студента выделен только один уникальный идентификационный номер, и мы можем присвоить каждому студенту только один номер, то мы имеем инъекцию.
Важно отметить, что инъекция не требует, чтобы каждый элемент в выходном множестве имел соответствие во входном множестве. То есть, в выходном множестве могут быть элементы, которые не имеют отображения во входном множестве. Главное требование для инъекции состоит в том, что каждый элемент во входном множестве имеет уникальное отображение в выходном множестве.
Примеры инъекций
Давайте рассмотрим несколько примеров инъекций:
-
Инъекция натуральных чисел в целые числа: Функция f(n) = n является инъекцией, так как каждое натуральное число будет отображаться только на себя в множестве целых чисел. Ни одно число не будет отображено на два или более числа.
-
Инъекция маленьких букв английского алфавита в большие буквы: Функция f(x) = x, где x — маленькая буква английского алфавита, является инъекцией, так как каждая маленькая буква будет отображаться только на себя в множестве больших букв. Ни одна маленькая буква не будет отображена на две или более больших буквы.
-
Инъекция точек на плоскости в области неограниченного размера: Функция f(x, y) = (x, y), где (x, y) — точка на плоскости, является инъекцией, так как каждая точка будет отображаться только на себя в области неограниченного размера. Ни одна точка не будет отображена на две или более точки.
Инъекции имеют важное значение в математике и других областях науки, так как они позволяют нам строить отношения между разными множествами, сохраняя каждый элемент уникальным и не повторяющимся.
Важность абстракции в инъекциях
Представьте себе, что вы играете в игру с друзьями, и вы хотите показать им свои навыки в инъекциях. Вам нужно выбрать правильную стратегию, чтобы успешно сделать свой ход и выиграть игру. Точно так же и в математике, абстракция играет важную роль в инъекциях.
Абстракция позволяет нам сосредоточиться на сути проблемы, игнорируя ненужные детали. В контексте инъекций, абстракция помогает нам понять, как одно множество отображается в другое, без необходимости рассматривать конкретные элементы этих множеств.
Необходимость абстракции становится особенно явной в сложных математических концепциях. Например, при изучении функций или множеств, мы можем сократить количество информации и сосредоточиться только на основных свойствах и отношениях между элементами. Это позволяет легче понять и применять инъекции в различных областях математики и науки в целом.
Также, абстракция помогает нам обобщать знания и создавать универсальные принципы на основе конкретных случаев. Это позволяет нам применять изученные концепции в новых ситуациях и находить решения для разных типов задач. В итоге, абстракция позволяет нам расширять наши познания и создавать новые инновационные идеи.
В заключении, абстракция играет важную роль в инъекциях, помогая нам сосредоточиться на сути проблемы и создавать универсальные концепции. Она помогает нам понять инъекции в математике и применять эти знания в широком спектре областей. Идите и наслаждайтесь абстракцией!
Инъекции в компьютерных науках
Инъекции также могут быть использованы для обхода системных ограничений и получения привилегий. Например, веб-инъекции могут использоваться для выполнения удаленного кода на сервере и получения полного контроля над системой. Кроме того, инъекции могут быть использованы для проведения фишинговых атак или распространения вредоносного программного обеспечения.
Для предотвращения инъекций в компьютерных науках необходимо применять соответствующие техники безопасности, такие как фильтрация и валидация ввода данных, использование подготовленных запросов в базе данных и ограничение доступа к системным ресурсам. Кроме того, важно регулярно обновлять и патчить программное обеспечение, чтобы устранить известные уязвимости.
Отношение инъекции к другим математическим понятиям
Во-первых, инъекция является одним из средств для определения биекции – отображения, при котором каждый элемент из одного множества соответствует только одному элементу из другого множества, и наоборот. Если отображение одновременно является инъекцией и сюръекцией (также называется биекцией), то оно устанавливает однозначное соответствие между множествами.
Во-вторых, инъекция находит применение при рассмотрении функций, которые сохраняют определенные свойства объектов. Например, функция может быть инъективной, если каждое значение второго множества соответствует только одному значению из первого множества. Такие функции позволяют лучше понять зависимости и взаимосвязи между объектами.
Наконец, инъекция также связана с понятием «мощность». Если существует инъективное отображение множества A в множество B, то мощность множества A меньше или равна мощности множества B. Это важное свойство позволяет сравнивать размеры множеств и классифицировать их по количеству элементов.
Таким образом, инъекция является важным понятием в математике, которое имеет отношение к другим понятиям, таким как биекция, функция и мощность множества. Рассмотрение и изучение этих связей позволяют лучше понять и использовать инъекции в решении математических задач.
Практическое применение инъекций

Одним из основных применений инъекций является моделирование процессов и взаимодействий в реальном мире. Например, в физике и инженерии инъекции используются для описания движения твёрдых тел, распространения электромагнитных волн, теплообмена и других физических явлений. В экономике инъекции позволяют моделировать процессы производства, потребления и рыночных взаимодействий.
Также инъекции применяются в статистике и анализе данных для описания и классификации наблюдаемых явлений. Инъекции позволяют устанавливать соответствия между различными переменными и строить модели, позволяющие предсказывать и объяснять различные связи и закономерности.
В машинном обучении и искусственном интеллекте инъекции используются для создания алгоритмов распознавания образов, голоса, текста и других типов данных, а также для построения моделей принятия решений и оптимизации процессов.
- Инъекции обладают высокой гибкостью и адаптивностью к различным задачам и условиям.
- Они позволяют применять универсальные методы и подходы для анализа и решения сложных проблем.
- Инъекции являются основой для развития новых методов и технологий.
Таким образом, практическое применение инъекций в математике раскрывает большое количество возможностей для моделирования и анализа различных явлений и процессов, приводя их к удобным формулам и моделям. Это позволяет получать более точные и полезные результаты, упрощает и автоматизирует процесс принятия решений и оптимизации, а также способствует развитию науки и технологий в целом.



