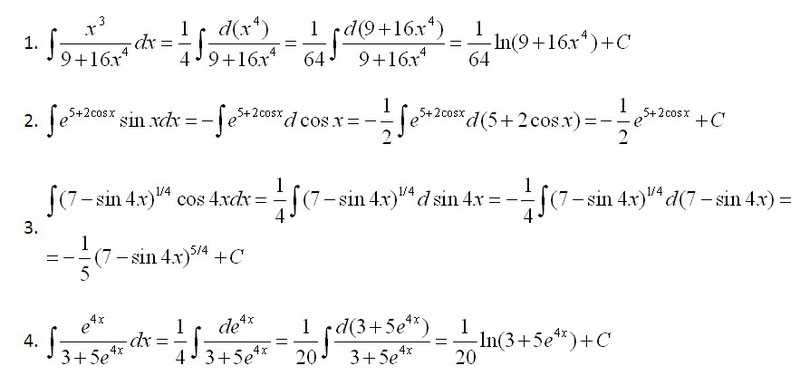
Интеграл — это мощный инструмент в математике, который позволяет решать различные задачи, связанные с площадями, объемами, скоростью изменения функций и многими другими. Представьте себе, что интеграл — это как волшебная кнопка, которая помогает найти ответ на интересующий вопрос.
Чтобы понять, что такое интеграл, давайте приведем простой пример. Представьте, что у вас есть график функции, который показывает зависимость скорости движения автомобиля от времени. Возможно, вам будет интересно узнать, какое расстояние автомобиль проедет за определенный промежуток времени.
Здесь на помощь приходит интеграл. Он позволяет найти площадь под графиком функции, то есть расстояние, пройденное автомобилем за указанный промежуток времени. Это всего лишь один из множества примеров использования интеграла, который может быть полезен как в решении реальных задач, так и в самой математике.
Интеграл в математике для чайников
Интеграл — это как крошечные строительные блоки, с помощью которых мы можем собрать большую и красивую картину. Он помогает нам найти площадь, обьем, а иногда даже скорость и количественные характеристики величин.
Представь себе, что ты готовишь пиццу. Твоя задача — высчитать, сколько ты потратишь времени на это веселье. Интеграл поможет тебе. Ты можешь разбить время на крошечные части: первую минуту, вторую минуту, и так далее. Время каждой части будет немного отличаться — первая минута может быть очень спокойной, а вторая — увлекательной. Ты можешь учесть все эти различия, сложить их вместе и получить общую сумму — именно это и есть интеграл!
Та же самая логика работает и в математике. Мы разбиваем область на маленькие части, вычисляем площадь каждой части и собираем их все вместе, чтобы получить общую площадь. Интеграл это и есть этот процесс сборки!
И вот, таким образом, интеграл становится нашим верным помощником в математике. Не бойся его, попробуй использовать его, и ты увидишь, как просто и удивительно можно решать задачи с его помощью!
Определение интеграла
Интеграл — это способ измерить площадь под кривой. Допустим, у тебя есть график, который показывает, как меняется какая-то величина в зависимости от другой величины. Интеграл позволяет определить точное значение площади под этим графиком.
Прежде всего, для вычисления интеграла необходимо разделить график на бесконечно маленькие прямоугольники и найти площадь каждого из них. Затем все эти маленькие площади складываются вместе, и получается площадь под всей кривой.
Итак, интеграл — это просто способ найти площадь под кривой. Но на самом деле это является основополагающим понятием в математике и имеет обширное применение в науке и технике. Ведь многие величины, например, скорость, площадь, объем, взаимосвязаны исследованием площадей под кривыми. Это одно из удивительных свойств математики — она позволяет нам измерять и понимать мир вокруг нас.
Применение интеграла
Механика
Интегралы используются для решения различных задач в механике. Например, они позволяют найти путь, пройденный телом при заданной силе, или определить работу силы, действующей на тело.
Физика
В физике интегралы помогают решать задачи связанные с определением площади под кривой в графике зависимости различных физических величин.
Экономика
Интегралы значительно упрощают анализ и моделирование экономических процессов. Например, с помощью интегралов можно определить доход, затраты и прибыль предприятия.
Статистика и вероятность
Интегралы применяются в статистике и теории вероятности для определения вероятности события, площади под графиком или функцией распределения.
Исследование
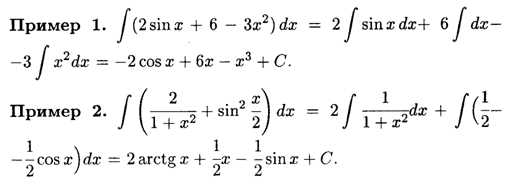
В научных исследованиях интегралы используются для анализа данных, моделирования процессов и определения закономерностей. Они позволяют установить определенные зависимости и предсказать результаты эксперимента.
И это только несколько областей, в которых интегралы применяются. Их применение может быть неограниченным, в зависимости от задачи, которую необходимо решить. Следовательно, понимание и умение работать с интегралами крайне важны для прогресса в науке и технике. Ведь они помогают нам лучше понимать окружающий мир и решать сложные задачи.
Методы вычисления интеграла

Итак, вы хотите узнать, как вычислять интегралы, не так ли? Существует несколько методов для решения этой задачи, и сегодня я расскажу вам о некоторых из них.
Первый метод, о котором я хочу поговорить, называется аналитическим. Он основан на использовании формулы интегрирования и правил дифференцирования, таких как правило замены и правило интегрирования по частям. С помощью этого метода можно найти точное значение интеграла.
Однако иногда аналитическое решение интеграла может быть сложным или даже невозможным. В таких случаях можно воспользоваться численными методами. Один из самых простых численных методов — метод прямоугольников. Он заключается в том, что мы разделяем область под графиком функции на прямоугольники и приближаем площадь каждого прямоугольника с помощью его высоты. Чем больше прямоугольников мы используем, тем точнее будет приближение.
Еще одним численным методом вычисления интеграла является метод тrapezoid, или метод трапеций. Он похож на метод прямоугольников, но вместо прямоугольников мы используем трапеции. Таким образом, мы улучшаем приближение, так как трапеции лучше аппроксимируют форму под графиком функции.
Если вы хотите более точное приближение, то можете воспользоваться методом Симпсона. Он основан на аппроксимации функции параболой и дает более точный результат. Для вычисления интеграла с помощью этого метода мы разбиваем область под графиком функции на прямоугольники, а затем аппроксимируем каждый прямоугольник параболой. Таким образом, мы получаем более точное значение интеграла.
Исходя из этого, вы можете видеть, что существует несколько методов вычисления интеграла, и выбор зависит от сложности задачи и требуемой точности. Надеюсь, что это руководство поможет вам начать изучение этой интересной и полезной математической темы!
Геометрическая интерпретация интеграла
При геометрической интерпретации интеграла мы рассматриваем функцию как график, а интегрирование сводится к нахождению площади ограниченной области под графиком функции. Если функция положительна на заданном интервале, то интеграл будет представлять собой площадь фигуры, заключенной между графиком функции и осью абсцисс.
Интеграл также может быть использован для определения объема тела, полученного вращением кривой вокруг оси абсцисс или оси ординат. В этом случае интеграл представляет собой объемной пространство, занимаемое вращающейся кривой.
Геометрическая интерпретация интеграла позволяет увидеть связь между математическими выражениями и реальными геометрическими объектами. Она помогает лучше понять смысл и назначение интеграла в математике и его применение в решении различных практических задач.