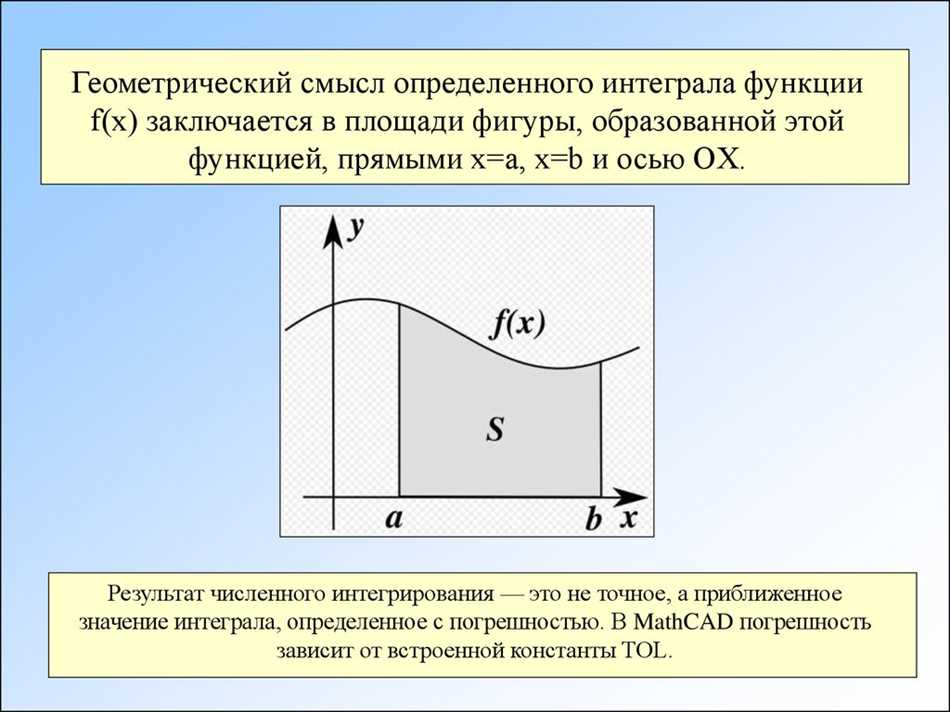
Интегрирование и дифференцирование — это две основных операции в математическом анализе, которые позволяют нам изучать свойства и поведение функций. Дифференцирование позволяет нам найти производную функции — ее тангенс угла наклона в каждой точке, а интегрирование дает нам интеграл функции — площадь под кривой.
Интегрирование и дифференцирование тесно связаны друг с другом — вычисление производной исходной функции позволяет нам найти интеграл этой функции и наоборот. Через эти две операции математика и физика находят ответы на множество вопросов и решают разнообразные задачи.
Дифференцирование и интегрирование являются незаменимыми инструментами в различных областях науки и техники, а также на практике, в решении задач из реального мира. Они помогают нам понять и предсказать различные явления и функции, и открывают перед нами новые возможности в исследовании и управлении природными и техническими процессами.
Определение и основные понятия
Так вот, интегрирование — это процесс нахождения интеграла от функции. Интеграл — это величина, которая обозначает площадь под графиком функции. То есть, когда мы интегрируем, мы ищем сумму всех маленьких площадок, которые складываются в одну большую область.
А дифференцирование наоборот, это процесс нахождения производной от функции. Производная — это скорость изменения функции в каждой ее точке. Как будто мы смотрим, насколько быстро функция меняется, когда аргумент меняется. Как ты думаешь, зачем нам знать скорость изменения функции? Да потому что это помогает нам решить множество задач! Например, определить точку максимума или минимума функции.
Так, я хочу подчеркнуть, что интегрирование и дифференцирование — это взаимосвязанные процессы. Интеграл и производная — это две стороны одной медали. Интеграл позволяет найти функцию, зная ее производную, а дифференциал позволяет найти производную функции, зная ее интеграл.
Таким образом, интегрирование и дифференцирование — это мощные инструменты, которые находят свое применение во многих областях науки и техники. Они позволяют нам анализировать и понимать сложные функции, а также находить решения задач, которые ранее казались неразрешимыми. Вот такие вот удивительные возможности математики!
Интегрирование: универсальный инструмент математики
Интегрирование — это процесс, который обратен дифференцированию. Ты, наверное, знаком с дифференцированием — это когда мы находим производную функции. Интегрирование, с другой стороны, позволяет найти первообразную функции.
Представь себе график функции на координатной плоскости. Если ты хочешь узнать, какая площадь находится под графиком между двумя точками, то тебе понадобится интегрирование. Это как будто ты «суммируешь» значения функции на каждом кусочке графика и получаешь общую сумму. Интеграл функции на отрезке обозначается как ∫(integral) от a до b (a и b — границы отрезка).
Интегрирование также применяется для нахождения объемов тел в пространстве и многих других задач. Оно помогает понять, как меняется функция в зависимости от переменной и класть основу для многих областей науки и техники.
Так что, интегрирование — это один из фундаментальных инструментов математики, позволяющий решать широкий спектр задач. Не забывай об этом при следующей учебе математике или при решении реальных задач!
Дифференцирование

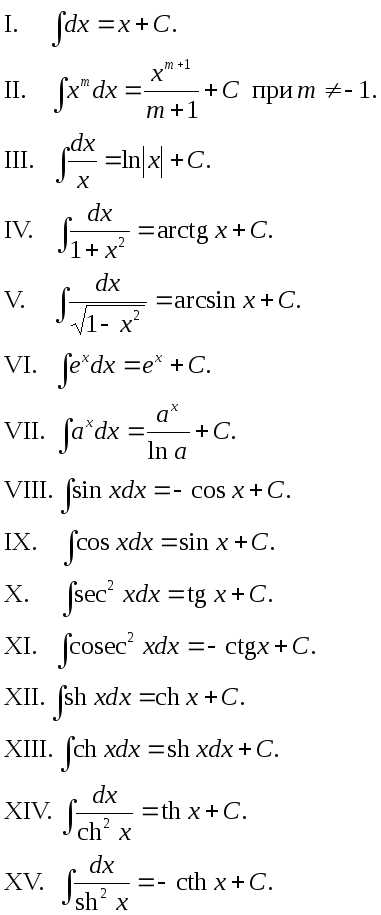
Дифференцирование — это как найти тангенс к графику — скорость роста функции в каждой точке. Если простыми словами, то это позволяет нам понять, насколько быстро функция меняется в какой-то точке.
Все звучит сложно, не так ли? Но на самом деле дифференцирование — это очень мощный инструмент, который позволяет нам решать различные задачи. Например, мы можем использовать дифференцирование для нахождения максимумов и минимумов функций, для понимания формы графиков и еще многих других вещей.
Основная идея дифференцирования заключается в том, что мы берем функцию и находим ее производную. Производная — это функция, которая показывает нам скорость роста и изменение исходной функции. Таким образом, дифференцирование позволяет нам получить полезную информацию о функции, которую мы можем использовать для анализа и решения задач.
Итак, дифференцирование — это ключевой инструмент в математике, который помогает нам изучать и анализировать изменение функций. Оно позволяет нам понять, как функции меняются в разных точках и как они взаимодействуют друг с другом. Поэтому не стесняйтесь использовать дифференцирование в своих математических исследованиях — это мощное оружие, которое поможет вам получить новые знания и ощутимые результаты!
Применение в математике
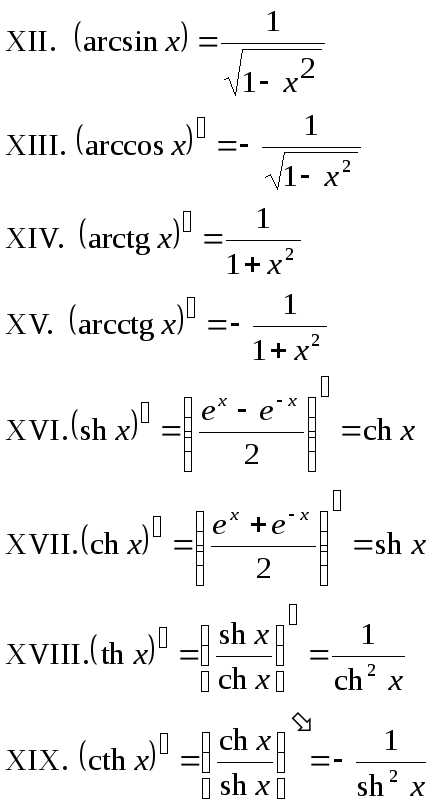
Теперь, когда мы знаем, что такое интегрирование и дифференцирование, давайте посмотрим, как они применяются в математике.
Начнем с дифференцирования. Оно позволяет нам находить производные функций. Это особенно полезно, когда нам нужно понять, как изменяется функция в разных точках. Например, мы можем использовать дифференцирование, чтобы определить скорость изменения популяции животных в какой-то конкретный момент времени.
Интегрирование, с другой стороны, позволяет нам находить площадь под кривой. Мы можем использовать интегрирование для нахождения площади огороженной земли или площади под графиком зависимости.
Кроме того, интегрирование и дифференцирование помогают нам решать дифференциальные уравнения, которые встречаются во многих областях, включая физику, экономику и инженерию. Они позволяют нам анализировать изменения, прогнозировать будущие события и оптимизировать процессы.
В общем, интегрирование и дифференцирование — это мощные математические инструменты, которые помогают нам понять и описать мир вокруг нас. Они позволяют нам исследовать сложные взаимосвязи и строить модели, которые помогают принимать решения и предсказывать результаты. И все это благодаря двум простым, но очень важным операциям: интегрированию и дифференцированию.
Интегрирование
Интегрирование решает эти вопросы! Оно позволяет нам найти площадь под кривой графика функции. Вот как это работает: мы берем нашу функцию и разбиваем ее на бесконечно маленькие кусочки, каждый из которых мы можем приблизить прямоугольником. Затем мы складываем площади всех этих прямоугольников и получаем общую площадь под кривой.
Такая процедура называется определенным интегралом. Он обозначается знаком ∫ (интеграл) и выглядит, например, так: ∫ f(x) dx, где f(x) – наша функция, а dx – маленькое изменение x. Результат интегрирования – это новая функция, которую мы называем первообразной. Она описывает общую площадь под кривой и переводит нашу исходную функцию в новую форму.
Дифференцирование
Здравствуйте! Сегодня я хотел бы поговорить с вами о дифференцировании, одном из основных понятий в математике. Наверное, большинство из вас уже слышали об этом термине, но давайте вспомним, что он означает и почему он так важен.
Дифференцирование — это процесс нахождения производной функции. А что такое производная? Давайте представим, что у нас есть функция, которая описывает зависимость какой-то величины от другой. Производная этой функции показывает, какая будет скорость изменения этой величины в каждой точке. Это может быть полезно в различных ситуациях, например, при решении задач по физике, экономике или инженерии.
Чтобы найти производную функции, нужно использовать определенные правила и формулы. Это может показаться сложным на первый взгляд, но со временем вы поймете, что это всего лишь набор инструментов, который помогает разобраться в сложных математических задачах. Не бойтесь экспериментировать и задавать вопросы. Не стесняйтесь обратиться к учителям или сокурсникам за помощью, если что-то не понятно.
Дифференцирование — это увлекательный и мощный инструмент, который может помочь вам лучше понять мир вокруг нас. Математика велика своей способностью моделировать и объяснять реальность, и дифференцирование является одним из ключей к этому пониманию. Итак, давайте погружаться в мир дифференцирования и открывать новые горизонты знаний!
Применение интегрирования и дифференцирования в физике
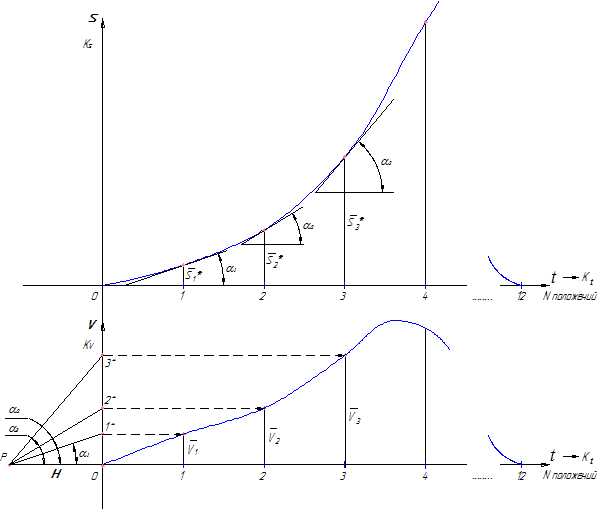
Рассмотрим, например, применение дифференцирования. Дифференцирование позволяет нам найти скорость изменения физической величины по отношению к другой величине. Оно используется для нахождения скоростей, ускорений и многих других важных параметров. Например, чтобы узнать скорость движения тела в данный момент времени, мы может продифференцировать его путь по времени.
С другой стороны, интегрирование позволяет нам найти общую сумму некоторой физической величины на протяжении определенного интервала. Например, мы можем использовать интегрирование для определения пути, пройденного телом, на основе его скорости в каждый момент времени. Также интегрирование применяется для определения массы, плотности и других физических параметров.
Таким образом, интегрирование и дифференцирование являются мощными инструментами в физике, которые позволяют нам анализировать и моделировать различные физические явления и процессы. Они помогают нам понять, как работает мир вокруг нас и развивают наше понимание фундаментальных законов природы. Знание этих математических операций может быть полезным для студентов и исследователей во многих областях физики, таких как механика, электродинамика, квантовая физика и другие.
Интегрирование
Знаешь, что есть несколько способов интегрирования? Один из них — метод интегрирования по частям. Он позволяет разложить сложную функцию на две более простые, чтобы потом было легче их проинтегрировать. Также есть метод замены переменной, когда мы меняем одну переменную на другую, чтобы упростить задачу. Интересно, правда?
Так что, интегрирование — это как путешествие в мир математики, где каждая функция и каждая задача ждут своего решения. Будешь искать функции, находить площади и объемы, применять интегрирование в физике и экономике. Ведь когда ты понимаешь, как работает интегрирование, мир открывает перед тобой свои тайны и секреты. А ты готов стать исследователем и познавать всю красоту математики?
Заключение:
Процесс дифференцирования основан на концепции локального изменения функции и ее тангенса к касательной линии. Оно позволяет нам анализировать скорость изменения функции в определенной точке, что является ключевым фактором для решения многих задач. Дифференцирование также помогает нам находить экстремумы функций и определять их поведение в разных точках.
Кроме того, дифференцирование является важной составляющей для более сложных математических концепций, таких как интегрирование, кратные производные и дифференциальные уравнения. Оно используется в физике для анализа движения и изменения систем, в экономике для определения эластичности спроса и предложения, а также во многих других областях.






