Что такое иррациональное число простыми словами

Иррациональные числа – это числа, которые не могут быть представлены в виде обыкновенной десятичной дроби или дроби в виде отношения двух целых чисел. Они не имеют конечного или периодического десятичного представления.

Давай рассмотрим пример. Возьмем число «пи» (π) – оно является одним из наиболее известных иррациональных чисел. Начиная с его десятичных знаков, мы увидим, что они не образуют никакой закономерности или повторяющиеся цифры. Пи – это бесконечная не периодическая десятичная дробь. В десятичной записи «пи» начинаются с 3.1415926 и продолжаются в бесконечность.

Иррациональные числа имеют важное значение в математике и науке, так как они позволяют нам описывать и моделировать некоторые явления, которые не могут быть точно представлены рациональными числами. Они проникают в различные области науки, физики, астрономии и других дисциплин.

Определение иррациональных чисел

Представь себе, что у тебя есть пирог, который ты хочешь разделить на равные части. Если ты можешь разделить его на целое число частей, то это будет рациональное число. Например, если ты разделишь пирог на 2, 4 или 10 равных частей, ты получишь рациональное число. Но если ты хочешь разделить пирог на, скажем, 3 равные части, то это будет иррациональное число.

Наиболее известным иррациональным числом является число π (пи). Он равен отношению окружности к ее диаметру и приблизительно равен 3,14. Другим примером иррационального числа является число √2 (корень из 2), которое не может быть записано в виде простой десятичной дроби и бесконечно продолжается без повторяющихся групп цифр.

Иррациональные числа встречаются во многих областях, таких как геометрия, физика и математические моделирование. Несмотря на то, что иррациональные числа не могут быть точно представлены в виде конечной десятичной дроби или отношения двух целых чисел, они играют важную роль в нашем понимании мира и помогают нам решать сложные математические проблемы.

Различие между рациональными и иррациональными числами

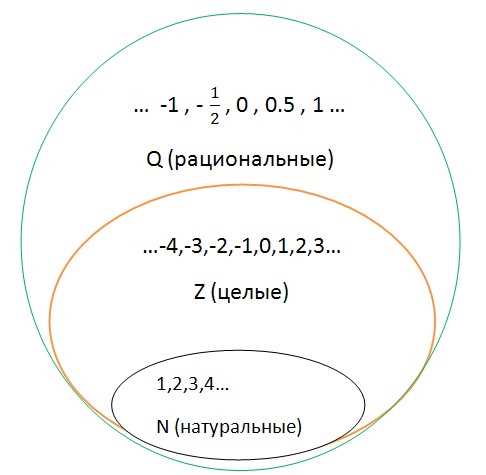
Ах, эти числа! Кажется, что их бесконечное количество, и все они уникальные. Но на самом деле числа можно разделить на две большие группы: рациональные и иррациональные.

Давай начнем с рациональных чисел. Они, знаешь ли, довольно простые. Они могут быть представлены в виде обыкновенной дроби, где числитель и знаменатель — целые числа. Например, 1/2, 3/4, или 7/1. Но есть и другие представления рациональных чисел, например, десятичные дроби, которые имеют конечный или повторяющийся шаблон.

Но у иррациональных чисел дела не так просто. Они не могут быть представлены в виде обыкновенной дроби. Они не имеют конечного или повторяющегося шаблона в десятичном представлении. Корень из двух, правда, является иррациональным числом. Он равен приблизительно 1,41421356 и так далее… Ну, ты понял идею, да? Иррациональные числа весьма необычны и загадочны.

Теперь возникает вопрос: а для чего нам нужно это знать? Это отличный вопрос, друг! Знание о том, что существуют рациональные и иррациональные числа, помогает нам понять, что некоторые величины, например, длина диагонали квадрата со стороной в единицу, невозможно представить в виде обыкновенной дроби. Это важно для геометрии и вычислений. Кроме того, это просто интересно!

И, пожалуй, отдельно стоит сказать про бесконечно малые и бесконечно большие числа. Это еще отдельная категория, которая тоже интересна, но сейчас не про нее.

Надеюсь, я смог прояснить разницу между рациональными и иррациональными числами для тебя, мой друг! Так что держи эту информацию в голове и продолжай открывать для себя удивительный мир чисел!

Примеры иррациональных чисел

Корень из двух (√2)

Один из самых известных примеров иррациональных чисел – это корень из двух (√2). На первый взгляд, может показаться, что корень из двух можно представить в виде десятичной дроби, но это не так. Значение корня из двух – это бесконечная и непериодическая десятичная дробь: 1,41421356…

Пи (π)

Еще одним примером иррационального числа является число пи (π). Пи – это отношение длины окружности к ее диаметру. Значение числа пи – это бесконечная и непериодическая десятичная дробь: 3,1415926535…

Експонента (е)

Експонента (е) – это одно из самых важных математических констант. Она используется во многих областях науки и инженерии. Значение числа е – это также бесконечная и непериодическая десятичная дробь: 2,7182818284…

Золотое сечение (φ)

Золотое сечение (φ) – это пропорция, которая часто встречается в природе и искусстве. Значение числа φ – это иррациональное число, приближенное значением 1,6180339887…

Это только некоторые из примеров иррациональных чисел. В мире математики существует еще много таких чисел, которые не могут быть представлены в виде простой десятичной или дробной десятичной дроби. Изучение и понимание иррациональных чисел играет важную роль в развитии математической мысли и углубляет наше понимание мира вокруг нас.

Доказательство иррациональности чисел

Доказательство иррациональности чисел может быть сложным и требовать математических навыков, но давайте посмотрим на один из способов понять, почему некоторые числа являются иррациональными.

Возьмем √2 в качестве примера. Предположим, что √2 является рациональным числом, то есть может быть записано в виде простой дроби вида a/b, где a и b являются целыми числами без общих делителей. Тогда мы можем записать уравнение:

√2 = a/b.

Возведем обе части этого уравнения в квадрат:

2 = (a/b)^2

2 = (a^2)/(b^2)

Перемножим обе части уравнения на b^2:

2b^2 = a^2

Получили, что a^2 — это четное число, так как 2b^2 — это четное число (ведь 2 умноженное на любое число дает четное число). Значит, a тоже должно быть четным числом.

Теперь давайте представим a в виде a = 2k, где k — целое число.

Тогда получим:

2b^2 = (2k)^2

2b^2 = 4k^2

b^2 = 2k^2

Но заметим, что b^2 также является четным числом, поэтому b тоже должно быть четным.

Мы пришли к противоречию: если a и b четные числа, то они имеют общие делители (2), что противоречит нашему предположению о том, что a и b не имеют общих делителей.

Таким образом, мы доказали, что √2 не может быть представлено в виде простой дроби и является иррациональным числом.

Аналогично можно доказать иррациональность других чисел, например, √3 или π. Эти доказательства требуют большего математического аппарата, однако их базовая идея остается та же: предположить, что число является рациональным, и показать, что это противоречит логике и свойствам чисел.

Свойства иррациональных чисел

Одно из удивительных свойств иррациональных чисел состоит в том, что они являются бесконечными и не повторяющимися. Например, число π (пи) — одно из самых известных иррациональных чисел и оно имеет десятичное представление, которое продолжается до бесконечности: 3.1415926535897932 и так далее, без какого-либо повторения групп цифр.

Другим свойством иррациональных чисел является то, что они не могут быть точно представлены в виде конечной десятичной дроби. Например, число √2 (квадратный корень из 2) не может быть записано в виде десятичной дроби с конечным количеством цифр после запятой, потому что оно бесконечное и не повторяющееся. Только в виде символа √2 мы можем представить его точно.

Иррациональные числа также обладают свойством неограниченности в рациональном числовом представлении. Например, число e (основание натурального логарифма) примерно равно 2.71828 и так далее, и его десятичное представление продолжается бесконечно без какого-либо закрытого встроенного шаблона.

Вот лишь несколько примеров свойств иррациональных чисел. Они удивительны и таинственны, и их изучение приносит много интереса и возможностей для исследования в математике.

Иррациональные числа и их применение в математике

Давай я расскажу тебе о нескольких примерах иррациональных чисел и их приложениях. Например, число π (пи) – это иррациональное число, изображающее отношение длины окружности к ее диаметру. Это число используется в геометрии и физике для расчетов окружностей и сфер.

Еще один пример – число √2 (корень из 2). Оно является иррациональным и используется в геометрии и алгебре для решения задач, связанных с прямоугольными треугольниками.

Можешь ли ты представить себе, что иррациональные числа встречаются и в таких ежедневных вещах, как музыка? Некоторые музыкальные ноты могут быть представлены иррациональными числами, и это помогает создавать гармоничную музыку.

Замечательно, как математика проникает в различные сферы нашей жизни, не так ли? Она помогает нам решать задачи, строить логические цепочки и находить красоту в мире. Иррациональные числа – это всего лишь один из множества примеров того, как математика может быть полезна и в то же время интригующей.

Итак, будешь ли ты исследовать мир иррациональных чисел и их применение в математике? Может быть, ты откроешь что-то новое и интересное в этой азбуке чисел!

Приближение иррациональных чисел

В данной статье мы рассмотрели понятие иррациональных чисел, которые не могут быть выражены дробью двух целых чисел. Они представляют собой бесконечные десятичные дроби без периода, такие как корень из двух или число пи.

Однако, из-за своей бесконечности, иррациональные числа невозможно представить точно в виде конечного числа символов. Поэтому мы используем приближения иррациональных чисел, чтобы работать с ними в математических вычислениях. Чем больше разрядность приближения, тем точнее результат.

Часто для приближения иррациональных чисел используют десятичные дроби, обрезая их до определенного количества знаков после запятой. Например, число пи можно представить приближенно как 3.14159. Чем больше знаков после запятой мы возьмем, тем точнее будет приближение к истинному значению числа.

Еще один способ приближения иррациональных чисел — использование дробей, таких как разложение числа в непрерывную дробь. Например, корень из двух можно представить как 1 + 1/(2 + 1/(2 + 1/(2 + …))). Чем больше элементов мы возьмем в этой непрерывной дроби, тем точнее будет приближение иррационального числа.

Важно понимать, что хотя приближения иррациональных чисел не дают нам точного значения, они позволяют нам работать с этими числами в математических вычислениях и решать разнообразные задачи. Приближение иррациональных чисел является неотъемлемой частью математики и широко используется в науке, инженерии и других областях.