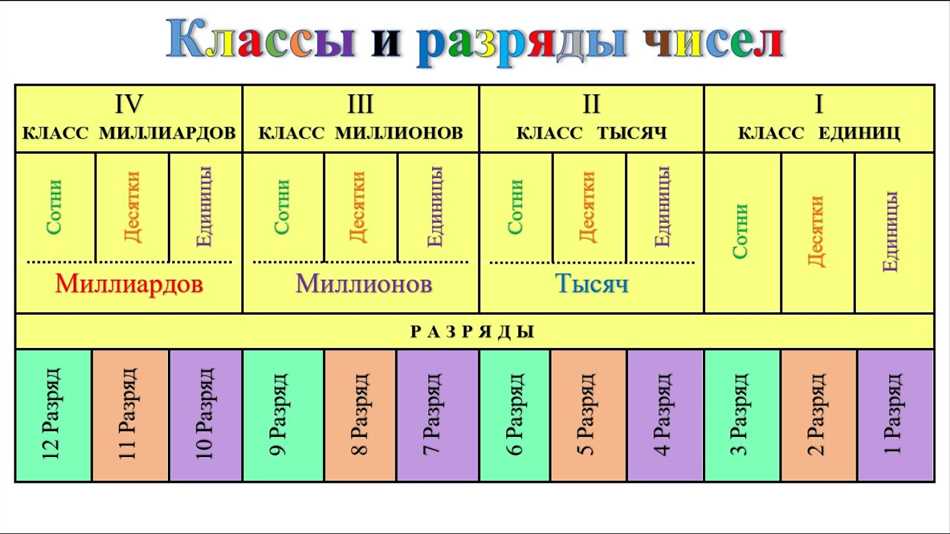
Когда мы говорим о числах в математике, мы можем классифицировать их по разрядам и классам. Разряды чисел указывают на позицию цифры в числе, в зависимости от ее значения. Например, в числе 54321, 5 находится в разряде тысяч, 4 — в разряде сотен, и так далее.
С другой стороны, классы чисел группируют числа в соответствии с их значением. Например, класс единиц включает в себя все однозначные числа (от 0 до 9), класс десятков — числа от 10 до 99, и так далее.
Понимание классов и разрядов чисел в математике помогает нам лучше понять структуру числовых систем и их свойства. Это основа для выполнения операций с числами, а также решения задач и создания математических моделей в различных областях науки и техники.
Необходимость классификации чисел
В мире математики существует огромное множество чисел, и чтобы немного разобраться в этом разнообразии, мы вводим понятие классификации чисел. Зачем нам это нужно? Давайте разберемся!
Классификация чисел помогает нам систематизировать и организовать числа по различным характеристикам. Это упрощает работу с числами и позволяет нам лучше понять их свойства и взаимосвязи.
Например, классификация чисел в разряды (натуральные числа, целые числа, рациональные числа и так далее) помогает нам понять, какие операции мы можем выполнять с этими числами и какие результаты получим. Это дает нам возможность строить более сложные математические модели и решать разнообразные задачи.
Классификация чисел также позволяет нам определить, какие числа имеют особые свойства. Например, если мы знаем, что число является простым, то мы можем использовать это свойство для решения различных задач и проблем.
Классификация чисел помогает нам также в повседневной жизни. Например, при покупке товаров в магазине мы используем целые числа для подсчета количества товаров и рациональные числа для вычисления стоимости.
Таким образом, классификация чисел является неотъемлемой частью математики и помогает нам лучше понимать и использовать числа в различных ситуациях. Без нее мы бы были ограничены и не смогли бы полностью раскрыть потенциал чисел.
Классы чисел
Ты когда-нибудь задавался вопросом, что такое классы чисел? Это довольно интересная и важная тема в математике, которая помогает нам организовать числа в разные группы в зависимости от их свойств и характеристик.
Возможно, ты уже слышал о разных классах чисел, таких как натуральные числа, целые числа, рациональные числа, иррациональные числа и действительные числа. Каждый из этих классов имеет свои особенности и связи с другими классами.
Натуральные числа — это числа, которые мы используем для счета предметов в реальном мире, такие как 1, 2, 3 и так далее. Целые числа включают натуральные числа и их отрицательные значения, такие как -1, -2, -3 и так далее.
Рациональные числа — это числа, которые могут быть представлены в виде дробей, где числитель и знаменатель являются целыми числами. Например, 1/2, -3/4 и 7/5 — все они являются рациональными числами.
Иррациональные числа, в свою очередь, не могут быть представлены в виде обыкновенной дроби. Например, числа пи (π) и корень квадратный из 2 (√2) являются иррациональными числами.
И, наконец, действительные числа включают в себя как рациональные, так и иррациональные числа.
Вот так! Теперь у тебя есть понимание о том, что такое классы чисел и как они связаны друг с другом. Это может показаться сложным на первый взгляд, но на самом деле это очень полезное знание для понимания основ математики. Используй его, чтобы разобраться в различных математических проблемах и задачах, которые встретятся тебе в будущем!
Натуральные числа
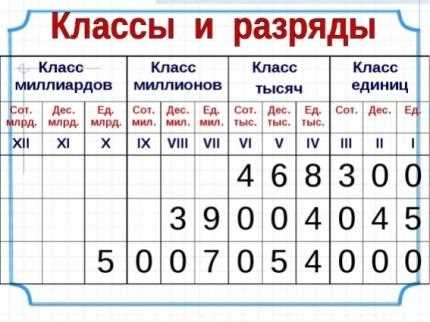
Мы используем натуральные числа каждый день без особого внимания. Когда перечисляем предметы, например, яблоки или книги, мы используем натуральные числа, чтобы определить, сколько их. Натуральные числа также используются, чтобы указывать возраст, например, сколько лет тебе или твоим друзьям.
Натуральные числа выглядят просто, но они имеют свои свойства и характеристики. Они образуют бесконечную последовательность, начиная с числа 1 и увеличиваясь на 1 каждый раз. Например: 1, 2, 3, 4, 5, и так далее. Мы можем складывать, вычитать, умножать и делить натуральные числа, чтобы получить новые числа и решить разные задачи.
Натуральные числа также могут быть классифицированы по разрядам, как однозначные, двузначные, трехзначные и т.д. Это позволяет нам организовывать числа в группы и работать с ними более удобно.
Так что следующий раз, когда ты считаешь яблоки в своей корзине или делишься своим возрастом, помни, что ты используешь натуральные числа, чтобы делать это. И помни, что каждое число имеет свою особенность и значение в нашей жизни.
Целые числа
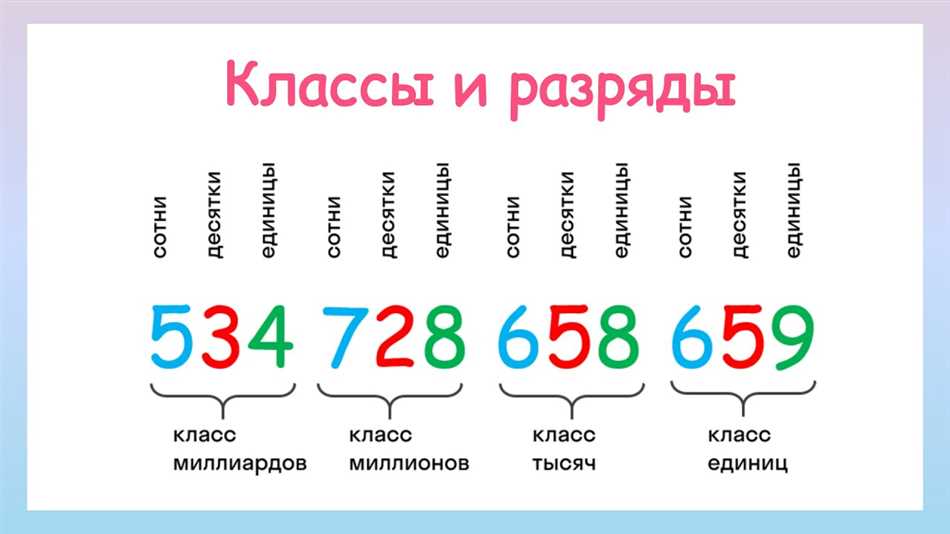
Целые числа можно представить на числовой прямой, где положительные числа находятся справа от нуля, а отрицательные числа — слева. Ноль находится в центре прямой.
Целые числа могут использоваться для описания реальных ситуаций или объектов. Например, количество денег на банковском счете, температура воздуха или количество учеников в классе — все это можно выразить целым числом.
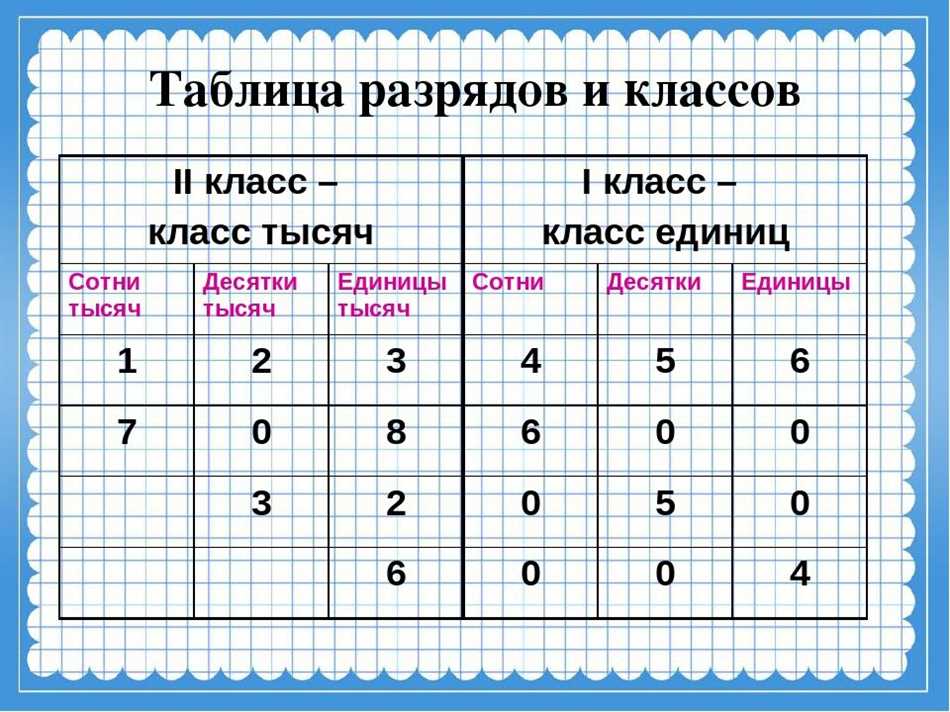
Целые числа могут быть определены в различных классах, в зависимости от их размера. Например, есть классы целых чисел, таких как единицы, десятки, сотни и так далее. Каждый класс имеет свое значение и разрядность — чем выше разрядность, тем больше значение числа.
Целые числа очень важны в математике и имеют широкое применение во многих областях науки и технологий. Например, они используются в алгоритмах и программировании для работы с данными и выполнения различных вычислений.
Заключение
Важно отметить, что рациональные числа обладают такими свойствами, как закон сокращения и сложение/вычитание/умножение/деление. Они используются не только в математике, но и в других областях, таких как физика и экономика, для представления и сравнения количественных данных и величин.
Изучение рациональных чисел позволяет нам лучше понять и использовать числа в повседневной жизни. Они помогают нам работать с дробями и проводить различные операции с числами, что актуально как в нашей повседневной жизни, так и в профессиональных сферах деятельности.
Вопрос-ответ:
Что такое рациональные числа?
Рациональные числа — это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами.
Какие числа являются рациональными?
К рациональным числам относятся все целые числа, десятичные дроби, обыкновенные дроби и корни из положительных целых чисел.
Как проверить, является ли число рациональным?
Чтобы проверить, является ли число рациональным, необходимо представить его в виде дроби a/b, где a и b — целые числа. Если удается найти такие значения a и b, то число является рациональным, в противном случае — иррациональным.