Коэффициент асимметрии – это статистическая мера, которая позволяет оценить асимметрию распределения данных. Он показывает, насколько распределение данных отличается от симметричного.
Формула коэффициента асимметрии рассчитывается следующим образом: коэффициент асимметрии = (среднее значение – мода) / стандартное отклонение. Если коэффициент асимметрии равен 0, то распределение считается симметричным. Если коэффициент больше 0, то распределение смещено вправо, а если меньше 0 – влево.
Интерпретация коэффициента асимметрии заключается в оценке формы распределения данных. Она помогает понять, есть ли асимметрия, и в какую сторону она проявляется. Зная эту информацию, можно принимать более обоснованные решения на основе статистического анализа данных.
- Определение коэффициента асимметрии
- Что такое коэффициент асимметрии?
- Зачем нужен коэффициент асимметрии?
- Формула коэффициента асимметрии
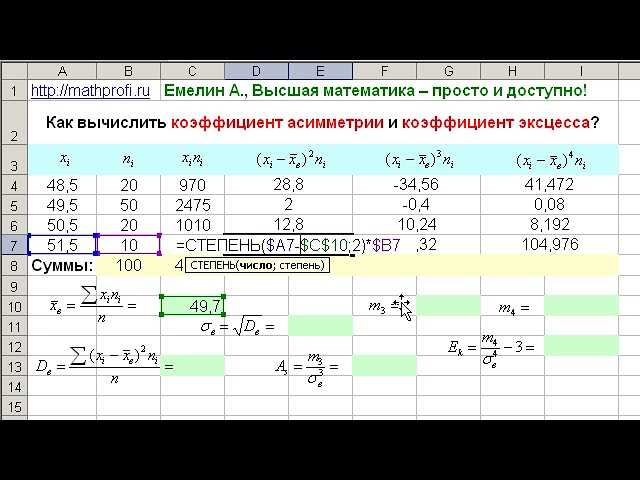
- Как вычислить коэффициент асимметрии?
- Как интерпретировать значение коэффициента асимметрии?
- Вопрос-ответ:
- Как интерпретировать значение коэффициента асимметрии, равное 0?
- Как интерпретировать значение коэффициента асимметрии, большее нуля?
- Как интерпретировать значение коэффициента асимметрии, меньшее нуля?
Определение коэффициента асимметрии

В простых словах, коэффициент асимметрии позволяет узнать, есть ли в выборке больше значений, сконцентрированных вокруг среднего, или же имеется выбросы, которые вызывают смещение. Его значение может быть положительным, отрицательным или равным нулю. Если коэффициент асимметрии равен нулю, это означает, что распределение симметрично относительно средней точки. Если значение положительное, то распределение смещено вправо, а если отрицательное, то влево.
Коэффициент асимметрии может быть полезным в различных областях, таких как финансы, экономика, биология и другие. Например, его можно использовать для анализа доходности акций, изучения роста популяции или исследования распределения генетических данных.
Что такое коэффициент асимметрии?
Для вычисления коэффициента асимметрии используется формула, которая учитывает отклонение данных от среднего значения и их вариацию. Положительное значение коэффициента асимметрии указывает на правостороннюю асимметрию, то есть наличие длинного хвоста справа от среднего значения. Это означает, что данные имеют больше значений, превышающих среднее, чем тех, которые меньше него.
- С пример положительного коэффициента асимметрии можно связать с процентами и оценками: в большинстве случаев, они распределены с правосторонней асимметрией, так как часто бывает много людей с высокими результатами.
С другой стороны, отрицательное значение коэффициента асимметрии указывает на левостороннюю асимметрию, то есть присутствие длинного хвоста слева от среднего значения. Это говорит о том, что данные имеют больше значений, меньших среднего, чем тех, которые его превышают.
- Пример отрицательного коэффициента асимметрии может быть связан с расходами домашних хозяйств: обычно они имеют левостороннюю асимметрию, потому что некоторые домашние хозяйства имеют очень высокий уровень расходов, тогда как большинство — ниже среднего.
Зачем нужен коэффициент асимметрии?
Вы когда-нибудь задумывались, почему люди интересуются коэффициентом асимметрии и зачем он им нужен? Давайте разберемся.
Коэффициент асимметрии — это статистическая мера, которая позволяет измерить симметрию распределения значений величины. Он показывает, насколько среднее значение отличается от медианы и может помочь понять, насколько асимметричны данные.
Зачем нам эта информация? Ну, представьте, что у вас есть выборка данных о доходах людей в определенном городе. По графику распределения доходов вы можете увидеть, что большинство людей имеют доход, близкий к среднему значению. Однако, если коэффициент асимметрии положителен, это означает, что существует небольшая группа людей, которые имеют очень высокий доход и значительно смещают среднее значение.
А что если у вас есть данные о акциях? Вы можете использовать коэффициент асимметрии, чтобы определить, насколько равномерно распределен доход от акций. Если коэффициент отрицателен, это может указывать на то, что больше акций имеют низкую доходность, а меньше — высокую.
И так, для кого-то коэффициент асимметрии — просто статистический инструмент. Но для аналитиков данных он может быть ценным инструментом для понимания различных распределений и их особенностей. Вы не настолько увлекаетесь статистикой, чтобы использовать коэффициент асимметрии каждый день, но по крайней мере, вы знаете, что это и для чего он нужен.
Формула коэффициента асимметрии
В общем случае, формула коэффициента асимметрии выглядит следующим образом:
Асимметрия = 3 * (Среднее значение — Мода) / Стандартное отклонение
В этой формуле участвуют три показателя: среднее значение, мода и стандартное отклонение.
Среднее значение — это сумма всех значений, деленная на их количество. Мода — это значение, которое встречается наиболее часто в наборе данных. Стандартное отклонение — это мера разброса данных относительно их среднего значения.
После подсчета этих показателей и их вставки в формулу, получается число, которое интерпретируется следующим образом: если коэффициент асимметрии положителен, это означает, что данные имеют правостороннюю асимметрию (тяжелый хвост справа), если коэффициент асимметрии отрицателен, то данные имеют левостороннюю асимметрию (тяжелый хвост слева). Если значение равно нулю, это говорит о симметричности данных.
Как вычислить коэффициент асимметрии?
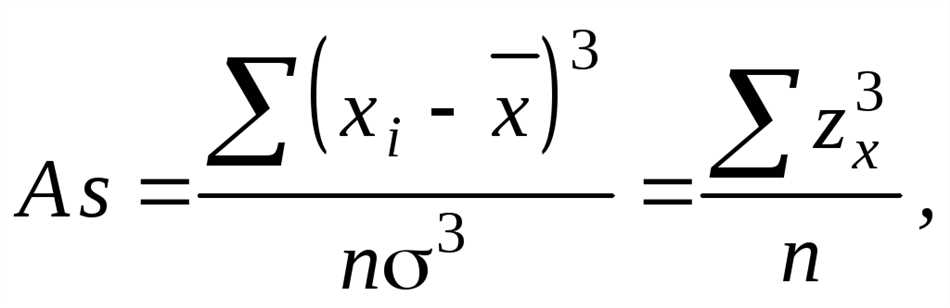
Чтобы вычислить коэффициент асимметрии, нам нужно знать значения всех наблюдений в выборке. Сначала мы вычисляем среднее значение и стандартное отклонение выборки. Затем мы используем эти значения в формуле для коэффициента асимметрии.
Формула для коэффициента асимметрии выглядит следующим образом:
Асимметрия = (3 * (среднее значение — медиана)) / стандартное отклонение
Получившийся результат может быть положительным или отрицательным. Если коэффициент асимметрии больше нуля, значит, мы имеем дело с положительной асимметрией, то есть распределение смещено вправо. Если коэффициент асимметрии меньше нуля, то распределение смещено влево и называется отрицательной асимметрией. Если коэффициент асимметрии равен нулю, это означает, что распределение симметрично.
Формула может показаться сложной для понимания, но не беспокойся! Можно использовать различные программы и инструменты для автоматического вычисления коэффициента асимметрии. Это существенно упростит тебе задачу.
Как интерпретировать значение коэффициента асимметрии?
Интерпретация значения коэффициента асимметрии зависит от его знака и абсолютной величины:
- Если коэффициент асимметрии равен нулю, это означает, что распределение данных является симметричным. Левый и правый хвосты распределения равны, и нет явно выраженного перекоса.
- Если коэффициент асимметрии положителен, это указывает на преобладание длинного правого хвоста. Данные имеют тенденцию к смещению вправо и имеют более выраженный «хвост» в этом направлении.
- Если коэффициент асимметрии отрицателен, это указывает на преобладание длинного левого хвоста. Данные имеют тенденцию к смещению влево и имеют более выраженный «хвост» в этом направлении.
Интерпретация абсолютной величины коэффициента асимметрии может быть связана с его значимостью:
- Если абсолютное значение коэффициента асимметрии меньше 1, то различия в асимметрии считаются незначительными и данные можно считать примерно симметричными.
- Если абсолютное значение коэффициента асимметрии между 1 и 2, то различия в асимметрии считаются умеренными и данные имеют умеренную асимметрию.
- Если абсолютное значение коэффициента асимметрии больше 2, то различия в асимметрии считаются значительными и данные имеют значительную асимметрию.
Интерпретация значения коэффициента асимметрии позволяет получить информацию о форме распределения данных и понять, насколько они отклоняются от симметрии. Этот показатель полезен при анализе данных и может помочь исследователю лучше понять изучаемые явления.
Вопрос-ответ:
Как интерпретировать значение коэффициента асимметрии, равное 0?
Значение коэффициента асимметрии, равное 0, означает, что распределение данных симметрично. Это означает, что данные имеют одинаковые вероятности находиться как влево, так и вправо от среднего значения. В данном случае, среднее значение равно медиане, и данные распределены равномерно вокруг этого значения.
Как интерпретировать значение коэффициента асимметрии, большее нуля?
Значение коэффициента асимметрии, большее нуля, означает положительную асимметрию или смещение вправо. Это означает, что распределение данных имеет более высокие значения справа от среднего значения. В этом случае, медиана будет меньше среднего значения, и большинство данных сосредоточено слева от среднего.
Как интерпретировать значение коэффициента асимметрии, меньшее нуля?
Значение коэффициента асимметрии, меньшее нуля, означает отрицательную асимметрию или смещение влево. Это означает, что распределение данных имеет более высокие значения слева от среднего значения. В этом случае, медиана будет больше среднего значения, и большинство данных сосредоточено справа от среднего.




