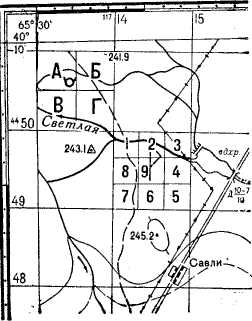
Когда мы слышим слово «координаты», нам сразу на ум приходит мысль о картах или глобусах. И действительно, координатная сетка является основой для представления точек на плоскости или на поверхности. Это система взаимосвязанных пересечений вертикальных и горизонтальных линий, которые образуют клетки. Каждая точка на сетке имеет свои уникальные числовые значения, которые называются координатами.
Основная цель координатной сетки — помочь нам определить конкретное положение объекта или местоположение на карте. Благодаря координатам, мы можем точно указать, где находится объект и как далеко он находится от других точек. Координатная сетка широко используется в географии, навигации, математике, компьютерной графике и других областях, где точность и позиционирование важны.
- Раздел 1: Основные принципы координатной сетки
- Подраздел 1.1: Определение координатной сетки
- Подраздел 1.2: Структура координатной сетки
- Раздел 2: Координатная сетка на плоскости
- Подраздел 2.1: Декартова система координат
- Подраздел 2.2: Полярная система координат
- Вопрос-ответ:
- Какие основные принципы лежат в основе полярной системы координат?
- Как можно перевести координаты из декартовой системы в полярную и наоборот?
- В каких областях применяется полярная система координат?
Раздел 1: Основные принципы координатной сетки
Чтобы понять, как работает координатная сетка, представьте себе шахматную доску. У каждой клетки на доске есть свои координаты: буквенные и числовые. Например, клетка А1 имеет координаты А (вертикальная ось) и 1 (горизонтальная ось).
Координатные сетки используются во многих областях, таких как картография, инженерия, графика, физика и многих других. Координатная сетка позволяет точно определить местоположение объектов и решать различные задачи.
Для работы с координатной сеткой необходимо знать основные принципы и обозначения. Горизонтальные линии обычно называются осью абсцисс, а вертикальные линии — осью ординат. Координаты обозначаются в виде пары чисел (x, y), где x — это значение на оси абсцисс, а y — значение на оси ординат.
Теперь, когда мы разобрались в основных принципах координатной сетки, давайте перейдем к рассмотрению ее применения в различных областях. Мы будем исследовать, как координатная сетка помогает нам навигировать по миру и решать сложные задачи. В следующем разделе мы рассмотрим применение координатной сетки в картографии.
Подраздел 1.1: Определение координатной сетки
Каждая точка в координатной сетке имеет уникальную пару координат (X, Y), где X – значение по горизонтальной оси, а Y – значение по вертикальной оси. Например, точка (2,4) находится 2 единицы вправо от начала координат и 4 единицы вверх от него. Такой способ обозначения точек позволяет определить местоположение объекта с высокой точностью и использовать координатную сетку в различных областях, таких как графики, картография, программирование и другие.
Определение координатной сетки может быть полезно при решении задач в геометрии, физике или при построении графиков функций. Знание основных принципов координатной сетки позволяет легко манипулировать точками и объектами на плоскости и представлять их графически. Так что, если вы когда-либо сталкиваетесь с непонятными картами, графиками или расположением объектов на плоскости, помните, что координатная сетка поможет вам разобраться и найти нужное местоположение или ответ на ваш вопрос.
Подраздел 1.2: Структура координатной сетки
Каждая точка на плоскости имеет свои координаты, которые определяются по горизонтальной и вертикальной оси. Например, точка с координатами (3, 2) находится на 3 единицы вправо от начала координат по X-оси и на 2 единицы вверх от начала координат по Y-оси.
Структура координатной сетки позволяет нам легко определить расстояние между точками и установить взаимное положение объектов. Например, если мы хотим найти расстояние между двумя точками на плоскости, мы можем использовать теорему Пифагора или просто вычислить разницу между их координатами по X- и Y-оси.
Координатная сетка имеет широкое применение в различных областях, таких как математика, физика, графика и картография. Она помогает нам легко представлять и анализировать данные, строить графики функций, определять направление и расстояние в пространстве.
Раздел 2: Координатная сетка на плоскости
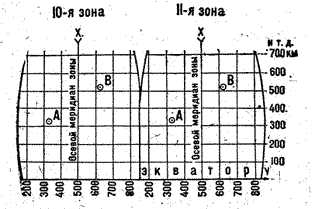
Вы наверняка видели графики на осях, где по горизонтальной оси отображается значение переменной X, а по вертикальной оси — значение переменной Y. В этом случае каждая точка на графике имеет свои координаты (X, Y).
Но как мы можем определить эти координаты? Для этого мы используем координатную сетку. Координатная сетка состоит из горизонтальных и вертикальных линий, которые пересекаются в определенных точках. Каждая точка на сетке имеет свои уникальные координаты. Например, точка A может иметь координаты (2, 5), а точка B — координаты (-3, 1).
Чтобы найти координаты точки на координатной сетке, мы смотрим, на какую линию пересекается вертикальная и горизонтальная линии, и затем читаем числа на осях. Например, если мы ищем координаты точки, которая находится на правой стороне от 0 по оси X и выше 0 по оси Y, то это будут положительные числа.
Координатная сетка широко используется в математике, физике, геометрии, а также в инженерии и в науке о данных. Она позволяет нам точно определить положение объекта или точки на плоскости и помогает нам решать различные задачи и вычисления. Важно освоить понятие координатной сетки, чтобы быть готовыми к решению математических и научных задач.
Подраздел 2.1: Декартова система координат
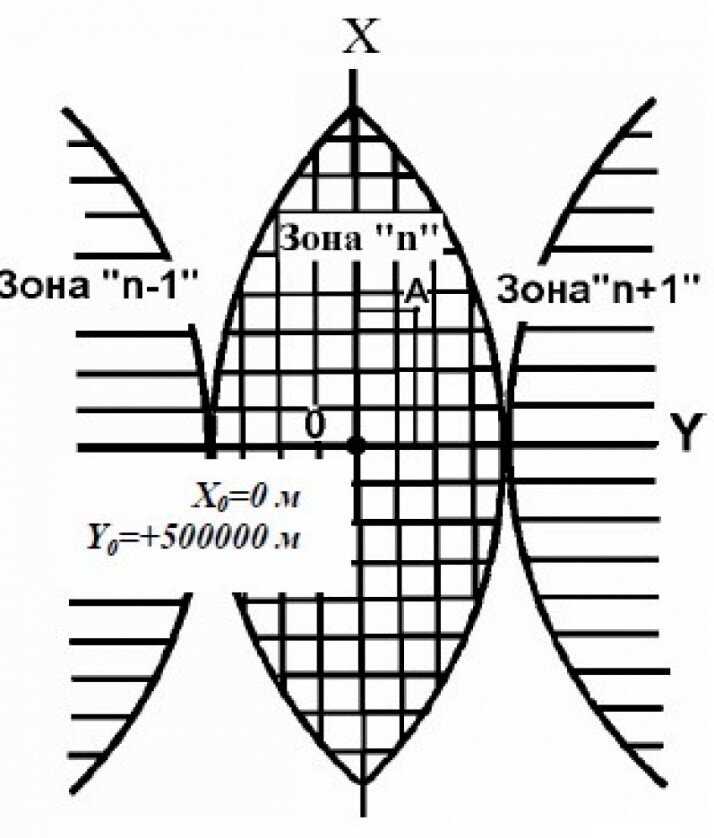
Чтобы понять, как работает декартова система координат, представь себе плоскость, на которой нарисованы две перпендикулярные прямые линии. Одна из них называется осью x, а другая — осью y. В точке пересечения этих линий находится начало координат, обозначаемое точкой (0,0).
Координаты точки определяются расстоянием от нее до осей x и y. На оси x положительные значения находятся направо от начала координат, а отрицательные значения — налево. На оси y положительные значения находятся вверх от начала координат, а отрицательные — вниз.
Теперь давай представим, что ты хочешь описать положение точки A на плоскости с помощью координат. Если точка A находится 3 единицы вправо от начала координат и 4 единицы вверх от него, ты можешь записать ее координаты как (3,4). Просто подсчитываешь расстояние до осей x и y, и записываешь значения в скобках, разделяя их запятой.
Декартова система координат используется в различных областях, включая математику, физику, графику и даже навигацию. Она позволяет точно определить положение объекта на плоскости и с легкостью проводить различные вычисления и анализы.
Подраздел 2.2: Полярная система координат
Итак, мы уже узнали много интересного о декартовой системе координат, которая основана на осях x и y. Но есть и другая система координат, называемая полярной. Как ты думаешь, в чем заключается ее отличие?
В полярной системе координат мы используем угол и расстояние от начала координат (полюса) до точки для определения ее положения. Представь, что ты стоишь в центре поля и тебя окружают деревья. Угол указывает, в каком направлении ты смотришь, а расстояние — насколько далеко ты находишься от каждого дерева.
Например, можешь представить полярную систему координат как большой круг, где полюс находится в центре. Линия, исходящая из полюса, представляет собой радиус, а угол от положительной оси x задает направление. Таким образом, точка может быть определена своим радиусом и углом.
Полярная система координат находит свое применение в различных областях, таких как физика, математика и инженерия. Например, она используется для описания движения объектов, анализа колебаний и определения полярности электрических зарядов.
Так что декартова система координат и полярная система координат предлагают различные способы описания и измерения положения точек в пространстве. Теперь ты знаешь, как использовать полярную систему координат и зачем она нужна!
Вопрос-ответ:
Какие основные принципы лежат в основе полярной системы координат?
Полярная система координат использует две величины, радиус и угол, чтобы определить положение точки в двумерном пространстве. Радиус указывает на расстояние от начала координат до точки, а угол указывает на направление точки от начала координат.
Как можно перевести координаты из декартовой системы в полярную и наоборот?
Для перевода из декартовой системы координат в полярную нужно использовать формулы r = √(x^2 + y^2) и θ = arctan(y/x). Для перевода из полярной системы в декартову используются формулы x = r*cos(θ) и y = r*sin(θ).
В каких областях применяется полярная система координат?
Полярная система координат широко применяется в физике, математике и инженерии для описания и решения задач, связанных с циклическими и симметричными структурами. Она также часто используется для описания полярных координат объектов в природе, таких как орлы и полюса магнитных полей.