Что такое корреляция в статистике простыми словами?

Корреляция – это показатель, который помогает нам понять, насколько две величины взаимосвязаны. Другими словами, мы можем использовать корреляцию, чтобы узнать, насколько два явления изменяются вместе. Если одно явление увеличивается, а другое тоже увеличивается, то между ними есть позитивная корреляция. Например, чем больше времени мы проводим занимаясь спортом, тем больше калорий мы сжигаем. Если же одно явление увеличивается, а другое уменьшается, то между ними есть негативная корреляция. Например, чем больше питаемся мороженым, тем меньше нам нравится холод в комнате. Корреляция может быть положительной, отрицательной или отсутствовать вовсе.

Корреляция и ее значения

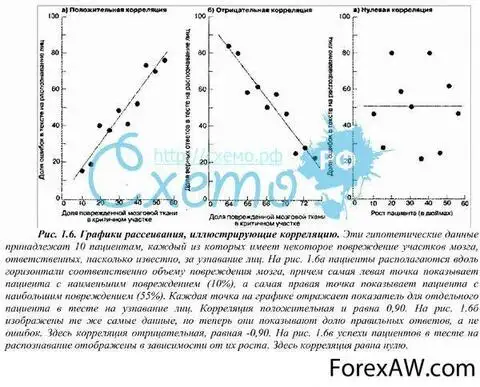
Когда мы говорим о корреляции в статистике, мы обычно имеем в виду связь между двумя или более наборами данных. Корреляция может быть положительной, отрицательной или нулевой, и каждая из этих вариантов имеет своё значение.

Положительная корреляция означает, что чем выше значение одного набора данных, тем выше значение другого набора данных. Например, положительная корреляция может быть между температурой и количеством продаж мороженого — чем выше температура, тем больше мороженого покупают.

С другой стороны, отрицательная корреляция означает, что чем выше значение одного набора данных, тем ниже значение другого набора данных. Например, отрицательная корреляция может быть между количеством часов, проведенных на тренировках, и уровнем стресса — чем больше времени тратится на тренировки, тем меньше стресса.

Нулевая корреляция, как можно догадаться, означает отсутствие связи между наборами данных. Это может быть, например, в случае, когда анализируются случайные или независимые наборы данных.

Понимание корреляции помогает нам понять, как одни переменные влияют на другие, и может помочь принимать более осознанные решения на основе данных. А ты знал о значении корреляции?

Примеры корреляции

Давай рассмотрим несколько примеров корреляции, чтобы лучше понять, как она работает.

• Корреляция между количеством употребления кофе и уровнем энергии: Если ты заметил, что когда ты пьешь больше кофе, ты чувствуешь себя более энергичным, то между этими двумя переменными может существовать положительная корреляция.

• Корреляция между температурой воздуха и продажами мороженого: Обычно в летние месяцы, когда температура воздуха повышается, продажи мороженого также возрастают. Это может указывать на положительную корреляцию между этими двумя переменными.

• Корреляция между количеством выпавших осадков и урожаем сельскохозяйственных культур: Если в местности выпадает больше осадков, обычно урожай становится более обильным. Таким образом, здесь существует положительная корреляция между количеством осадков и урожаем.

Это всего лишь несколько примеров корреляции, которые мы можем обнаружить в повседневной жизни. Интересно заметить, как переменные взаимодействуют друг с другом и как одна переменная может быть связана с другой.

Статистическая мера корреляции

Ты знаешь, что такое корреляция? Это статистическая мера, которая показывает, насколько две переменные связаны между собой. А что это значит? Представь себе, что у тебя есть два признака, например, твой возраст и твоя зарплата. И ты задаешься вопросом, есть ли связь между этими двумя переменными.

Статистическая мера корреляции, такая как коэффициент корреляции Пирсона, может помочь ответить на этот вопрос. Она дает числовую оценку связи между переменными, которая варьируется от -1 до 1. Если коэффициент равен 1, это значит, что есть положительная связь между переменными: чем больше возраст, тем выше зарплата.

Если коэффициент равен -1, это означает, что есть отрицательная связь: чем старше человек, тем ниже его зарплата. И если коэффициент равен 0, значит, нет связи между переменными.

Таким образом, статистическая мера корреляции помогает нам понять, как одна переменная зависит от другой. Это очень полезный инструмент для исследования различных явлений в нашей жизни. Так что, следующий раз, когда у тебя возникнет вопрос о связи между переменными, не забудь вспомнить про корреляцию!

Когда и зачем используется корреляция?

Корреляция используется в различных областях, таких как экономика, социология, биология и многих других. Она помогает ученым и исследователям выявить тесноту связи между различными переменными и определить, насколько эти переменные влияют друг на друга.

Корреляция может использоваться для:

• Оценки взаимосвязи между двумя переменными;
• Предсказания значений одной переменной на основе другой;
• Изучения влияния различных факторов на определенное явление;
• Выявления причинно-следственных связей;
• Идентификации аномалий или выбросов в данных.

Все эти задачи могут быть полезны для принятия обоснованных решений в различных областях деятельности. Например, в экономике корреляция может использоваться для определения взаимосвязи между доходом и расходами, что помогает принять решение о целесообразности определенных инвестиций. В медицине корреляция может использоваться для определения связи между заболеваниями и факторами риска, что помогает разработать эффективные стратегии профилактики и лечения.

В целом, корреляция – это мощный инструмент анализа данных, который позволяет выявлять взаимосвязи и делать предсказания. Он способствует более глубокому пониманию и изучению различных явлений и помогает принимать обоснованные решения на основе полученных результатов.