Что такое кратное число в математике: основные понятия и примеры

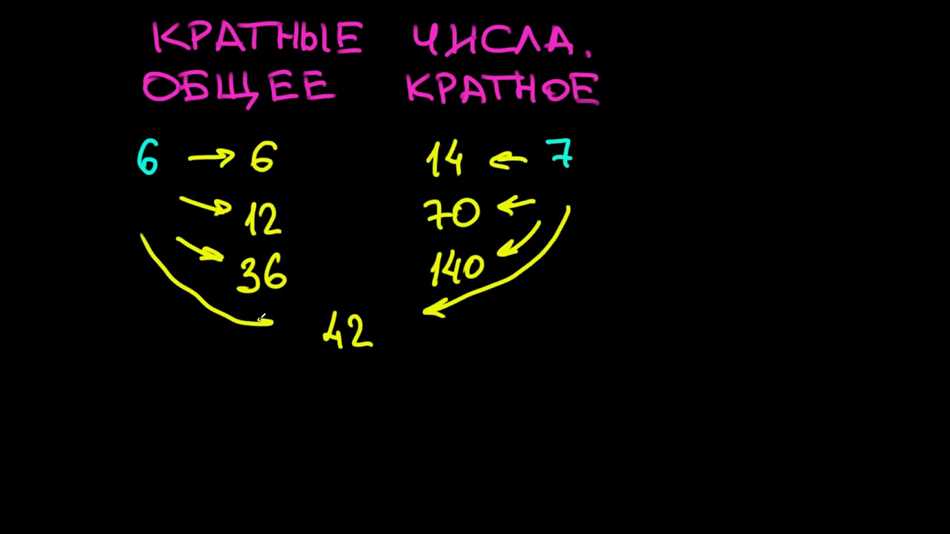
Когда мы говорим о кратных числах в математике, мы имеем в виду числа, которые делятся на другое число без остатка. Другими словами, если одно число является кратным другого, то оно может быть разделено на это число без остатка.

Например, если мы говорим о числе 12, то оно кратно числам 1, 2, 3, 4, 6 и 12, потому что оно делится на эти числа без остатка. Иначе говоря, 12 является кратным 1, 2, 3, 4, 6 и 12.

Кратные числа имеют важное значение в математике и используются в разных областях, например, в делении, пропорциях и дробях. Понимание кратных чисел поможет нам решать сложные задачи и строить логические цепочки аргументации.

Определение кратного числа

Наверняка каждому из нас приходилось слышать или видеть термин «кратное число», но что же это означает? Давайте посмотрим.

Кратное число — это число, которое делится на другое число без остатка. Другими словами, когда мы делим одно число на другое, если результат деления является целым числом, то первое число является кратным второму.

Например, давайте рассмотрим число 12. Оно является кратным числам 2, 3 и 4, потому что 12 делится на эти числа без остатка. Однако, 12 не является кратным числу 5, потому что 12 делится на 5 с остатком.

Таким образом, чтобы определить, является ли число кратным другому, нужно поделить первое число на второе и проверить, получается ли целое число или остаток. Если результат деления — целое число, то первое число является кратным второму.

Теперь, когда мы знаем, что такое кратное число, давайте посмотрим, как мы можем использовать это в математике и повседневной жизни. Ответ прост — кратные числа могут использоваться для решения различных задач и проблем.

• В математике кратные числа широко используются в делении, нахождении общего кратного, и в других арифметических операциях.
• В нашей повседневной жизни кратные числа могут помочь нам решать проблемы с расписанием (например, когда автобусы отправляются каждые 15 минут), планировать повторяющиеся события (например, удобно планировать еженедельные встречи в одно и то же время) или даже делать простые математические вычисления (например, вычислять стоимость товаров при определенных скидках).

Итак, вот оно, определение кратного числа. Теперь вы знаете, что такое кратное число и как оно может быть полезно в математике и повседневной жизни. Надеюсь, что этот беглый обзор помог вам лучше понять этот математический термин и его применение.

Как определить кратность числа

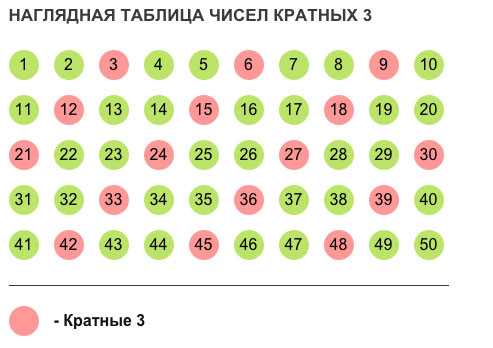
Чтобы определить, является ли число кратным другому числу, нужно проверить, делится ли одно на другое без остатка. Например, чтобы узнать, кратно ли число 6 числу 3, нужно разделить 6 на 3. Если результат деления будет целым числом, то значит, число 6 кратно числу 3.

Обычно, чтобы легче определить кратность числа, используются таблицы умножения. Если число делится на все числа, записанные в строке или столбце таблицы умножения, то оно является кратным.

Определение кратности числа нам помогает лучше понять свойства чисел и отношения между ними. Например, зная, что число кратно двум, мы понимаем, что оно является четным.

Кратность числа и деление

Чтобы понять, является ли одно число кратным другому, мы можем использовать деление. Возьмем два числа: делимое и делитель. Если делитель делит делимое без остатка, то делимое является кратным делителю.

Рассмотрим пример: 15 кратно 3, потому что 15 делится на 3 без остатка. Если мы разделим 15 на 3, получим 5 без остатка. Таким образом, 15 является кратным числу 3.

Кратность числа может быть полезной во многих ситуациях. Например, если вы хотите разделить некоторую сумму денег поровну между несколькими людьми, вам нужно знать, является ли общая сумма кратной количеству людей. Если нет, то нужно будет найти другой способ разделить деньги.

Деление и кратность также широко используются в алгебре и арифметике. Понимание этих понятий поможет вам в решении уравнений, нахождении общего кратного нескольких чисел и в других математических проблемах.

Так что, если вы когда-нибудь встретитеся с числами и задумаетесь о кратности, помните, что это просто способ описать, делится ли одно число на другое без остатка. Это важное понятие, которое поможет вам лучше понять математику и расширить свои знания в этой области.

Примеры кратных чисел

Теперь давайте рассмотрим несколько примеров:

• Число 4 кратно числу 2, так как 4 делится на 2 без остатка.
• Число 10 кратно числу 5, так как 10 делится на 5 без остатка.
• Число 15 кратно числу 3, так как 15 делится на 3 без остатка.

Видите ли вы, как просто? Теперь давайте попробуем найти еще несколько примеров самостоятельно:

• Найдите кратное число числа 6.
• Найдите кратное число числа 9.

Проверьте свои ответы:

• Кратным числом числа 6 является, например, число 12, так как 12 делится на 6 без остатка.
• Кратным числом числа 9, например, является число 27, так как 27 делится на 9 без остатка.

Надеюсь, теперь вы лучше понимаете, что такое кратные числа и как их найти. Продолжайте практиковаться и помните, что математика может быть увлекательной и полезной!

Свойства кратных чисел

Наверняка, ты уже слышал о кратных числах. Ты уверенно знаешь, что они делятся нацело на другое число, но знаешь ли ты все их свойства?

Первое свойство кратных чисел — они возрастают по мере увеличения делителя. Например, если число кратно 2, то оно также будет кратным и числу 4, 6, 8 и так далее. Представляешь, какая мощная последовательность чисел получается!

Еще одно интересное свойство — если число кратно какому-то числу, то оно кратно и всем его делителям. Например, если число кратно 4, то оно будет кратным и числам 2 и 1. Это чудесно!

И наконец, последнее свойство. Если два числа кратны одному и тому же числу, то их сумма и разность также будут кратны этому числу. Это просто волшебно, не так ли?

Итак, кратные числа — это наше тайное оружие в мире математики. Они представляют собой не только порядок и систему, но и красоту и гармонию чисел. Используй их с умом и раскрой все их мощные свойства!