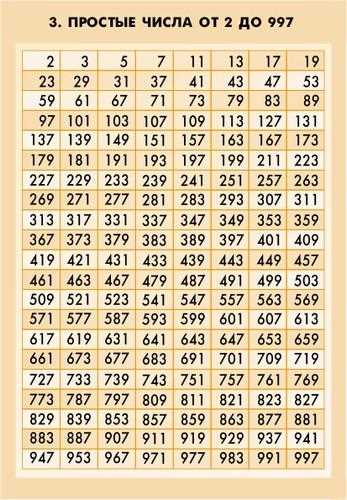
Решето Эратосфена — это метод поиска простых чисел, разработанный греческим математиком и астрономом Эратосфеном.
Решето Эратосфена основано на простом принципе: сначала создается список чисел от 2 до заданного числа N, а затем исключаются все составные числа, оставляя только простые числа. Как это происходит? Проходим по списку чисел, начиная с 2, и вычеркиваем все их кратные числа. Затем переходим к следующему не вычеркнутому числу и повторяем процесс. Продолжаем до тех пор, пока не закончатся числа в списке.
Решето Эратосфена является эффективным способом поиска простых чисел, особенно при работе с большими числами. Оно широко используется в различных областях, включая криптографию, математическую статистику и алгоритмы.
Основы решета Эратосфена
Таким образом продолжаем до тех пор, пока не достигнем конца списка. Все не отмеченные числа останутся простыми числами.
Например, представим, что у нас есть список чисел от 2 до 30:
- 2 (простое)
- 3 (простое)
- 4 (составное)
- 5 (простое)
- 6 (составное)
- 7 (простое)
- 8 (составное)
- 9 (составное)
- 10 (составное)
- 11 (простое)
- 12 (составное)
- 13 (простое)
- 14 (составное)
- 15 (составное)
- 16 (составное)
- 17 (простое)
- 18 (составное)
- 19 (простое)
- 20 (составное)
- 21 (составное)
- 22 (составное)
- 23 (простое)
- 24 (составное)
- 25 (составное)
- 26 (составное)
- 27 (составное)
- 28 (составное)
- 29 (простое)
- 30 (составное)
Итак, мы получаем список всех простых чисел от 2 до 30: 2, 3, 5, 7, 11, 13, 17, 19, 23 и 29.
Принцип решета Эратосфена

Итак, давай разберемся, как работает решето Эратосфена. Не волнуйся, это не сложно!
Возьмем некоторое число n, до которого мы хотим найти все простые числа. Создадим список всех чисел от 2 до n включительно. Для начала отметим, что число 2 является простым числом, поэтому оставим его в списке. Затем перейдем к числу 3 и вычеркнем все его кратные числа. После этого перейдем к следующему невычеркнутому числу и повторим этот процесс.
Давай посмотрим на пример, чтобы было проще понять. Предположим, что мы хотим найти все простые числа до 30. Создадим список чисел от 2 до 30 и начнем вычеркивать:
- Вычеркиваем все числа, кратные 2: 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30
- Переходим к следующему невычеркнутому числу — 3 и вычеркиваем его кратные числа: 6, 9, 12, 15, 18, 21, 24, 27, 30
- Переходим к следующему невычеркнутому числу — 5 и вычеркиваем его кратные числа: 10, 15, 20, 25, 30
- И так далее…
Когда останутся только невычеркнутые числа, это и будут все простые числа до заданного числа.
Получается, что решето Эратосфена является очень эффективным методом для вычисления простых чисел. Оно позволяет нам максимально быстро и просто находить все простые числа до заданного числа.
Так что, если тебе интересно мир математики и ты хочешь научиться находить простые числа, попробуй использовать решето Эратосфена! Уверен, это будет увлекательно и полезно!
Как использовать решето Эратосфена

Давайте поговорим о решете Эратосфена. Надеюсь, вы когда-нибудь слышали об этом великом математическом методе. Если нет, не беда! Я расскажу вам, как использовать решето Эратосфена и как оно может помочь вам в поиске простых чисел.
Итак, что такое решето Эратосфена? Оно является древнейшим известным методом для нахождения всех простых чисел до заданного числа. Но как оно работает?
Основная идея решета Эратосфена заключается в следующем: мы начинаем с заданного числа и перечисляем все числа до этого числа. Затем мы исключаем все числа, которые делятся на другие числа, оставляя только простые числа.
Представьте себе, что вы имеете длинную полоску бумаги, на которую вы наносите все числа до заданного числа. Затем вы начинаете зачеркивать числа, начиная с двойки (потому что двойка — это первое простое число). Вы зачеркиваете все числа, которые делятся на два. Затем вы переходите к тройкам и зачеркиваете все числа, которые делятся на три. И так далее.
В конечном итоге у вас останутся только простые числа на вашей полоске бумаги. Вот и все! Вы успешно использовали решето Эратосфена для нахождения простых чисел.
Теперь, давайте представим, что мы хотим найти все простые числа до 100. Мы можем использовать решето Эратосфена, чтобы сделать это в несколько простых шагов. Заходите, присаживайтесь и посмотрим, как это делается!
Пример использования решета Эратосфена
Представьте, вы организовываете большую вечеринку с друзьями и хотите пригласить только простые числа. Вместо того, чтобы проверять каждое число на простоту вручную, можно воспользоваться решетом Эратосфена. Это очень эффективный метод для нахождения всех простых чисел до заданного числа.
Как это работает? Допустим, вы хотите найти все простые числа до 30. Вы начинаете с таблицы чисел от 2 до 30 и начинаете зачеркивать числа, которые являются кратными другим числам. Например, 2 — простое число, поэтому вы заносите его в список простых. Затем вы зачеркиваете все числа, кратные 2 (4, 6, 8, 10 и т.д.). Затем вы переходите к следующему незачеркнутому числу, 3, и повторяете процесс.
В конечном итоге, все незачеркнутые числа являются простыми. В нашем примере, они будут выглядеть так: 2, 3, 5, 7, 11, 13, 17, 19, 23 и 29. И это только до 30! Вы можете использовать решето Эратосфена, чтобы найти все простые числа до любого заданного числа, и это значительно упрощает процесс проверки на простоту.
Таким образом, решето Эратосфена — это простой и эффективный способ нахождения всех простых чисел, и его можно использовать во множестве задач, где требуется проверка простоты чисел. Например, при поиске простых чисел в заданном диапазоне или при проверке чисел на простоту в криптографических алгоритмах.
Сложность алгоритма решета Эратосфена

Оценка сложности алгоритма решета Эратосфена составляет O(N log log N), что является весьма эффективным с теоретической точки зрения. В худшем случае, время выполнения алгоритма будет примерно квадратичным, O(N^2), если требуется вычислить все простые числа до N.
Решето Эратосфена является одним из самых быстрых и проверенных способов нахождения простых чисел. Оно может использоваться в широком спектре задач, требующих работы с простыми числами, таких как криптография, теория чисел и даже оптимизация кода.