Решето в математике — это инструмент, который помогает найти все простые числа до заданного числа. В основе его работы лежит простая идея: удалять из списка все числа, которые являются кратными уже найденным простым числам. Поэтому решето особенно полезно при поиске простых чисел больших величин, так как позволяет существенно сократить количество проверок. Для использования решета необходимо знать, как работает алгоритм, а также уметь программировать для автоматизации этого процесса.
Определение решета
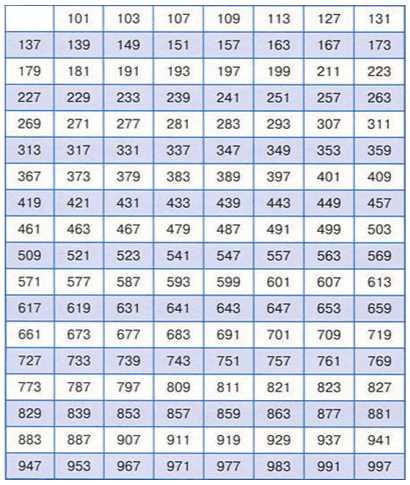
Когда мы говорим о числах, то есть два типа: простые и составные. Простые числа – это те числа, которые не делятся на что-то кроме себя и единицы. А составные числа – это числа, которые имеют делители помимо себя и единицы.
Так вот, решето – это инструмент, который помогает нам быстро и эффективно найти все простые числа в заданном диапазоне. Он работает следующим образом: сначала мы отмечаем все числа в диапазоне, а затем последовательно исключаем числа, которые являются составными, оставляя только простые числа.
Преимущество использования решета в поиске простых чисел заключается в его эффективности. Оно позволяет нам избежать лишних вычислений и сократить время выполнения задачи. Именно поэтому решето является одним из важных инструментов в математике и алгоритмике.
Принцип работы решета

Ты когда-нибудь задумывался, как работает решето? Давай разберемся вместе!
Решето — это математический инструмент, который помогает нам находить простые числа. Простые числа — это числа, которые делятся только на 1 и на себя самого.
Итак, как работает решето? Допустим, у нас есть последовательность чисел от 2 до 20. Мы начинаем с самого маленького числа — 2, и вычеркиваем все числа, которые делятся на 2. В результате у нас остаются только числа 2, 3, 5, 7, 11, 13, 17 и 19.
Теперь мы берем следующее невычеркнутое число — 3, и снова вычеркиваем все числа, которые делятся на 3. Продолжаем этот процесс, пока не вычеркнем все числа.
Принцип работы решета основан на том, что если число делится на другое число, то оно не является простым числом. Поэтому мы постепенно вычеркиваем все составные числа, оставляя только простые числа.
И вот мы получили наши простые числа: 2, 3, 5, 7, 11, 13, 17 и 19. Теперь мы можем использовать их для решения различных математических задач.
Так что, решето — это очень полезный инструмент, который помогает нам находить простые числа. Надеюсь, этот принцип работы решета стал для тебя понятен. Если у тебя есть вопросы, не стесняйся задавать!
Примеры использования решета
Вот несколько примеров:
- Проверка чисел на простоту: Если вам нужно узнать, является ли данное число простым, решето может пригодиться. Просто примените решето Эратосфена, чтобы найти все простые числа до заданного числа. Если число встречается в списке простых чисел, то оно составное, иначе — простое.
- Генерация простых чисел: Если вам нужно сгенерировать набор простых чисел в определенном диапазоне, решето Эратосфена может прийти на помощь. Примените решето к диапазону чисел и получите список простых чисел, которые находятся в этом диапазоне.
- Шифрование и декодирование: В криптографии решето применяется для шифрования и декодирования сообщений. Например, можно использовать решето Эратосфена для генерации ключей шифрования. Затем, с помощью полученных ключей можно шифровать и дешифровать сообщения.
Это всего лишь некоторые примеры использования решета в повседневной жизни. Надеюсь, теперь вы понимаете, что решето может быть полезным инструментом в различных ситуациях, связанных с числами и шифрованием.
История развития решета
Аристотель (384 г. до н. э. – 322 г. до н. э.) был одним из первых ученых, которые использовали решето для выявления простых чисел. Он разработал простейший алгоритм с использованием простого решета.
Эратосфен (около 276 г. до н. э. – около 194 г. до н. э.) внес значительный вклад в развитие решета. Он известен как создатель «решета Эратосфена» — более сложного алгоритма, основанного на простом решете Аристотеля.
В дальнейшем, многие математики, включая Коперника (1473–1543), Ходженса (1546–1608) и Ньютон (1643–1727), разрабатывали и модифицировали решето для более эффективного отбора простых чисел.
Современное решето Эратосфена — это алгоритм, основанный на идее решета Эратосфена, но с использованием современных вычислительных возможностей. Оно является одним из быстрых и эффективных способов отбора простых чисел и широко применяется в современной математике и информатике.
История развития решета демонстрирует, каких успехов в математике можно достичь благодаря сотрудничеству и совместным усилиям ученых разных времен и эпох. Благодаря их усилиям решето стало одним из ключевых инструментов в алгебре, теории чисел и информатике.