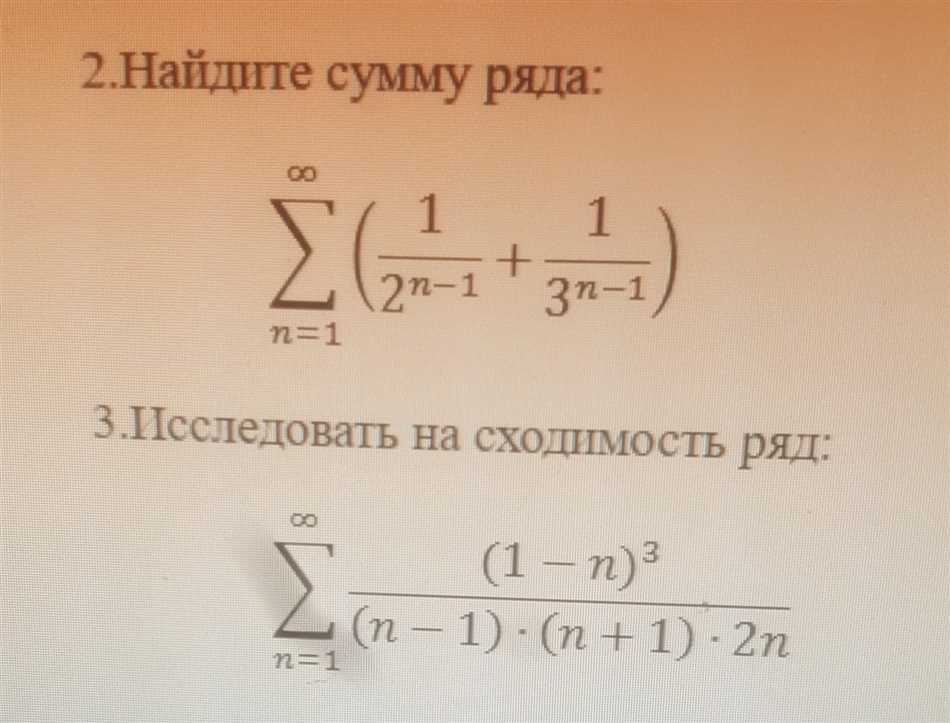
Когда мы говорим о математике, ряд это последовательность чисел, которая упорядочена согласно определенному правилу. Эта концепция является ключевой в алгебре и анализе. Ряды в математике позволяют нам суммировать бесконечное количество чисел и представляют собой мощный инструмент для решения различных задач.
В ряде каждый номер является обобщением предыдущего числа. Таким образом, мы можем использовать это правило для нахождения следующего номера в ряде. Ряды помогают нам изучать поведение числовых последовательностей и прогнозировать их значения.
Изучая ряды, мы можем определить их сходимость или расходимость. Сходимость означает, что ряд имеет конечную сумму, тогда как расходимость означает, что сумма ряда стремится к бесконечности.
Ряды являются одним из фундаментальных понятий математики и имеют широкое применение в различных областях, от физики и экономики до статистики и компьютерных наук.
Определение ряда
Ряды могут быть различными: сходящимися и расходящимися. Сходящийся ряд — это ряд, у которого сумма его членов принимает определенное значение. Например, сумма ряда 1/2 + 1/4 + 1/8 + 1/16 + … равна 1. Такой ряд называется геометрической прогрессией.
С другой стороны, ряд называется расходящимся, если сумма его членов стремится к бесконечности или не имеет определенного значения. Например, ряд 1 + 2 + 3 + 4 + … является расходящимся, так как его сумма бесконечна.
Ряды имеют множество приложений в математике и других науках. Они используются для моделирования реальных процессов, описания бесконечных множеств и анализа функций. Нахождение суммы ряда является важной задачей в математике и может потребовать использования различных техник и методов. Ряды также играют важную роль в образовании, помогая студентам развивать логическое и аналитическое мышление, а также улучшать навыки решения проблем.
Сумма ряда
Поговорим о сумме ряда. Если ты знаком с понятием ряда в математике, то, наверняка, знаешь, что это последовательность чисел, упорядоченная в определенном порядке. А что такое сумма ряда? Это сумма всех чисел этой последовательности.
Давай рассмотрим простой пример. Рассмотрим ряд, в котором каждое следующее число больше предыдущего на 2: 2, 4, 6, 8, 10… Если мы захотим найти сумму первых 5 чисел этого ряда, то просто сложим их: 2 + 4 + 6 + 8 + 10 = 30. Вот и вся сумма ряда!
Бывает, что ряды имеют особое свойство, называемое «сходящимся» или «расходящимся». Скажи, есть ли в ряду 1, 2, 3, 4, 5… сумма? Нет, ее нет, потому что этот ряд бесконечен и числа в нем все время растут. Такой ряд называется «расходящимся».
Но не волнуйся, ряды бывают и сходящиеся! Они имеют конечную сумму. Например, ряд 1/2, 1/4, 1/8, 1/16, 1/32… имеет сумму 1. Замечательно, верно? Постепенно, с каждым новым числом, мы все ближе и ближе подходим к числу 1.
Так что, внимание, готовься, складывай числа ряда и находи их сумму! Она может быть конечной или бесконечной – в этом вся прелесть математики!
Сходящийся ряд
Для того чтобы понять, что такое сходящийся ряд, давайте представим, что у нас есть большое количество чисел, и мы складываем их все вместе. Если сумма этих чисел, полученная путем сложения, стремится к конечному числу, то говорят, что ряд сходится.
Но как понять, сходится ли ряд или нет? Существует несколько методов для определения сходимости ряда, таких как критерий сравнения и критерий Даламбера. Но самое важное для понимания сходящегося ряда — то, что при бесконечном сложении чисел его сумма будет ограничена.
Представьте, что вы собираете монеты каждый день. Первый день вы находите 1 монету, второй — 2 монеты, третий — 3 монеты и так далее. Если вы будете складывать все найденные монеты, то их сумма будет увеличиваться с каждым днем. Но если вы складываете бесконечное количество монет, то сумма будет ограничена, например, 100 монетами.
Итак, сходящийся ряд — это ряд, чья сумма ограничена и не бесконечно возрастает. Важно понимать, что сходимость ряда может быть очень важной в математике, а также в других областях науки, таких как физика и экономика.
Расходящийся ряд
Давай рассмотрим пример: ряд 1+2+3+4+5+… Этот ряд является расходящимся, потому что сумма его членов будет бесконечно возрастать. Каждый следующий член будет больше предыдущего, и их сумма будет стремиться к бесконечности.
Почему расходящиеся ряды важны? Они помогают нам понять, какие последовательности чисел можно складывать бесконечное количество раз и получать конечную или бесконечную сумму. Использование расходящихся рядов позволяет нам решать сложные математические проблемы и применять их в разных областях науки и техники.
Знание о расходящихся рядах помогает нам понять, почему иногда невозможно сложить бесконечное количество чисел и получить конечную сумму. Это важный принцип в математике и более широко применяется в научных исследованиях и практических проблемах.
Абсолютно сходящийся ряд
Эй, знаешь ли ты, что такое абсолютно сходящийся ряд? У нас есть обычные ряды, знаешь ли, те, которые сходятся, и некоторые из них могут сходиться абсолютно! Это звучит удивительно, правда? Давай разберемся, что это такое.
Когда мы говорим, что ряд абсолютно сходится, мы имеем в виду, что сумма абсолютных значений его членов сходится. Для нас это означает, что все положительные и отрицательные значения в ряду приносят дополнительные суммы и в конечном итоге они все сокращаются. В результате получается сумма, которая сходится.
Такой тип ряда часто используется в математике, особенно в анализе функций. Он дает нам больше информации о сходимости, потому что даже если ряд исходно не сходится, если его абсолютные значения сходятся, то мы можем сказать, что он абсолютно сходится и имеет конечную сумму.
Интересно, правда? Я люблю, когда математика раскрывает перед нами такие величественные идеи. Так что следующий раз, когда ты услышишь о абсолютно сходящемся ряде, не забудь, что это просто ряд, чьи абсолютные значения сходятся, и он может иметь конечную сумму. Вот так-то!
Условно сходящийся ряд
Такой ряд может иметь две основные категории сходимости: абсолютную и условную. При абсолютной сходимости сумма ряда будет одинаковой, независимо от порядка слагаемых. В случае условной сходимости сумма ряда будет зависеть от конкретного порядка слагаемых.
Примером условно сходящегося ряда является ряд Лейбница:
- Ряд Лейбница имеет вид: 1 — 1/3 + 1/5 — 1/7 + …
- Этот ряд сходится, так как его общий член стремится к нулю.
- Однако, при суммировании его членов в различных порядках, можно получить разную сумму.
Условно сходящиеся ряды представляют особый интерес в математике и имеют множество практических применений. Изучение их свойств и поведения позволяет более глубоко понять природу сходимости рядов и развивать методы их анализа и расчета.




