Что такое рост в квадрате — понятие и причины его возникновения

Знакома с термином «рост в квадрате»? Это понятие из математики, которое объясняет замечательное свойство чисел. Когда число умножается на себя, результатом является его квадрат. Например, квадрат числа 5 равен 25, так как 5 * 5 = 25.

Понять, что такое рост в квадрате, поможет ежедневная жизнь. Применяется он во многих сферах. Например, в физике для расчета площади квадрата или прямоугольника. В географии, чтобы определить площадь территории. А в экономике рост в квадрате связан с прогрессией, а значит с увеличением дохода.

Теперь, когда ты знаешь, что такое рост в квадрате, можешь применять этот принцип в различных областях и удивлять своими знаниями окружающих!

Определение роста в квадрате

Наверняка каждый из нас слышал выражение «рост в квадрате». Но что же это такое и как его определить?

Рост в квадрате — это математическая операция, при которой значение числа умножается само на себя. В основном, это относится к измерению роста человека. Если, например, у нас есть рост в метрах, то для определения роста в квадрате нужно умножить значение на себя. Таким образом, мы получим площадь, которую занимает наш рост на плоскости.

Зачем нам нужно знать рост в квадрате? Это может быть полезно, например, при расчете индекса массы тела (ИМТ). ИМТ вычисляется путем деления массы тела на рост в квадрате. Таким образом, зная рост в квадрате, мы можем оценить, насколько нам нужно изменить свою массу, чтобы достичь оптимального веса.

Кроме того, знание своего роста в квадрате может помочь нам более осознанно относиться к своему здоровью и физической форме. Это может стать стимулом для занятий спортом или поддержания активного образа жизни.

Итак, знать свой рост в квадрате — это не только интересный математический факт, но и полезная информация для личного здоровья и оценки физической формы. Берите меры и изучайте мир вокруг себя!

Математическая формула роста в квадрате

Когда речь заходит о росте в квадрате, мы обычно говорим о формуле для вычисления площади квадрата. Квадрат имеет четыре равные стороны и все углы прямые. Его площадь можно найти, умножив длину одной из сторон на себя.

Формула выглядит так:

Площадь квадрата = сторона × сторона

Допустим, у нас есть квадрат со стороной 5 см. Чтобы найти его площадь, мы просто умножим 5 на 5 и получим 25 см². Вот и вся формула!

Теперь представь, что у нас есть семена, и мы собираемся выращивать растения. Мы знаем, что при правильном уходе они будут расти. Но какой будет их рост со временем?

Здесь мы можем использовать математическую формулу роста в квадрате для предсказания их будущего размера. Если изначально растение имеет размер a, то через некоторое время его размер будет a в квадрате.

Например, если изначальный размер растения составляет 2 см, то через некоторое время его размер будет 2 в квадрате, то есть 4 см². Из этого следует, что размер растения удваивается при использовании формулы роста в квадрате.

Таким образом, формула роста в квадрате позволяет нам предсказать, как будет изменяться размер чего-либо с течением времени. Используйте ее, чтобы проникнуть в магию математики и попробовать предсказать размеры своих растений или любого другого объекта, который растет!

Примеры практического применения роста в квадрате

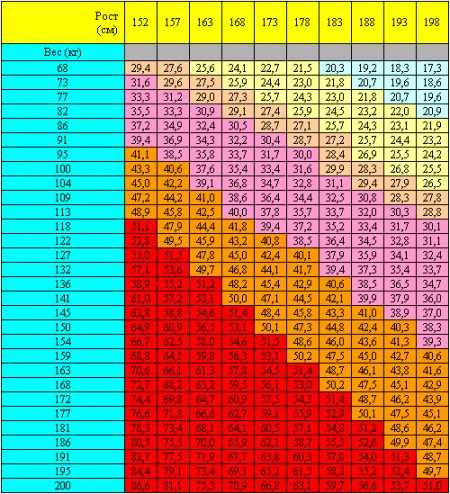
Рассмотрим несколько примеров практического применения роста в квадрате:

1. Физика: Рост в квадрате используется для вычисления кинетической энергии объекта с помощью формулы E = 1/2 mv^2, где m — масса объекта, а v — его скорость. Также рост в квадрате применяется для расчетов силы тяжести или для определения времени падения объекта с заданной высоты.
2. Инженерия: В инженерии рост в квадрате используется для расчета давления жидкости или газа в трубопроводах или системах, а также для определения силы давления ветра на конструкции зданий или мостов.
3. Финансы: В финансовой сфере рост в квадрате может быть использован для расчетов процентов или ставки роста вклада или инвестиций. Например, для составления графика роста капитала в течение определенного периода времени.

Это лишь некоторые примеры применения роста в квадрате, и на самом деле список возможностей этой математической операции довольно обширен. Понимание и умение использовать это понятие может быть полезным в различных сферах жизни, образования и науки.