Что такое ротор в физике: простое объяснение

В физике мы часто слышим о терминах, которые кажутся сложными и непонятными. Один из таких терминов — «ротор». Что же это такое? Давайте разберемся.

Ротор, или векторный оператор, используется для описания движения и вращения тел. Он позволяет измерять скорость и направление вращения объекта. Грубо говоря, ротор показывает, как быстро и в каком направлении вращается что-то.

Чтобы лучше понять это понятие, представьте себе вращающуюся катушку ниток. Если вы будете наблюдать, то заметите, что нитки вокруг катушки вращаются со своей скоростью и в определенном направлении. Вот эта скорость и направление вращения — это и есть ротор.

Теперь вы знаете, что такое ротор в физике. Он помогает нам понять вращение и движение объектов в пространстве. Используя ротор, физики могут решать разнообразные задачи, связанные с вращением и механикой.

Ротор: определение и основные понятия

В обычной жизни мы можем столкнуться с роторами в различных контекстах. Например, когда стоишь возле вентилятора и чувствуешь поток воздуха, это воздушный поток можно представить векторным полем, а его вихревые свойства – именно ротором. А что насчет вихря в воде, который образуется, когда камень падает в пруд? И это тоже ротор!

Если мы говорим о математической стороне, то ротор определен как векторное произведение градиента исходной функции. И, знаешь, это связано с понятием циркуляции векторного поля. Циркуляция – это замкнутый интеграл вдоль кривой, который измеряет вращательные свойства поля в вихревых точках.

Так что, ротор – это способ определить вихревые свойства векторного поля, будь то воздушный поток или движение жидкости. И, честно говоря, математика за этим стоит довольно интересная! Так что следующий раз, когда столкнешься с ротором, вспомни, что он помогает нам лучше понять вихревые явления вокруг нас!

Формулировка ротора через частные производные

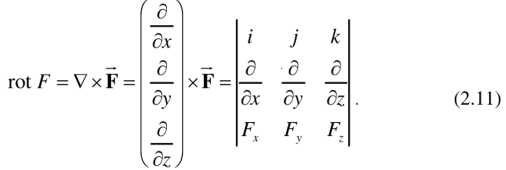
Формулировка ротора через частные производные гласит, что ротор векторного поля определяется как векторное произведение градиента поля и ортогонального базиса.

Позвольте мне объяснить это понятным примером. Представьте, что у вас есть поле, в котором каждая точка имеет векторное направление. Если вы возьмете маленькую замкнутую кривую в этом поле, то ротор будет показывать, как сильно и в каком направлении вихрь связанный с этой кривой.

Если вы совершите круговое движение по кривой, ротор будет определять интенсивность и направление вращения. Если он равен нулю, то поле не вращается в окружности, а если он отличен от нуля, то имеется вращение.

Таким образом, формулировка ротора через частные производные позволяет более точно описывать вращение векторных полей в пространстве.

Свойства и особенности ротора

Одной из основных особенностей ротора является его способность к вращению вокруг своей оси. Благодаря этому свойству, ротор может приводить в движение другие части механизма и выполнять различные функции.

Кроме того, ротор обладает высокой прочностью и устойчивостью к износу. Это позволяет ему работать на протяжении длительного времени без поломок и потери производительности.

Ротор также может быть изготовлен из различных материалов, в зависимости от требований и целей механизма. Например, в автомобильных двигателях часто используются роторы из сплавов алюминия или стали, из-за их легкости и прочности.

Одной из интересных особенностей ротора является возможность изменять его скорость вращения. Это позволяет регулировать работу механизма в зависимости от необходимости и достичь наилучших результатов.

Также, ротор может быть использован в различных областях промышленности, включая электронику, авиацию, механику и другие. Благодаря своим уникальным свойствам и возможностям, ротор стал неотъемлемой частью современных технологий и устройств.

Геометрическое представление ротора

Представьте себе, что вы водитель маленького лодочного мотора. Вы крутите рукоять, и вал мотора запускает вращение пропеллера, который толкает лодку вперед. Но что происходит, когда вы отпускаете рукоять? Именно здесь и вступает в действие понятие ротора в физике.

Ротор — это векторное поле, которое представляет собой вращение вокруг точки. В геометрическом представлении ротор можно представить, как «вихрь» в пространстве. Если взять кусок бумаги и смазать на него немного краски, а затем начать вращать его, вы увидите, что краска начинает образовывать круговые следы. Точка, вокруг которой происходит вращение, и будет центром вихря.

В физике ротор имеет большое значение, так как он связан с понятием «вихревого потока». Вихревой поток может возникать в различных ситуациях, таких как обтекание тела воздухом или водой. Когда вихревой поток формируется, его величину и направление можно определить с помощью ротора.

Надеюсь, я смог объяснить вам геометрическое представление ротора. Если у вас есть какие-либо вопросы, пожалуйста, спросите! Я всегда рад помочь

Закон сохранения ротора

Закон сохранения ротора гласит, что если ротор векторного поля равен нулю в начальный момент времени, то он сохраняется в течение всего процесса. Иными словами, если вихри в поле невозможны в начале, они не могут возникнуть искусственно или через пространственные изменения.

Этот закон является следствием уравнений Максвелла в электромагнитной теории и позволяет нам понять, что электромагнитные поля не могут быть источником течения энергии или материи. Таким образом, сохранение ротора является важным принципом, который позволяет нам понять и объяснить многие физические явления, связанные с векторными полями.

Примеры применения ротора в физике

1. Электромагнетизм

В электромагнетизме ротор используется для описания магнитных полей. По теореме Стокса ротор векторного поля равен замкнутости его интеграла по произвольной замкнутой кривой. Таким образом, ротор позволяет определить силовые линии магнитного поля и направление его изменения.

2. Гидродинамика

В гидродинамике ротор используется для описания вращательного движения жидкости. Например, в законе сохранения массы для несжимаемой жидкости ротор скорости определяет величину и направление вихревого движения в жидкости.

3. Квантовая механика

В квантовой механике ротор оператора координатной функции применяется для описания спиновых состояний частиц. Он позволяет определить магнитный момент и вращательную симметрию системы.

• Электромагнетизм
• Гидродинамика
• Квантовая механика

Все эти примеры демонстрируют универсальность и важность использования ротора в физике. Он помогает описывать различные физические явления и является неотъемлемым инструментом для анализа и понимания физических систем.