Что такое сечение параллелепипеда – понятие и примеры

Когда мы говорим о сечении параллелепипеда, мы имеем в виду плоскую фигуру, которая образуется, когда прямоугольный параллелепипед пересекается плоскостью.

Сечение может быть различной формы — это может быть круг, эллипс, треугольник, прямоугольник или любая другая фигура, в зависимости от положения и ориентации плоскости. Когда плоскость пересекает параллелепипед, она отрезает его часть, создавая сечение.

Сечение параллелепипеда является важным понятием в геометрии и строительстве. Оно позволяет нам анализировать и понимать структуру и форму параллелепипеда, а также использовать его для создания сложных конструкций и моделей.

Например, при проектировании здания архитекторы и инженеры часто используют сечения параллелепипедов, чтобы лучше представлять себе расположение комнат и подсчитывать площадь пола и стен.

Основные принципы сечения параллелепипеда

Принцип сечения параллелепипеда заключается в том, что плоскость проходит через параллелепипед, разделяя его на две части. Важно отметить, что плоскость может проходить как внутри параллелепипеда, так и между его гранями.

Представь, что у тебя есть большой кусок сыра, и ты режешь его на кубики. Каждый кубик — это сечение параллелепипеда. В зависимости от угла, под которым ты режешь сыр, сечение может быть прямоугольным, квадратным или даже треугольным. Это все зависит от того, как размещена плоскость относительно параллелепипеда.

Геометрическое определение сечения

Сечение может быть как плоским, так и неплоским. Если плоскость идеально пересекает все стороны параллелепипеда, оно будет плоским сечением. Однако, если плоскость не пересекает все стороны параллелепипеда, то полученное сечение будет неплоским и может иметь различную форму. Неплоское сечение может быть треугольным, прямоугольным или даже криволинейным.

Геометрическое определение сечения является важным понятием в математике и инженерии. Оно помогает нам понять формы и структуру объектов, а также применять их для решения различных задач. Однако, в повседневной жизни мы не всегда задумываемся о геометрии сечений. Есть так много других увлекательных вещей, которыми мы можем заняться!

Виды сечений параллелепипеда

1. Сечение параллельное одной из граней: в этом случае, плоскость проходит параллельно одной из граней параллелепипеда и пересекает его в параллелограмме.

2. Сечение через диагональ: плоскость проходит через диагональ параллелепипеда и пересекает его в треугольнике или пятиугольнике.

3. Сечение перпендикулярное грани: плоскость пересекает параллелепипед перпендикулярно одной из его граней. В этом случае, сечение будет являться параллелограммом.

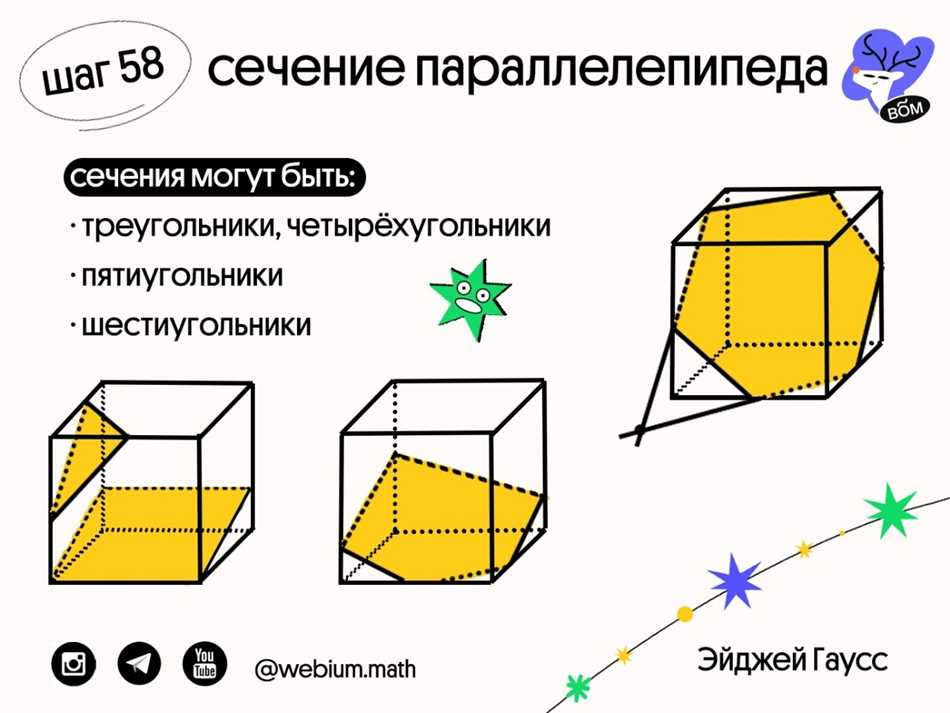
4. Сечение под углом к грани: плоскость пересекает параллелепипед под углом к одной из его граней. В зависимости от угла, получится треугольник, пятиугольник или шестиугольник.

Различные виды сечений параллелепипеда могут иметь разные формы и размеры, в зависимости от положения плоскости относительно фигуры. Знание видов сечений полезно для изучения геометрии и решения различных задач, связанных с параллелепипедами.

Горизонтальные сечения

Когда сечение проходит по верхней грани параллелепипеда, например, вы получите круглое сечение. Знаете почему? Потому что верхняя грань параллелепипеда – это прямоугольник, а круг – это просто прямоугольник со скругленными углами! Вот таким неожиданным образом математика встречается с геометрией.

А если сечение проходит выше середины, но ниже верхней грани параллелепипеда, то получится овалообразная фигура. Интересно, да? Такие горизонтальные сечения позволяют нам увидеть разные формы и фигуры, которые скрываются внутри параллелепипеда.

Вертикальные сечения

Вертикальные сечения — это плоскости, которые пересекают параллелепипед снизу вверх или сверху вниз. Здорово, да? Они позволяют нам увидеть, что находится внутри этого таинственного объемного объекта.

Давай представим, что параллелепипед — это огромный кусок сладкого пирога, а вертикальные сечения — это разрезы, которые позволяют взглянуть на его слои. Какой слюнявчик течет?

Так что, будучи на физике, не забывай заглядывать внутрь всего, что окружает тебя. Вертикальные сечения помогут тебе увидеть, что скрыто внутри объемных фигур и принести новые открытия в твою жизнь. Сечения — это волшебство, которое позволяет нам узнавать и понимать мир лучше. Интересно, какой еще объект можно исследовать с помощью сечений?

Диагональные сечения

Когда мы говорим о сечении параллелепипеда, мы обычно представляем себе это как двумерную плоскость, которая пересекает фигуру и отделает от нее некоторую часть. Но что если мы хотим сделать сечение по-другому? А вот и ответ: диагональные сечения!

Диагональное сечение — это особый вид сечения, которое проходит через параллелепипед по его диагонали. Как правило, диагональное сечение создает отличные от прямолинейных сечений формы. Оно может образовывать интересные геометрические фигуры, например, треугольники, которые имеют острые углы или параллелограммы с неправильными сторонами и углами.

Диагональные сечения могут использоваться для создания уникальных и необычных дизайнов или украшений. Например, если вы работаете в области архитектуры или дизайна интерьера, вы можете использовать диагональные сечения, чтобы добавить оригинальность и креативность вашим проектам.

Свойства сечений параллелепипеда

• Форма: Сечение параллелепипеда может иметь различную форму в зависимости от положения и угла плоскости относительно осей параллелепипеда. Это может быть круг, эллипс, прямоугольник или другая фигура.
• Площадь: Площадь сечения параллелепипеда зависит от положения плоскости и ее формы. Чем ближе плоскость к одной из сторон параллелепипеда, тем больше площадь сечения.
• Периметр: Периметр сечения параллелепипеда также зависит от формы и положения плоскости. Если плоскость пересекает боковую грань параллелепипеда под прямым углом, то периметр сечения будет равен периметру этой грани параллелепипеда.
• Соотношение сторон: Соотношение сторон сечения может быть разным и зависит от угла, под которым плоскость пересекает стороны параллелепипеда. Если плоскость пересекает стороны под прямым углом, то соотношение сторон совпадает соотношением сторон самого параллелепипеда.

Интересно, правда? Сечения параллелепипеда могут иметь разнообразные формы и свойства, в зависимости от их положения и угла относительно параллелепипеда. С увлекательными математическими объектами, всегда есть что-то новое для изучения и открытия. Какие еще интересные факты ты знаешь о сечениях параллелепипеда?

Применение сечений параллелепипеда в реальной жизни

1. Архитектура и строительство. Сечения параллелепипеда играют важную роль в проектировании и строительстве зданий. Они позволяют определить форму и размеры помещений, расположение окон, дверей, а также помогают оценить пропорции и гармоничность архитектурных решений.

2. Объемные модели. При создании объемных моделей, таких как макеты зданий, машин, аппаратов и других объектов, сечения параллелепипеда используются для выделения отдельных элементов конструкции и отображения внутренних деталей.

3. Инженерия и конструирование. В инженерии и конструировании сечения параллелепипеда применяются при проектировании машин и механизмов, определении прочности и устойчивости материалов, расчете объемов и массы конструкций.

4. География и картография. В географии и картографии сечения параллелепипеда используются для отображения рельефа местности на топографических картах, создания трехмерных моделей ландшафта и определения высотных данных.

5. Медицина. В медицинской диагностике сечения параллелепипеда применяются для создания срезов органов и тканей при проведении компьютерной и магнитно-резонансной томографии. Это позволяет врачам получить детальную информацию о внутренней структуре тела пациента и построить трехмерную модель органа.