Что такое синусы и косинусы: основные понятия и применение

Синусы и косинусы – это функции, которые используются в математике и физике для описания колебаний и волн. Они являются основными тригонометрическими функциями и применяются во множестве научных и инженерных расчетов.

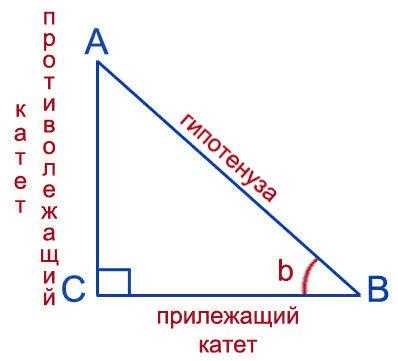
Синус и косинус являются отношениями сторон прямоугольного треугольника, которые зависят от угла, образованного этими сторонами и гипотенузой. Синус угла равен отношению противолежащего катета к гипотенузе, а косинус – отношению прилежащего катета к гипотенузе.

Синусы и косинусы применяются в различных областях, включая физику, инженерию, компьютерную графику, астрономию и многое другое. Их использование позволяет точно описывать и анализировать различные процессы и явления, связанные с колебаниями и волнами.

Изучение синусов и косинусов

Синус и косинус — это тригонометрические функции, которые связаны с прямоугольными треугольниками. Они представляют собой соотношения между сторонами треугольника и углами в нем. В математике эти функции обозначаются как sin и cos.

Зачем же нам изучать синусы и косинусы? Они помогают нам решать множество задач. Например, с их помощью мы можем вычислить длину противолежащей стороны или высоту треугольника, если известны длина основания и один из углов. Также синусы и косинусы используются для решения задач геометрии, физики, инженерии и даже в программировании.

Чтобы понять, как работают синусы и косинусы, давай рассмотрим пример. Представь, что ты находишься на берегу озера и смотришь на луну. У тебя есть прямоугольный треугольник: твое местоположение — угол, противолежащая сторона — расстояние до луны, основание — горизонтальное расстояние до луны. Синус угла будет отражать вертикальное расстояние до луны, а косинус — горизонтальное.

Изучение синусов и косинусов может быть интересным и полезным. Тебе понадобятся некоторые математические навыки и практика, но с ними ты сможешь использовать эти функции для решения сложных задач. Попробуй применить их в своей жизни или работе — кто знает, может быть, они помогут тебе взлететь выше небес!

Сущность тригонометрических функций

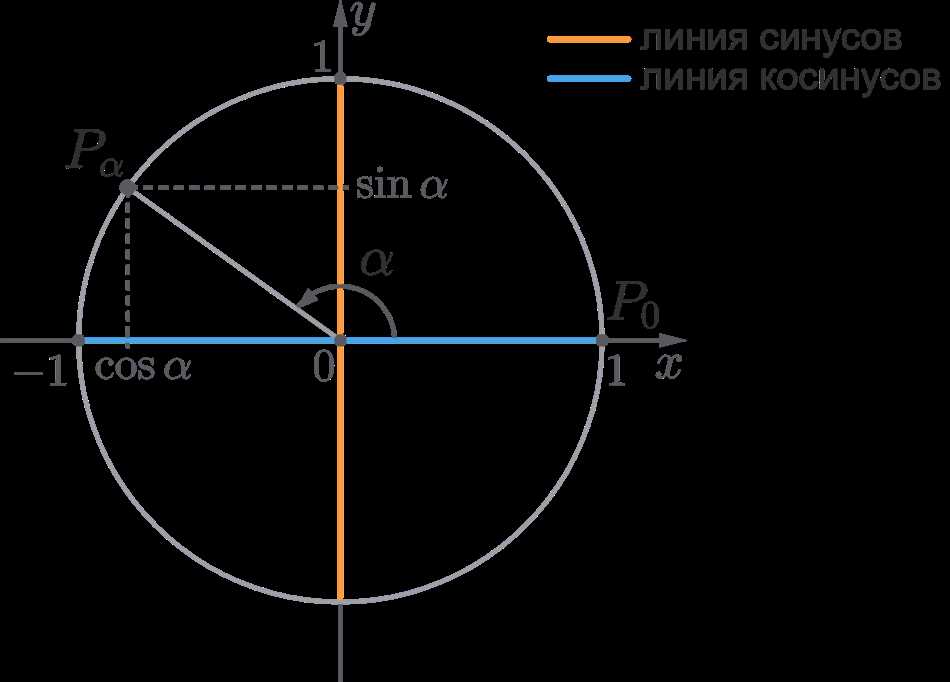
Допустим, у тебя есть треугольник с прямым углом, а угол между горизонтальной стороной и гипотенузой называется углом тета. Вот прямо на этом угле и сосредоточены синус и косинус.

Синус угла тета определяется как отношение длины противолежащего катета к длине гипотенузы. А косинус угла – это отношение длины прилежащего катета к длине гипотенузы.

Зачем нам это нужно в реальной жизни? Ну, представь, ты лыжник и тебе нужно определить, насколько крутой склон. Здесь тригонометрические функции приходят на помощь. Они помогут тебе выразить крутизну склона в терминах угла наклона и помогут принять решение, по какому склону тебе спускаться.

Более того, синусы и косинусы находят свое применение в физике, инженерии, астрономии и многих других областях науки и техники. Они помогают нам решать различные задачи, связанные с углами и отношениями сторон треугольников.

Так что несмотря на то, что некоторые могут считать тригонометрию сложной и ненужной, она на самом деле очень полезна и универсальна. Ведь благодаря ей мы можем лучше понимать окружающий мир и решать разнообразные задачи! А как ты думаешь, есть ли у нас в жизни ситуации, где нам приходится использовать синусы и косинусы?

Применение синусов и косинусов

Одно из применений синусов и косинусов — это в физике. Они помогают нам понять и описать различные волны и колебания. Например, при изучении звуковых волн или электромагнитных колебаний мы используем синусы и косинусы для анализа и предсказания их характеристик.

Также синусы и косинусы находят применение в технике и инженерии. Они используются для расчета и проектирования различных систем, таких как электрические цепи, механизмы, антенны и многое другое. Например, при проектировании электрической цепи мы можем использовать синусоидальные функции для определения амплитуды и фазы сигнала.

Кроме того, синусы и косинусы находят применение в геометрии и геодезии. Они позволяют нам рассчитывать расстояния, высоты и углы между объектами, используя тригонометрические соотношения. Например, при измерении высоты здания с помощью теодолита мы используем тригонометрическую формулу, основанную на синусах и косинусах.

Как видите, синусы и косинусы имеют множество практических применений и являются важными инструментами для работы в различных научных и технических областях. Их использование позволяет нам более глубоко понимать и анализировать различные явления и является неотъемлемой частью нашего ежедневного опыта и работы.

Тригонометрические тождества

Один из самых основных тригонометрических тождеств — это тождество Пифагора, которое гласит: синус квадрата угла плюс косинус квадрата угла равны единице. Это можно представить в виде уравнения: sin^2(x) + cos^2(x) = 1. Это тождество легко запомнить, и оно будет полезным при решении различных задач.

Еще одно важное тождество — это тангенс суммы углов. Оно позволяет нам выразить тангенс суммы двух углов через тангенсы их отдельных углов. Аналогично, существуют тождества для синуса и косинуса суммы и разности углов.

Тригонометрические тождества не только помогают нам упростить вычисления, но также имеют широкое применение в физике, инженерии и других областях науки. Они помогают нам анализировать и моделировать различные физические и геометрические явления.

Узнавая и понимая тригонометрические тождества, мы расширяем наши математические навыки и открываем двери к новым знаниям и возможностям.

Графики синусов и косинусов

И знаете что захватывающее? Эти функции могут быть представлены в виде графиков! График синуса (обычно обозначается как sin(x)) выглядит как шелковистая волна, возвышающаяся и падающая в зависимости от угла. График косинуса (обычно обозначается как cos(x)) выглядит похожим образом, но отстает на 1/4 периода.

А вы когда-нибудь задумывались о том, для чего они используются? Ну, на самом деле, синусы и косинусы имеют широкое применение в различных областях науки и техники. Они помогают изучать колебания, волны, а также использоваться в компьютерной графике и анализе данных. Вот уж применение науки в повседневной жизни, не правда ли?

Итак, теперь вы знаете, что такое синус и косинус, и как выглядят их графики. И давайте будем открывать новые и захватывающие миры математики вместе!

Заключение

Тригонометрические функции, такие как синус и косинус, играют важную роль в математике и ее приложениях. Они позволяют нам описывать и анализировать поведение колебательных и периодических явлений, встречающихся в различных научных и инженерных областях.

Одним из основных применений тригонометрических функций является решение уравнений. С помощью синусов и косинусов мы можем определить значения неизвестных переменных в уравнениях, которые связаны с геометрическими или физическими задачами.

Также тригонометрические функции помогают нам в понимании треугольников и их свойств. С помощью синуса и косинуса мы можем вычислять длины сторон и углы треугольников, а также находить площади и объемы геометрических фигур.