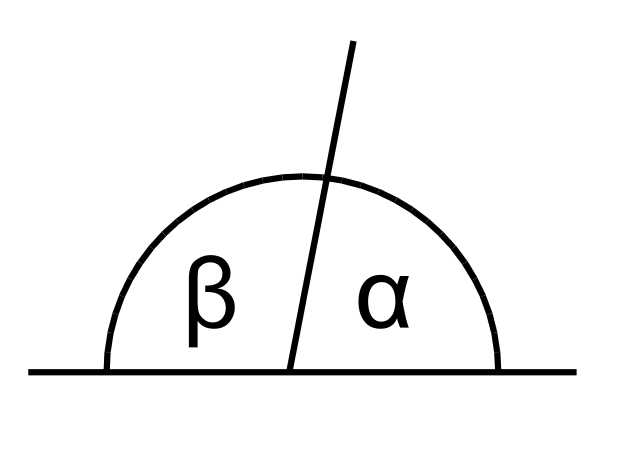
Смежные углы — это углы, которые имеют общую вершину и общую сторону. В математике смежные углы часто встречаются и играют важную роль при решении различных задач.
Они могут быть расположены как на прямых линиях, так и на пересекающихся. Смежные углы могут быть совпадающими, если они равны, или дополнительными, если их сумма равна 180 градусам.
Понимание смежных углов важно в геометрии и может помочь в решении задач по построению фигур или определению пропорций. Изучение смежных углов также важно при измерении и анализе углов в повседневной жизни.
Определение смежных углов
Чтобы понять лучше, представь себе, что у тебя есть прямая линия, а на ней расположены несколько углов. Смежные углы будут теми, которые лежат рядом друг с другом и имеют общую сторону. Например, если у тебя есть два угла: один меньше, а другой больше, при этом они имеют одну общую сторону и вершину, то это смежные углы.
Важно помнить, что смежные углы могут быть разного размера — один может быть острый, а другой тупой. Они могут быть дополнительными или смежными, и это влияет на их взаимоотношение. То есть, если два смежных угла являются дополнительными, их сумма будет составлять 180 градусов. А если углы смежные и смежные, их сумма будет составлять 90 градусов. Классно, правда?
Теперь, когда ты знаешь, что такое смежные углы, я уверен, что ты сможешь легко их определить и использовать в своих геометрических задачах. Примени свои знания и не забудь поделиться ими со своими друзьями — ведь знания еще никому не помешали!
Что такое смежные углы?
Зачем нам нужно знать про смежные углы? Ну, во-первых, они помогают нам различать и описывать геометрические фигуры. Например, если мы знаем, что углы около вершины квадрата или треугольника являются смежными, то мы можем использовать это свойство, чтобы найти значения других углов или решить геометрические задачи.
Кроме того, смежные углы играют важную роль в теории параллельных линий и углов. Если две пересекающиеся прямые образуют смежные углы, то их сумма будет равна 180 градусам, это свойство называется «сумма смежных углов». Это свойство позволяет нам решать различные задачи, связанные с параллельными линиями и углами, например, находить значения неизвестных углов.
Так что следующий раз, когда вы увидите два угла, расположенных рядом, задумайтесь о том, являются ли они смежными, и какие интересные свойства их можно использовать для решения задач геометрии. Успехов в изучении геометрии!
Свойства смежных углов
Основные свойства смежных углов включают:
- Сумма: Сумма двух смежных углов всегда равна 180 градусам. Это означает, что если у нас есть два смежных угла, мы можем сложить их значения и получить 180 градусов. Например, если один угол равен 60 градусам, то другой угол будет равен 120 градусам, чтобы их сумма составила 180 градусов.
- Дополнительность: Смежные углы, которые не являются смежными углами в прямой, называются дополнительными углами. Дополнительные углы в сумме дают 180 градусов.
- Линейность: Если имеется несколько смежных углов на одной линии, то их сумма также будет равна 180 градусам. Например, если имеется 3 смежных угла на одной линии, их сумма будет равна 180 градусов.
Знание свойств смежных углов позволяет нам решать задачи по геометрии, рассчитывать размеры углов и применять их в повседневной жизни, например, при монтаже мебели или строительстве.
Как определить смежные углы
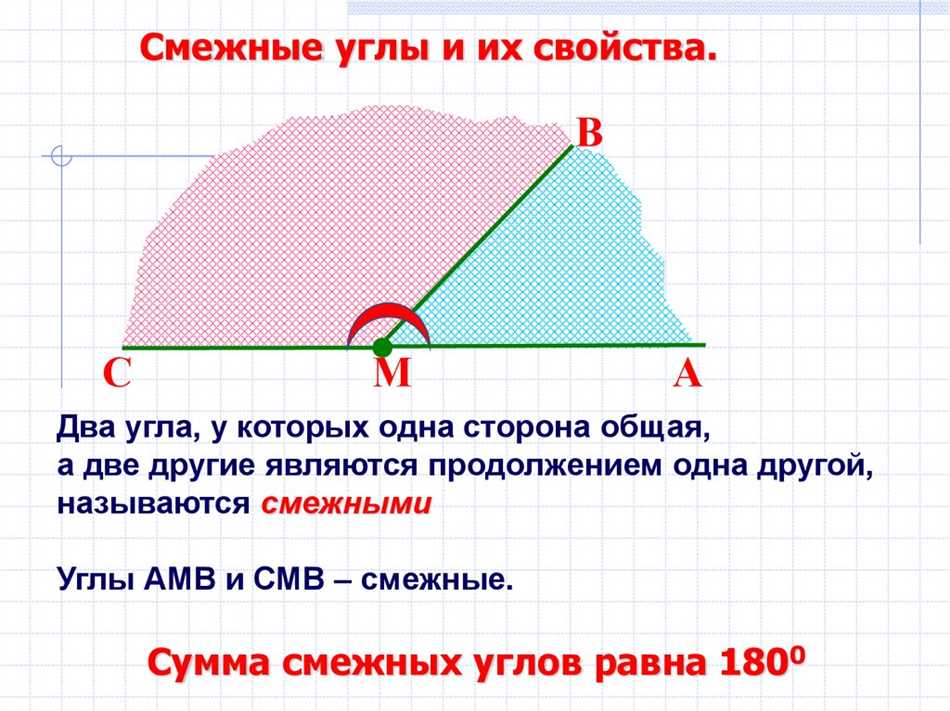
Про смежные углы я раньше ничего не слышал. Наверное, это какие-то особые углы? Ну, давай разбираться вместе. Возьмем лист бумаги и нарисуем две прямые линии, которые пересекаются в точке. Ой, я тут что-то нарисовал! Точка где-то выпала… Ничего, давай еще раз. Теперь взглянем на эти две линии. Заметьте, что они образуют несколько углов. И вот те, которые расположены рядом друг с другом и имеют общую сторону, называются смежными углами.
Легко запомнить: «смежные» означает «рядом». Так что, чтобы определить смежные углы, нужно найти два угла, которые находятся друг возле друга, имеют общую сторону, и оба лежат на разных прямых. Вообще, смежные углы похожи друг на друга: они равны между собой, если только прямые, на которых они лежат, пересекаются при прямом угле. Интересно, не правда ли?
Допустим, у нас есть две прямые линии, пересекающиеся в точке, и мы хотим найти смежные углы. Мы просто смотрим на углы, которые находятся рядом, с общей стороной, и вот — вуаля! Это смежные углы. Такая простая идея, но сколько в ней возможностей! Ведь смежные углы можно использовать в геометрии и вживую! Они помогут нам решить различные задачи, провести точные измерения и создать прекрасные сочинения искусства. Расскажи своим друзьям о смежных углах и посмотрите, как они удивятся и восхитятся!
Примеры использования смежных углов
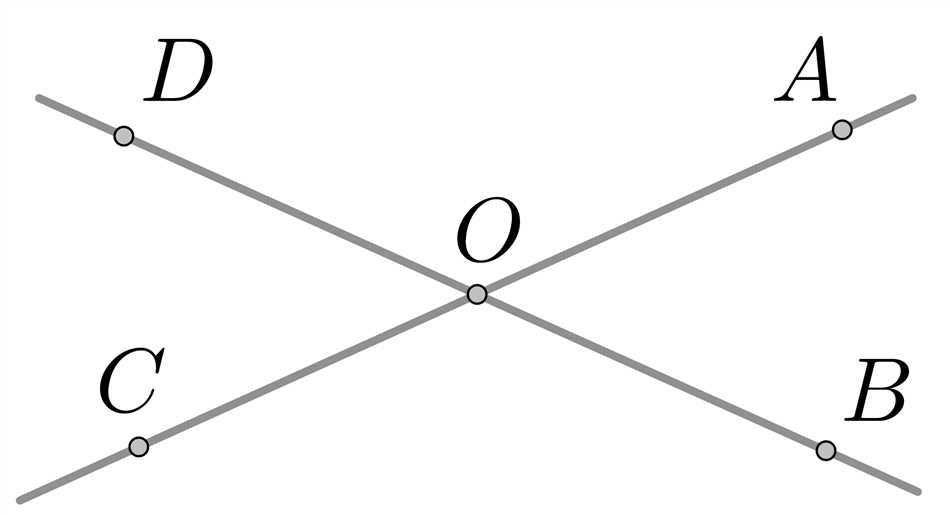
Смежные углы активно используются в различных областях, особенно в геометрии и физике. Например, они могут применяться для измерения угловых скоростей при вращении объектов, в конструировании различных механизмов и систем, а также в архитектуре при проектировании зданий и сооружений.
В математических расчетах смежные углы также играют важную роль. Они позволяют решать задачи на нахождение значения неизвестного угла при известных угловых величинах, а также использовать свойства смежных углов для доказательства различных теорем и утверждений.
Примерами применения смежных углов в повседневной жизни могут служить измерение углов при строительстве и ремонте, а также в навигации для определения направления и ориентации объектов. Кроме того, смежные углы могут использоваться в астрономии для измерения углов созвездий и других небесных объектов.
В итоге, смежные углы являются важным элементом в геометрии и имеют широкие применения в различных областях науки и практики. Понимание и использование свойств смежных углов позволяет улучшить точность измерений, проводить более эффективные расчеты и создавать более устойчивые и функциональные конструкции.