Сочетание — это математический термин, который используется для описания комбинации объектов из заданного множества без учета порядка. В сочетаниях порядок не имеет значения, и каждый объект может использоваться только один раз.
Для понимания понятия сочетания рассмотрим пример: можно рассмотреть сочетание 3 разных цветов из 5 имеющихся цветов: красный, синий, зеленый, желтый и оранжевый. Вот несколько возможных сочетаний:
1) красный, синий, зеленый
2) синий, зеленый, желтый
3) красный, зеленый, желтый
4) оранжевый, синий, зеленый
Здесь порядок цветов не важен, и каждый цвет используется только один раз. Сочетание позволяет описать все возможные комбинации без повторений.
Определение сочетания в математике
Для обозначения сочетаний, используются скобки (), фигурные скобки {} или символ «C». Например, C(5, 2) или {5, 2} или (5, 2) обозначают количество сочетаний из 5 элементов по 2.
Сочетания встречаются в различных ситуациях и задачах, таких как выбор команды из группы игроков, составление меню в ресторане или создание пароля из символов и цифр. Они предоставляют возможность рассчитать количество различных комбинаций, которые можно получить.
Например, если у вас есть 5 различных карточек и вы хотите выбрать 2 из них, то количество сочетаний будет равно 10. Или если у вас есть 3 блюда на выбор в ресторане, и вы хотите выбрать 2 из них, то количество возможных комбинаций будет 3.
Надеюсь, теперь ты понимаешь, что такое сочетание в математике и как его использовать в различных ситуациях.
Простой пример сочетания
Давайте представим, что вы планируете составить команду для участия в викторине. Вам нужно выбрать трех человек из списка десяти друзей. Как вы это сделаете?
Вот где сочетание приходит на помощь! Сочетание — это способ составления комбинаций из определенного количества элементов.
Итак, у вас есть десять друзей, и вы хотите выбрать трех. Сочетание может помочь вам определить количество различных комбинаций, которые вы можете составить из этих друзей. В данном случае, мы используем сочетания без повторений, потому что каждого друга можно выбрать только один раз.
Для того, чтобы посчитать количество сочетаний, мы можем использовать формулу. Для сочетаний без повторений данная формула выглядит так:
C(n, k) = n! / (k!(n-k)!)
Где n — количество элементов в множестве (в данном случае 10 друзей), а k — количество элементов, которые мы выбираем (в данном случае 3).
Таким образом, простым способом решить эту задачу будет использование формулы сочетания: C(10, 3) = 10! / (3! * (10-3)!) = 120, где 10! означает 10 факториал (10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1), и так далее.
Таким образом, существует 120 различных комбинаций, которые вы можете составить из десяти друзей, выбирая трех из них. Теперь вам остается только выбрать свою команду и начать викторину!
Сочетания с повторениями
Допустим, у нас есть множество A={a, b, c}. Мы хотим выбрать 2 элемента из этого множества с учетом повторений. Пусть мы выбрали элемент a дважды. Тогда возможные комбинации будут: aa, ab, ac, bb, bc, cc. Мы видим, что выбранные элементы могут повторяться.
Другой пример — представьте, что вы составляете команду из 5 человек для участия в соревновании. У вас есть 10 кандидатов, и каждый кандидат может быть выбран неограниченное количество раз. В этом случае вам нужно найти количество возможных комбинаций. То есть мы рассматриваем комбинации, где повторения разрешены.
Сочетания с повторениями вы можете рассчитать, используя формулу: C(n+r-1, r), где n — количество элементов в множестве, r — количество выбираемых элементов. Например, в примере с выбором 2 элементов из множества {a, b, c} мы имеем n=3 и r=2, поэтому количество сочетаний с повторениями будет C(3+2-1, 2) = C(4, 2) = 6.
Формула сочетаний
В математике существует удивительный инструмент для подсчета различных комбинаций объектов, называемый формулой сочетаний. Эта формула позволяет решать множество задач и облегчает работу с комбинаторикой.
Формула сочетаний используется, когда нужно выбрать определенное количество элементов из заданного множества. Например, сколько различных команд можно составить из группы 5 человек?
Формула сочетаний выглядит следующим образом: C(n, k) = n! / (k! * (n-k)!), где n — общее количество элементов, k — количество элементов, которые нужно выбрать для комбинации.
Давайте рассмотрим пример: у нас есть 7 различных книг в библиотеке, и мы хотим выбрать 3 книги для чтения. Используя формулу сочетаний, мы получаем следующий результат: C(7, 3) = 7! / (3! * (7-3)!) = 7! / (3! * 4!) = (7*6*5) / (3*2*1) = 35.
Таким образом, у нас есть 35 различных способов выбрать 3 книги из библиотеки.
Формула сочетаний является мощным инструментом для решения задач комбинаторики и может быть применена во многих областях, включая обработку данных, проектирование систем и теорию вероятностей. Применение этой формулы позволяет нам быстро и точно решать задачи, связанные с комбинаторикой, и открывает новые возможности для творческого мышления и анализа.
Количество сочетаний без повторений
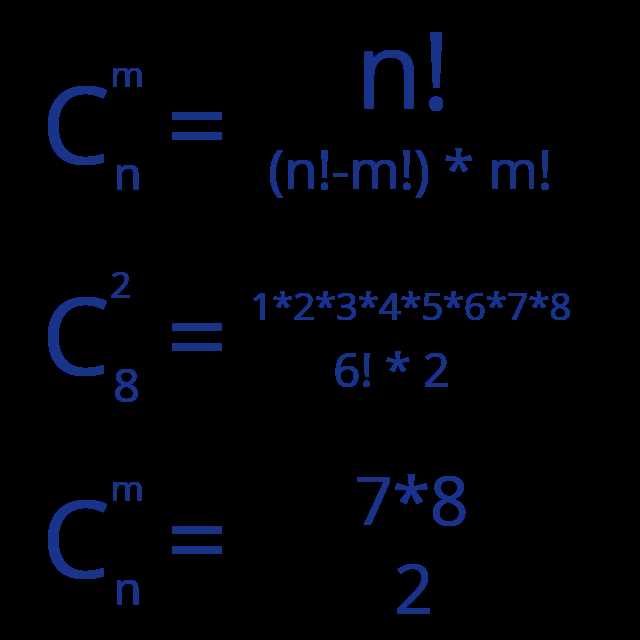
В математике существует такое понятие, как «количество сочетаний без повторений», которое используется для определения количества способов выбрать определенное количество элементов из заданного множества, при этом не учитывая их порядок. Это понятие широко применяется в комбинаторике и теории вероятностей.
Например, предположим, у нас есть 5 разных фруктов: яблоко, груша, апельсин, банан и виноград. Мы хотим выбрать 2 фрукта из этого множества. Для определения количества сочетаний без повторений мы используем следующую формулу:
C(n, k) = n! / (k! * (n — k)!)
- n — количество элементов в множестве (в данном случае фруктов) — в нашем примере это 5
- k — количество элементов, которые мы хотим выбрать (в нашем примере это 2)
- n! — факториал числа n (произведение всех положительных целых чисел от 1 до n)
Таким образом, для нашего примера количество сочетаний без повторений будет:
C(5, 2) = 5! / (2! * (5 — 2)!) = 5! / (2! * 3!) = (5 * 4 * 3!) / (2! * 3!) = 10
Итак, у нас есть 10 разных способов выбрать 2 фрукта из 5-ти.
Важно понимать, что количество сочетаний без повторений зависит от количества элементов в исходном множестве и количества элементов, которые мы хотим выбрать. Изменение любого из этих факторов приведет к изменению количества сочетаний без повторений.
Примеры применения сочетаний в реальной жизни:

- Расчет вероятности: Вероятность — это основной элемент в анализе данных и статистике. При решении задач вероятности, сочетания используются для определения количества возможных исходов или комбинаций, которые могут произойти. Например, при подбрасывании монеты или бросании игральной кости, сочетания позволяют определить количество всех возможных исходов.
- Распределение задач: В реальной жизни мы часто сталкиваемся с необходимостью распределения задач между несколькими людьми или ресурсами. Сочетания помогают нам определить все возможные комбинации распределения задач. Например, в бизнесе сочетания могут использоваться для составления графика работы или для формирования разных групп сотрудников для выполнения различных задач.
- Сочетания в комбинаторике: В комбинаторике сочетания играют важную роль при решении задач на комбинаторные объекты. Одна из простых задач комбинаторики, где сочетания применяются — это задача о распределении различных предметов или людей по группам. Сочетания позволяют нам определить количество различных комбинаций.