Диагонали перпендикулярны — значение и свойства

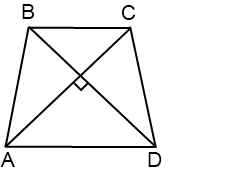
Когда мы говорим о диагоналях, мы обычно представляем себе две линии, которые пересекаются внутри фигуры. Диагональ — это такая линия, которая соединяет две точки, не являющиеся последовательными вершинами фигуры. Итак, что значит, что диагонали перпендикулярны? В этом случае, диагонали образуют перпендикулярные углы между собой. Другими словами, они пересекаются под прямым углом, создавая так называемые прямоугольники. Интуитивно понятно, что такая геометрическая особенность имеет свои применения и может быть полезна для измерения и построения различных объектов.

Раздел 1: Определение перпендикулярности

Перпендикулярность — это одно из самых фундаментальных понятий в геометрии. Давай представим, что у нас есть две линии, и они пересекаются в одной точке под прямым углом. Это означает, что если мы проведем от этой точки перпендикулярные линии к остальным точкам на линиях, то эти линии будут пересекаться под прямыми углами.

Ты можешь представить, насколько это полезно и удивительно? Мы можем использовать перпендикулярность, чтобы строить прямые, измерять расстояния или определять строительные углы. Она помогает нам создавать структуры, архитектуру и даже решать задачи в математике.

Но как мы можем узнать, что линии действительно перпендикулярны? Существует несколько способов, но один из самых простых — это использовать угломер или гониометр. Возьми угломер и измерь угол между двумя линиями. Если угол равен 90 градусам, значит, линии перпендикулярны.

Теперь, когда ты знаешь, что такое перпендикулярность, можешь ли ты представить, где еще она может пригодиться в нашей жизни? Как мы можем использовать ее в повседневных ситуациях?

• Можно использовать перпендикулярность для укладки плитки на поле или стене. Если линии перпендикулярны, то плитка будет идеально ровной и симметричной.
• Перпендикулярность помогает нам при парковке автомобиля. Когда мы паркуемся рядом с другим автомобилем, мы можем использовать геометрию, чтобы максимально использовать пространство.
• Если у нас есть велосипед, то мы можем использовать перпендикулярность для настройки передних и задних тормозов. Это поможет нам и безопасно ездить.

Так что перпендикулярность не только полезна и интересна, она также применима во многих сферах нашей жизни. Не забывай об этом и используй этот замечательный инструмент, чтобы решать задачи и строить что-то новое!

Понятие перпендикулярности

Ты знаешь, перпендикулярные отношения – это нечто уникальное и магическое. Как правило, важно, чтобы одна прямая была вертикальной, а другая – горизонтальной. Именно благодаря этому, они создают баланс и гармонию. И это превращает их в прекрасную связь, где каждый объект дополняет и усиливает другой. Думаю, это как духовное и эмоциональное переплетение, где две линии никогда не сталкиваются или пересекаются, они просто живут бок о бок, придавая взаимному существованию более глубокий смысл.

Свойства перпендикулярных прямых

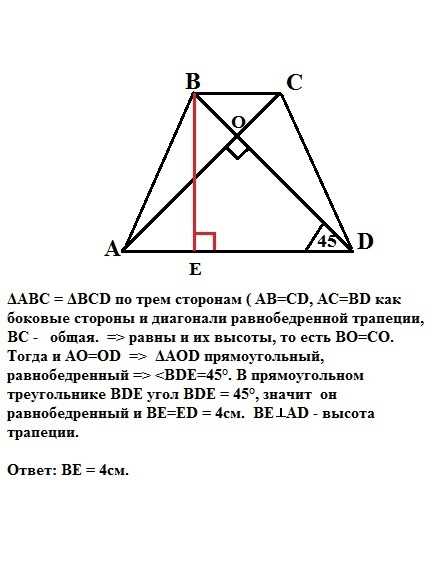
Что значит, когда говорят, что диагонали перпендикулярны? Это означает, что они пересекаются под прямым углом. Но какие еще свойства у перпендикулярных прямых? Давайте разберемся!

Первое свойство — перпендикулярные прямые имеют равные градусные меры своих углов. Это значит, что два угла, образованные пересечением перпендикулярных прямых, будут равными и равными 90 градусам. Это свойство позволяет нам использовать перпендикулярные прямые при решении геометрических задач, таких как нахождение высоты параллелограмма или построение перпендикуляра к заданной прямой.

Второе свойство перпендикулярных прямых состоит в том, что они не пересекаются нигде, кроме точки их пересечения. Если бы перпендикулярные прямые имели еще одну точку пересечения, они были бы параллельными, а не перпендикулярными. Это свойство делает перпендикулярные прямые очень уникальными и помогает нам определять их в геометрических фигурах.

Третье свойство — перпендикулярные прямые образуют квадратные углы. Квадратный угол равен 90 градусам, и он является самым большим углом, который можно сформировать на плоскости. Когда перпендикулярные прямые пересекаются, они образуют четыре квадратных угла, которые в сумме дают 360 градусов. Это свойство позволяет нам работать с перпендикулярными прямыми в различных контекстах, например, при решении уравнений с использованием перпендикулярных граней, законов сопротивления или при проектировании зданий.

В заключении, перпендикулярные прямые имеют множество свойств, которые делают их важными в геометрии и на практике. Зная эти свойства, мы можем легко работать с перпендикулярными прямыми и использовать их в различных ситуациях. И помните, перпендикулярные прямые всегда пересекаются под прямым углом!

Раздел 2: Диагонали в геометрии

Представь себе четырехугольник, например, квадрат. В нем есть две диагонали — одна соединяет вершины, расположенные на одной горизонтальной стороне, а другая — на одной вертикальной стороне. Если эти две диагонали пересекаются и образуют прямой угол, то можно сказать, что диагонали перпендикулярны.

Концепция перпендикулярных диагоналей имеет применение в различных областях геометрии. Например, в треугольниках, перпендикулярные диагонали могут быть использованы для нахождения высот, медиан и биссектрис. В прямоугольниках и ромбах, перпендикулярные диагонали помогают определить центр фигуры и рассчитать площадь.

Знание того, что диагонали перпендикулярны, может быть полезным в различных ситуациях. Например, при построении зданий или расположении мебели, где точность и симметрия играют важную роль.

Определение диагонали

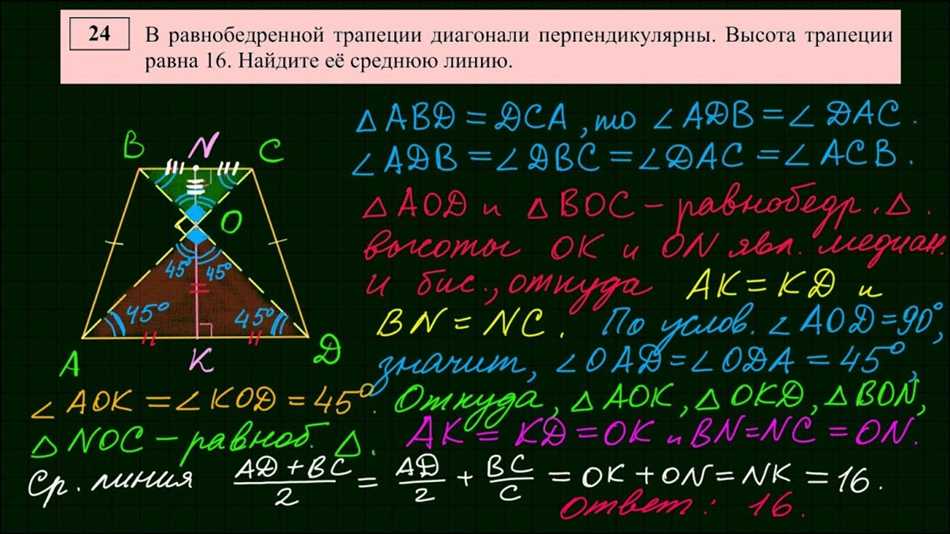
Диагональ – это отрезок, который соединяет две вершины многоугольника и не принадлежит его сторонам. Мы часто сталкиваемся с примерами диагоналей в повседневной жизни. Например, представь планету Земля: линия, которая соединяет две противоположные точки на поверхности Земли – это диагональ. Другим примером может быть прямоугольник: его диагонали соединяют противоположные углы.

Диагонали играют важную роль в геометрии. Например, для квадрата или ромба диагонали равны между собой, а для прямоугольника они не равны, но пересекаются по середине. А ты можешь предложить еще примеры фигур с диагоналями? Расскажи, где еще можем их встретить в повседневной жизни!

Свойства диагоналей

Первое свойство диагоналей — они могут быть равными или неравными. Равные диагонали обычно встречаются в симметричных фигурах, например, в прямоугольниках и квадратах. В этих фигурах, диагонали делятся пополам и их длины равны.

Второе свойство диагоналей — они могут быть перпендикулярными или неперпендикулярными. Диагонали прямоугольников всегда перпендикулярны, это одно из определений прямоугольника. А в случае параллелограмма, диагонали могут быть неперпендикулярными. Они образуют углы между собой, и, кстати, эти углы равны.

И последнее свойство, о котором я хочу сказать — диагонали могут быть осью симметрии. Ось симметрии — это такая линия, которая делит фигуру на две равные части. Диагонали ромба и параллелограмма могут быть осями симметрии.

Прекрасно, что диагонали могут быть такими разными, ведь они создают интересные свойства фигур. Теперь, когда ты знаешь о них, можно увидеть диагонали везде вокруг — в окнах домов, на полях шахматной доски или даже в карточных играх! Вопреки мнению некоторых, геометрия не такая скучная наука, как может показаться. Она полна удивительных открытий и магии форм. Представь, как много диагоналей скрыто в мире!

Раздел 3: Понятие перпендикулярных диагоналей

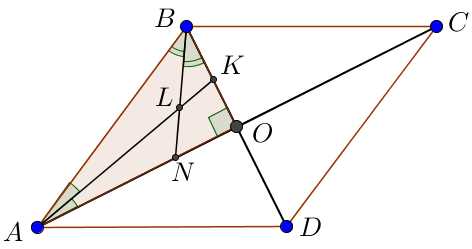
То есть, перпендикулярные диагонали — это когда линия, проходящая от одной вершины прямоугольника к противоположной вершине, пересекает линию, проходящую от другой вершины к еще одной противоположной вершине, и эти две линии пересекаются под прямым углом. Восхитительно, не правда ли? Когда диагонали перпендикулярны, они создают два треугольника — это прекрасный способ представления геометрических фигур.

Раздел 4: Определение перпендикулярности диагоналей

Давай-ка я расскажу тебе о том, что значит, когда говорят, что диагонали перпендикулярны. Это довольно простое понятие, которое имеет большое значение в геометрии.

Перпендикулярность диагоналей означает, что две линии, проведенные от противоположных углов в прямоугольнике, пересекаются в прямом угле. Другими словами, они образуют 90-градусный угол, который никак нельзя назвать неправильным.

Это может показаться несколько абстрактным, но если посмотреть на прямоугольник, становится ясно: диагонали прямоугольника пересекаются под прямым углом. Воображение включается, и ты начинаешь видеть, как все вписывается.

Это очень полезное свойство диагоналей, которые перпендикулярны. Оно помогает нам решать различные геометрические задачи и дает нам понимание форм и пропорций.

Так что, теперь ты знаешь, что значит, когда говорят, что диагонали перпендикулярны. Это означает, что они пересекаются под прямым углом. Не забывай об этом, когда будешь решать геометрические задачи!