Интервалы играют важную роль в алгебре 7 класса и помогают нам лучше понять множество чисел. Что такое интервал? Интервал — это непрерывный участок числовой прямой между двумя значениями. Он может быть ограничен или неограничен, а также может включать или не включать границы.
Интервалы могут быть представлены в виде знаковых или числовых неравенств. Например, интервал [3, 7] включает числа от 3 до 7 включительно, в то время как интервал (1, 5) содержит числа от 1 до 5, но исключает границы.
Основные свойства интервалов помогают нам определить их принадлежность к другим интервалам, а также сравнить их длину. Использование интервалов в алгебре позволяет решать различные уравнения и неравенства, а также применять их в задачах о времени, расстоянии и других величинах.
Определение интервала
Чтобы понять это понятие лучше, представим себе множество чисел на числовой прямой. Интервал будет выделять некоторую часть этого множества. Например, интервал от 1 до 5 включает числа 1, 2, 3, 4 и 5.
Ограниченный интервал имеет начало и конец, которые обозначаются точками на числовой прямой. Например, интервал от 1 до 5 будет обозначаться как (1, 5). Здесь 1 и 5 включены в интервал и обозначают его границы. Неограниченный интервал не имеет конкретного начала или конца и обозначается соответствующим знаком бесконечности. Например, интервал от 3 до бесконечности будет обозначаться как (3, ∞).
Интервалы могут быть открытыми, когда границы не входят в интервал, и закрытыми, когда границы входят в интервал. Например, интервал от 1 до 5 может быть открытым (1, 5), когда 1 и 5 не включены, или закрытым [1, 5], когда 1 и 5 включены.
Виды интервалов
Следующий вид интервала — закрытый интервал. Он обозначается квадратными скобками и содержит все числа, которые находятся между двумя конкретными значениями, включая сами эти значения. Например, [2, 5] — это интервал, включающий все числа, которые больше или равны 2 и меньше или равны 5.
Также существует полуоткрытый интервал, который содержит либо левую границу, либо правую границу, но не обе. Левый полуоткрытый интервал обозначается квадратной скобкой с включением левой границы, а правый полуоткрытый — круглой скобкой со включением правой границы. Например, [2, 5) — это интервал, включающий 2 и все числа, которые больше 2 и меньше 5, а (2, 5] — это интервал, включающий 5 и все числа, которые больше 2 и меньше или равны 5.
И, наконец, бесконечные интервалы. Они представляют собой интервалы, которые не имеют конечных значений. Бесконечный интервал может быть открытым или закрытым. Например, (-∞, 5) — это открытый интервал, содержащий все числа, которые меньше 5, а (-∞, ∞) — это открытый интервал, содержащий все числа.
Бесконечные интервалы
А ты когда-нибудь задумывался о том, что интервалы могут быть не только ограниченными, но и бесконечными? Нет? Тогда держись, сейчас все выясним!
Так вот, бесконечные интервалы – это интервалы, которые не имеют конца или начала. Возможно, ты уже слышал о «интервалах (a; +∞)» или «интервалах (-∞; b)». Как тебе такое? Бесконечность – непривычная штука, не правда ли?
Самое интересное в том, что мы можем объединить ограниченные и бесконечные интервалы в одно понятие – рациональные числа. Подумай о том, что будет, если мы возьмем все рациональные числа от 0 до +∞. Получится бесконечный интервал (0; +∞), в котором каждое число расположено на своем промежутке и не имеет конкретного значения.
Так что, как тебе такая возможность – бесконечные интервалы? Не забывай, что математика – это череда открытий и вопросов без конца. И пока мы не нашли все ответы, давай наслаждаться исследованием этого увлекательного предмета!
Отрезок и полуинтервал
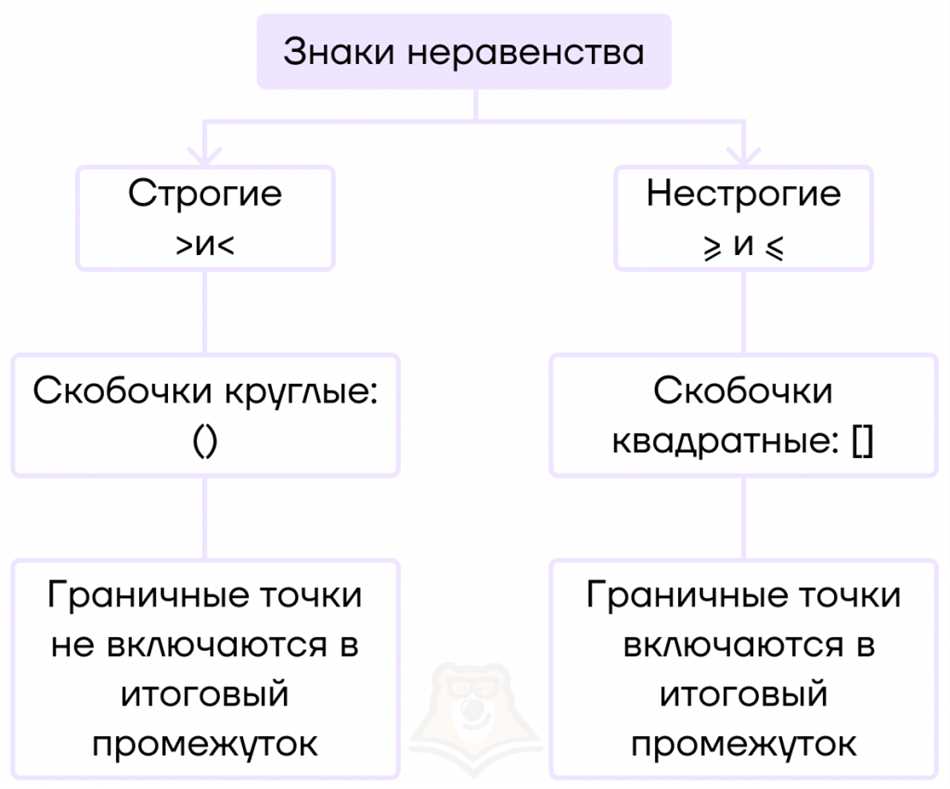
Начнем с отрезка. В математике отрезок — это промежуток между двумя точками на числовой прямой. Он обозначается двумя точками в скобках, например, [a, b]. Тут a — левая граница отрезка, а b — правая граница. Заметь, что обе эти точки принадлежат отрезку.
Исходя из определения отрезка, понятие полуинтервала становится более понятным. Полуинтервал — это часть отрезка, которая расположена между двумя точками, но не включает их. В зависимости от того, включаем мы левую границу или правую, полуинтервалы бывают левооткрытые, правооткрытые или открытые. Например, (a, b) — правооткрытый полуинтервал, так как включает в себя все значения от a до b, кроме самой b.
Зачем нам знать эти понятия? Они полезны при изучении множеств и отрезков на числовой прямой. В алгебре мы часто работаем с различными промежутками для определения областей допустимых значений переменных и решения уравнений или неравенств. Кроме того, отрезки и полуинтервалы помогают нам лучше понимать свойства и операции на числовой оси.
Итак, отрезок и полуинтервал — это инструменты, которые помогают нам лучше понять и работать с числовой прямой. Постарайся применить эти понятия в своих заданиях и увидишь, как они облегчат твою работу и помогут понять математику еще лучше. Удачи!
Промежутки

В алгебре мы часто сталкиваемся с понятием промежутков. Но что это такое? Давайте разберемся.
Промежуток — это некоторый интервал на числовой прямой. Это может быть отрезок между двумя числами или неограниченный интервал. Например, промежуток от 1 до 5 включает числа 1, 2, 3, 4 и 5. А неограниченный промежуток от 2 до бесконечности включает все числа, большие или равные 2.
Когда мы работаем с промежутками, нам часто нужно знать их основные свойства. Например, если имеется два промежутка, то их пересечение — это такой промежуток, который содержит только те числа, которые принадлежат обоим исходным промежуткам. А объединение промежутков — это промежуток, который содержит все числа из обоих исходных промежутков.
Промежутки могут нам помочь в решении различных задач. Например, если нам дано условие, что x принадлежит определенному промежутку, мы можем использовать это условие для нахождения значения x, которое удовлетворяет этому промежутку.
Так что не бойтесь промежутков! Используйте их в своих алгебраических задачах и они помогут вам найти правильные решения. Ведь понимание промежутков — это важный инструмент в алгебре.
Свойства интервалов
Одно из основных свойств интервалов – это их включение или исключение точек на концах. Например, интервал (2, 5) не включает точки 2 и 5, а интервал [2, 5] включает их. Подобная разница имеет большое значение в решении различных задач, поэтому внимательность очень важна.
Обрати внимание на то, что интервал может быть неограниченным. Например, интервал [2, +∞) означает, что все числа, начиная с 2, входят в этот интервал, а интервал (-∞, 5) означает, что все числа, меньше 5, входят в этот интервал.
Интервалы могут также сочетаться в математических операциях. Например, при суммировании и вычитании интервалов, результатом будет интервал, который включает все числа, находящиеся между двумя исходными интервалами. Запомни это правило: операции с интервалами ведут себя подобно операциям с числами.
Свойства интервалов играют большую роль в алгебре и математике в целом. Они помогают нам более точно и гибко работать с числами и решать различные задачи.
Операции с интервалами
Интервалы в алгебре играют важную роль при решении различных задач. Они представляют собой некоторое множество чисел, которые удовлетворяют определенным условиям. Однако, для работы с интервалами необходимо знать основные операции, которые можно выполнять над ними. В этой статье мы рассмотрим основные операции с интервалами.
Объединение интервалов – это операция по объединению двух или более интервалов в один. При объединении интервалов, получается новый интервал, который включает в себя все числа, принадлежащие каждому из исходных интервалов.
Пересечение интервалов – это операция, которая определяет все числа, которые одновременно принадлежат двум или более интервалам. Пересечение может быть пустым множеством, если у интервалов нет общих чисел.
Разность интервалов – это операция, при которой из одного интервала вычитается другой интервал. Результатом операции является новый интервал, который содержит числа, принадлежащие только первому интервалу и не принадлежащие второму.
Операции с интервалами позволяют совершать различные манипуляции с числами и упрощать вычисления в алгебре. Основные операции – объединение, пересечение и разность – позволяют находить новые интервалы и определять их свойства. Грамотное использование операций с интервалами поможет эффективно решать задачи и углублять понимание алгебры.