Исследование на монотонность является важным инструментом для анализа данных и определения трендов и изменений в определенной области. Оно используется в различных областях, включая экономику, статистику и биологию.
Основное понятие, связанное с исследованием на монотонность, — это монотонная функция. Монотонная функция — это функция, которая либо всегда возрастает, либо всегда убывает, без повторений значений. Исследование на монотонность заключается в определении, сохраняется ли упорядоченность данных во времени или пространстве.
Существует несколько подходов к исследованию на монотонность, включая использование графиков и статистических методов. Графики позволяют визуально оценить поведение данных и определить, является ли функция монотонной. Статистические методы, такие как ранговая корреляция и регрессионный анализ, помогают оценить степень монотонности в данных.
Исследование на монотонность имеет широкий спектр применения и позволяет лучше понимать закономерности в данных. Это мощный инструмент, который помогает выявить тренды и изменения в динамике информации и принимать обоснованные решения на основе анализа этих изменений.
Основные понятия и подходы в исследовании на монотонность
Значение понятия «монотонность» может быть разным в разных областях знаний, но в контексте математики исследование на монотонность связано с анализом функций и их поведения.
В основе исследования на монотонность лежит понятие производной функции. Производная функции показывает, как быстро функция меняется в каждой точке. Если производная положительна на всем промежутке, то функция монотонно возрастает. Если производная отрицательна на всем промежутке, то функция монотонно убывает. Если производная равна нулю в точке, то это может быть экстремум функции.
Для исследования на монотонность функции можно использовать различные подходы, например, графический или алгебраический. Графический подход основан на построении графика функции и анализе его формы и направления. Алгебраический подход связан с вычислением производных функции и анализом их знаков на заданном промежутке.
Важным аспектом исследования на монотонность является также определение интервалов, на которых функция монотонна. Для этого нужно анализировать случаи, когда производная меняет знак и определять, где функция возрастает или убывает.
Исследование на монотонность функций позволяет лучше понять их свойства и поведение. Это важный инструмент в математике и имеет широкий спектр применения, включая оптимизацию, построение графиков функций и нахождение экстремальных значений.
Что такое монотонность и почему она важна?
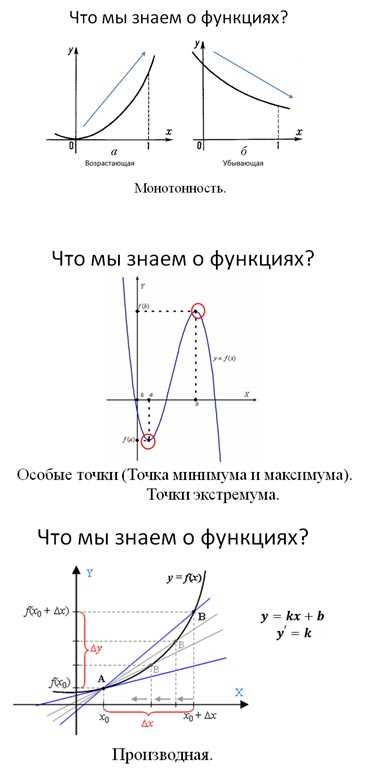
Ну, подумайте, вы хотите анализировать поведение функции, как она меняется в зависимости от изменения ее аргумента, верно? А монотонность – ключевой индикатор того, как функция меняется со временем. Исследуя монотонность функции, мы можем понять, где она возрастает, где убывает, и где достигает экстремумов.
Ну хорошо, но почему монотонность так важна? Это позволяет нам упростить анализ функций. Например, монотонность помогает нам определить, где функция достигает своих минимальных и максимальных значений. Заранее зная, что функция монотонно возрастает, мы можем сразу сказать, что минимум будет достигаться в начале графика, и наоборот, если она монотонно убывает, то максимум будет достигаться в начале графика. Это весьма полезная информация при анализе функций.
Так что помните, монотонность – это хорошая штука. Познакомьтесь с ней поближе, и она поможет вам разобраться во многих задачах и анализировать функции с большей легкостью.
Способы обнаружения монотонности в данных
Один из способов обнаружения монотонности — визуальный анализ графика. Если график данных имеет явно возрастающий или убывающий тренд, то можно предположить, что данные монотонны. Однако, такой подход может оказаться недостаточно точным или может привести к ошибкам — особенно при работе с большими объемами данных.
Более точный способ — использование статистических методов. Например, можно применить статистический тест на монотонность, такой как тест Манна-Кендалла или тест Спирмена. Эти тесты позволяют оценить статистическую значимость и направление монотонности данных.
Еще один подход — применение алгоритмов машинного обучения. Некоторые модели, такие как решающие деревья или логистическая регрессия, могут автоматически определять монотонность данных и использовать ее при предсказаниях.
В конечном счете, выбор способа обнаружения монотонности зависит от конкретной задачи и доступных данных. Иногда может понадобиться комбинировать несколько подходов или проводить дополнительные исследования для уверенности в результате. Важно помнить, что обнаружение монотонности — это лишь первый шаг, и дальнейший анализ и интерпретация данных может потребовать дополнительных усилий и знаний.
Анализ монотонности в статистике и экономике
В статистике монотонность может быть использована, чтобы определить направление тренда в данных. Например, если у нас есть временной ряд, показывающий изменение цен на товары в течение нескольких месяцев, мы можем провести анализ монотонности и узнать, растет ли или падает средняя цена товара. Это может быть полезной информацией для бизнеса, позволяющей прогнозировать будущие изменения и принимать соответствующие решения.
В экономике анализ монотонности может помочь нам понять взаимосвязь между двумя переменными. Например, если у нас есть данные о расходах на рекламу и продажах продукта, мы можем провести анализ, чтобы увидеть, как изменение расходов влияет на изменение продаж. Если мы обнаружим положительную монотонность, то это будет означать, что увеличение расходов на рекламу приводит к росту продаж.
Анализ монотонности позволяет нам использовать математический подход для изучения данных и выявления важных моментов в поведении переменных. Это мощный инструмент, который помогает нам принимать более информированные решения в бизнесе и экономике. Понимание монотонности помогает нам видеть суть происходящего и прогнозировать будущие тренды и изменения.
Исследование на монотонность в машинном обучении
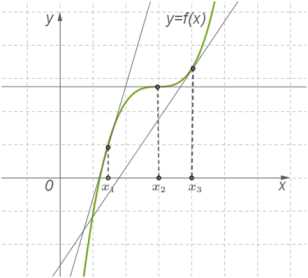
Когда мы исследуем монотонность, мы стремимся выявить закономерности в данных и определить, как одна переменная изменяется в зависимости от другой. Например, мы можем исследовать, как рост температуры влияет на количество продаж некоторого товара. Если мы обнаружим, что с ростом температуры количество продаж также растет, то мы можем заключить, что здесь присутствует положительная монотонность.
Итак, как мы исследуем монотонность в машинном обучении?
Существуют различные подходы к исследованию монотонности в машинном обучении, и один из них — это использование графического анализа. Мы можем построить график зависимости двух переменных и визуально оценить, является ли эта зависимость монотонной. Если график демонстрирует однозначное возрастание или убывание, то мы можем говорить о монотонной связи.
Второй подход — это использование статистических методов, таких как корреляция и моделирование. Мы можем рассчитать коэффициент корреляции между двумя переменными, чтобы определить, насколько они связаны между собой. Если корреляция близка к 1 или -1, то это указывает на сильную монотонную связь. Мы также можем построить модель, учитывая монотонную связь, и оценить ее точность и предсказательную способность.
- Кроме того, исследование на монотонность может быть полезно для отбора признаков в моделях машинного обучения. Если мы знаем, что некоторые признаки обладают монотонной связью с целевой переменной, то мы можем использовать только эти признаки, чтобы улучшить производительность модели. Это позволяет упростить модель и сократить вычислительные затраты.
- Исследование на монотонность также актуально в задачах прогнозирования и оптимизации. Понимание направления и силы взаимосвязи между переменными позволяет нам принимать более осмысленные и информированные решения. Мы можем использовать эту информацию для оптимизации бизнес-процессов, улучшения производительности и повышения эффективности.
Методы для проверки монотонности функций
Существует несколько методов для проверки монотонности функций. Один из самых простых способов — это рассмотреть производную функции. Если производная положительна на всей области определения функции, то она монотонно возрастает. Если производная отрицательна, то функция монотонно убывает.
Производная функции показывает нам, как функция меняется в зависимости от значения аргумента. Она вычисляется путем нахождения предела разности значений функции в двух точках и разности аргументов этих точек, когда эти точки стремятся к нулю. Если производная функции положительна, это означает, что функция увеличивается со временем. Если она отрицательна, это означает, что функция убывает.
Однако, следует помнить, что существуют и другие методы для проверки монотонности функций, такие как метод исследования функций на интервале изменения аргумента, анализ таблицы знаков и другие. Каждый из этих методов имеет свои особенности и подходы, и выбор подходящего метода будет зависеть от конкретной задачи и функции, с которой мы работаем.
Заключение
В данной статье мы рассмотрели основные понятия и подходы к исследованию на монотонность.
Исследование на монотонность является важным инструментом в математике и других науках, так как позволяет определить поведение функции на заданном интервале. Монотонность функции может быть возрастающей, убывающей или постоянной, а также может быть локальной или глобальной.
Примеры применения исследования на монотонность включают определение экстремумов функции, поиск интервалов возрастания или убывания функции, определение областей значений функции и построение графиков. Также исследование на монотонность может использоваться для решения оптимизационных задач и определения стабильности систем в физике и экономике.