Как обозначаются многоугольники?

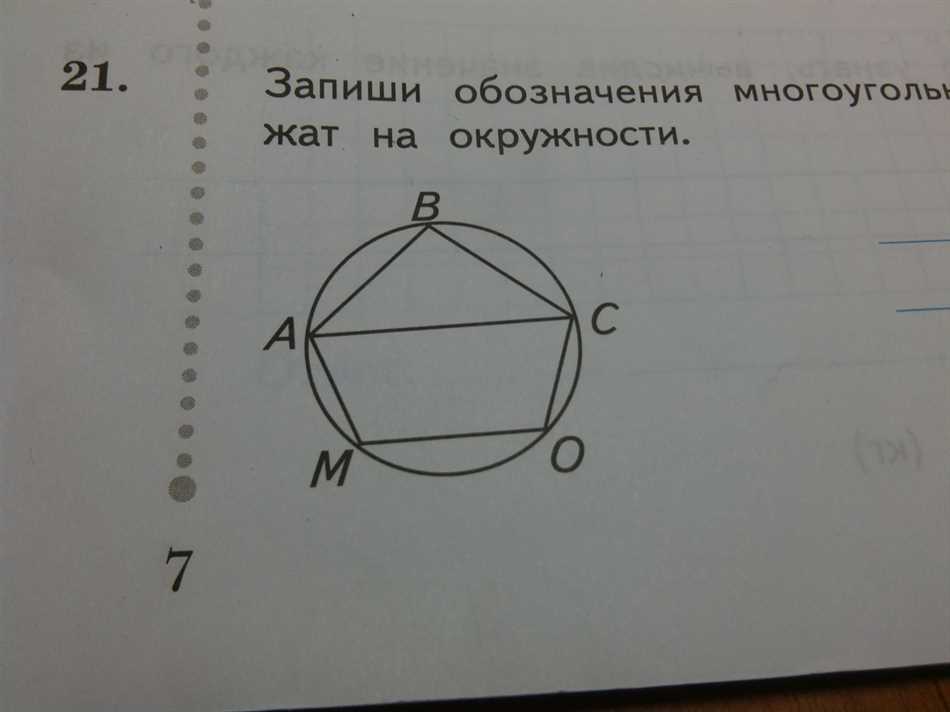
Когда мы говорим о многоугольниках, мы обычно имеем в виду геометрические фигуры со множеством углов и сторон. Обозначение многоугольника может быть важным аспектом в изучении геометрии. Чтобы определить многоугольник, есть несколько способов его обозначить. Например, можно использовать буквы для обозначения каждого угла и каждой стороны. Также многоугольник можно обозначить по количеству его углов и сторон, например, треугольник — это многоугольник с тремя углами и тремя сторонами. Обозначение многоугольника играет важную роль в геометрии, помогая нам лучше понять его свойства и характеристики.

Абстрактное представление многоугольников

В абстрактном представлении многоугольники обычно определяются по числу их сторон и углов. Например, треугольник — это многоугольник с тремя сторонами и тремя углами, у четырёхугольника — четыре стороны и четыре угла, и так далее. Каждый многоугольник имеет своё уникальное имя — треугольник, прямоугольник, пятиугольник, шестиугольник и так далее.

Абстрактное представление многоугольников используется, чтобы упростить изучение и анализ геометрических фигур. С помощью абстрактного подхода можно выявить общие свойства и закономерности, которые присущи всем многоугольникам независимо от их конкретной формы или размера. Например, все многоугольники имеют сумму внутренних углов, равную 180 градусов, или теорему Пифагора применимы к прямоугольным треугольникам.

Кроме того, абстрактное представление многоугольников позволяет изучать их свойства и взаимодействие друг с другом в различных математических и геометрических моделях. Например, всякая выпуклая комбинация многоугольников будет являться новым многоугольником, и можно определить отношение площадей многоугольников или их периметров.

Определение

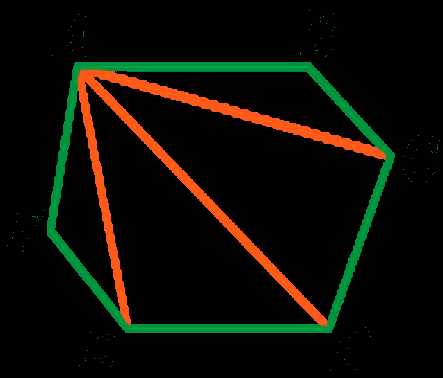
Многоугольники могут быть разных форм и размеров, включая треугольники, четырехугольники, пятиугольники и так далее. Каждый многоугольник имеет определенную структуру, которая определяет количество сторон, их длины и углы между ними. Например, треугольник имеет три стороны и три угла, а четырехугольник имеет четыре стороны и четыре угла.

Основные параметры многоугольника включают длины сторон, углы между сторонами и координаты вершин. Для определения многоугольника, обычно указывают либо длины всех его сторон, либо координаты всех его вершин. Например, треугольник можно определить, указав длины всех его сторон или координаты его трех вершин.

Многоугольники широко используются в различных областях науки и практических приложений. Например, они используются в геодезии для измерения земельных участков, в архитектуре для построения зданий, в компьютерной графике для создания 2D и 3D моделей, а также в играх для задания формы объектов и коллизий между ними.

Таким образом, определение многоугольника состоит в понимании его структуры и параметров, таких как количество сторон, их длины и углы между ними. Это базовая концепция геометрии, которая находит широкое применение в различных областях, предоставляя нам понимание и инструменты для изучения и работы с фигурами в двумерном пространстве.

Основные характеристики многоугольников

Основными характеристиками многоугольников являются:

1. Количество сторон: Многоугольники могут иметь любое количество сторон, начиная от трех и более. Например, треугольник — многоугольник с тремя сторонами, четырехугольник — многоугольник с четырьмя сторонами и так далее.
2. Количество углов: Количество углов в многоугольнике равно количеству его сторон. Например, треугольник имеет три угла, четырехугольник — четыре угла и так далее.
3. Типы углов: В многоугольниках могут быть разные типы углов. Например, прямоугольник имеет все углы прямые (равны 90 градусам), равносторонний треугольник имеет все углы равные (равны 60 градусам).
4. Типы сторон: В многоугольниках могут быть разные типы сторон. Например, равносторонний треугольник имеет все стороны равными, равнобедренный треугольник имеет две стороны равными.
5. Периметр: Периметр многоугольника — это сумма длин всех его сторон. Он используется для измерения длины фигуры и определения ее размеров.
6. Площадь: Площадь многоугольника — это пространство, заключенное внутри его контура. Ее можно вычислить разными способами в зависимости от формы многоугольника.

Знание основных характеристик многоугольников помогает в изучении и понимании их свойств и использовании их в различных областях, таких как геометрия, архитектура, дизайн и других.

Классификация многоугольников

Давайте рассмотрим несколько основных классификаций многоугольников и рассмотрим их характеристики:

По количеству сторон:

• Треугольник – многоугольник с тремя сторонами. Треугольники можно назвать самыми простыми и распространенными многоугольниками. Они могут быть равносторонними (все стороны равны), равнобедренными (две стороны равны) или разносторонними (все стороны разные).
• Четырехугольник – многоугольник с четырьмя сторонами. Четырехугольники могут быть прямоугольными (имеют прямые углы) или непрямоугольными (все углы не прямые).
• Пятиугольник – многоугольник с пятью сторонами. Пятиугольники могут иметь разные формы и размеры.
• Шестиугольник – многоугольник с шестью сторонами. Шестиугольники также могут иметь различные формы и размеры.
• Многоугольник с более чем шестью сторонами – для многоугольников с более чем шестью сторонами мы просто указываем количество сторон. Например, семиугольник, восьмиугольник и так далее.

По форме:

• Равносторонний – многоугольник, у которого все стороны равны.
• Равнобедренный – многоугольник, у которого две стороны равны.
• Разносторонний – многоугольник, у которого все стороны разные.

По углам:

• Прямоугольник – многоугольник, у которого все углы прямые (90 градусов).
• Остроугольный – многоугольник, у которого все углы острые (меньше 90 градусов).
• Тупоугольный – многоугольник, у которого есть углы, превышающие 90 градусов.

Таким образом, многоугольники могут быть различных типов в зависимости от количества сторон, формы и углов. Изучение и классификация многоугольников помогает нам лучше понять их свойства и особенности, а также применять эти знания в различных сферах науки и практики.

Способы обозначения многоугольников

Многоугольники используются в различных математических задачах и решениях. Они также широко применяются в архитектуре, дизайне, графике и других областях. При работе с многоугольниками необходимо иметь возможность идентифицировать их и отличать друг от друга.

Существуют различные способы обозначения многоугольников:

• Буквенное обозначение: Многоугольники могут быть обозначены буквами латинского алфавита, например, A, B, C и т.д. Это позволяет легко идентифицировать каждую фигуру и использовать их в дальнейших вычислениях.
• Конечные точки: Многоугольники могут быть обозначены по координатам своих вершин. Например, треугольник ABC можно обозначить как (A,B,C), где A, B и C — это координаты точек на плоскости.
• Углы: Многоугольники можно обозначить с использованием углов между их сторонами. Например, треугольник ABC можно обозначить как ∠ABC, ∠BCA и т.д., где ∠ — обозначение угла.
• Таблицы: Многоугольники могут быть представлены в виде таблицы, где каждая строка соответствует одной вершине, а столбцы содержат координаты этой вершины.

Выбор способа обозначения многоугольников зависит от ситуации и предпочтений человека. Важно только, чтобы обозначение было понятным и удобным для осуществления необходимых вычислений или анализа геометрических свойств.

Используйте эти способы обозначения, чтобы упростить свою работу с многоугольниками и больше не запутываться в их идентификации!

Обозначение многоугольника

В математике многоугольник обозначается с помощью прописных латинских букв, обычно заглавных. Количество сторон многоугольника указывается нижним индексом после обозначения. Например, для треугольника используется обозначение АВС₃.

Многоугольники могут быть различной формы и иметь разное количество сторон. Существуют следующие обозначения для некоторых типов многоугольников:

• Треугольник — АВС₃
• Четырехугольник — АВСD₄
• Пятиугольник — АВСDE₅
• Шестиугольник — АВСDEF₆
• Семиугольник — АВСDEFG₇

Таким образом, многоугольник просто обозначается прописной латинской буквой, а его количество сторон указывается нижним индексом после обозначения.