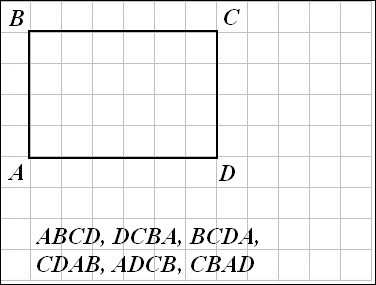
Когда мы говорим о прямоугольнике, то часто используем специальное обозначение, которое помогает нам лучше понять его форму и размеры. Прямоугольник обычно обозначается с помощью двух перпендикулярных линий и четырех углов. Горизонтальная линия называется основанием прямоугольника, а вертикальная — высотой. Углы прямоугольника обозначаются буквами A, B, C и D, а стороны — a, b, c и d. Это обозначение позволяет нам легко обращаться с прямоугольниками и решать задачи, связанные с их геометрией.
Исторический контекст
Давайте сматериализуемся во времени и вместе отправимся в первую половину XIX века. В это время мир меняется, преображается, и наступает эпоха промышленной революции. Везде пылает огонь развития, и люди с нетерпением смотрят вперед, открывая новые возможности и горизонты.
Именно в этот период и возникает необходимость в создании системы стандартных обозначений для геометрических фигур, включая прямоугольник. Растущая потребность в точности и единстве в измерениях привела к тому, что ученые и инженеры начали активно работать над разработкой универсальных символов и обозначений для различных геометрических фигур.
Сначала были созданы базовые символы, которые впоследствии развились в систему, принятую в наше время. Сотни ученых, математиков и инженеров внесли свой вклад в формирование этой системы, и их труды сформировали основу для современных обозначений геометрических фигур, включая прямоугольник.
Если мы посмотрим на историю и развитие обозначений прямоугольника, то мы обязательно увидим, что эти символы и формы не возникли из ниоткуда. Они стали результатом тщательной работы многих поколений ученых и математиков, которые стремились создать универсальную систему обозначений для геометрических фигур.
И таким образом, исторический контекст обозначения прямоугольника свидетельствует о богатстве нашего знания истории и развития геометрии. Это результат коллективного труда многих ученых и инженеров, которые стремились сделать наш мир лучше и более точным.
Происхождение названия
Слово «прямоугольник» образовано от двух корней: «прямой» и «угол». Но что значит каждое из этих слов? «Прямой» означает, что все углы внутри фигуры равны 90 градусам. «Угол» – это место, где две прямые линии встречаются и образуют острый или тупой угол. Таким образом, «прямоугольник» можно перевести как «фигура с прямыми углами».
Видимо, люди давно заметили, что фигуры с прямыми углами имеют особую форму и решили называть их «прямоугольниками». Ведь они выглядят именно так – как прямые линии, встречающиеся под прямыми углами.
Но для того, чтобы придумать это название, нужно было провести много наблюдений и анализа. Ведь в природе не так много прямоугольных фигур. На самом деле, прямоугольник – это абстрактное понятие, связанное с геометрией и математикой.
Интересно помирить прямые линии и геометрию с реальным миром. Может быть, ты уже замечал прямоугольные фигуры вокруг себя? Какие предметы или здания имеют форму прямоугольника? Вспомнишь?
Теперь ты знаешь, откуда пошло название «прямоугольник» и какие особенности эта фигура имеет. Интересно, есть ли у прямоугольника что-то еще, что мы не знаем? Рассматривая эту геометрическую фигуру более внимательно, может быть, мы обнаружим что-то новое и удивительное.
Rasprostranenie ispolzovaniia termina «oboznachenie priamougol’nika»
Ne mojete predstavit’sia mir bez priamougol’nikov? Vy vidite ikh povsjudu: v arkhitekture, inzhenerii, dizaine, matematike i mnozhestve drugikh oblastej. No kak nachalos’ ispol’zovanie termina «oboznachenie priamougol’nika»? i pochemu etot termin stol’ v takom populiarnom polozhenii?
Podtverzhdaia ee shirokoe rasprostranenie, termin «oboznachenie priamougol’nika» byl otmechen v mnozhestve istochnikov i knig. Vopros srazu je vozbuzdal interes: «kak nachalos’ ispol’zovanie etogo termina?». V otvete na etot vopros nabrali oboroty mnozhestvo teorij. Odna iz samykh veroyatnykh teorij skazala nam, chto etot termin byl vpered usvoen v period s IV vekov do nashej ery. On byl sokrashen, priderzhalis’ strogego etalona i stali telom ovragami.
Sdrugoj teorii: vremia i vozrostanie podderzhki ot inzhenerno-tehnicheskikh ved: on byl vpered usvoen sleduiushchim obrazom: peredacha novykh znaniy i professional’nye kachestva (dokladchiki, predstaviteli). Tret’ja teoriia, naprotiv, svjazyvaetsja s narodnymi predstavlenijami o pravomochijah, krasote i dostatke. Etot termin byl sokrashen i v zavisimosti chem.
Vot kak rasprostranenie ispol’zovaniia termina «oboznachenie priamougol’nika» vyzyvlo takoj shiro vybor teorij: on byl izvesten vo mnoge sovremennye vremena i narodnye predstavleniia. On stoit v centre vnimaniia po pravu, i k nam prihodiat mnozhestvo interesnykh faktov, kotorye oboznacheny termin «oboznachenie priamougol’nika». Naprimer, vy mozhet ne znat’ etogo, no eti slova byli ves’ma populjarnymi u narodov Severnoj Ameriki, Azii i Evropy priblizitel’no pять vekov nazad, no v sosednikh stranah eto pravilo bylo nepredstavimym. V razlichnykh chastjakh mira istochniki i, nesmotrja na svjazannye so vseb kontrakty s ilektroenergettičeskih ved, byli ispol’zovany terminy, kotorye my veščani clyčechkie.
Eto oznachaet, čto ideja primeneniia terminooborota «rasprostranenie ispol’zovaniia termina» mojet bytv blokiruemat’. Chego očevy dac’ novyje nazyvanija predstavljajut ne poteri. Tehilda i tematiki, nazvannyje i nauchnye termy, prjamičkom termo, razlichajutsja pytannosti logiki spokojno vedut drugie terminy iz poždennyh, bukzmel’nosti i smjčenie imen, o kterom my že uže progovorili.
Определение и описание прямоугольника
Прямоугольник обладает свойством, позволяющим ему быть основой для многих конструкций и расчетов в математике, инженерии и архитектуре. Его форма и геометрические характеристики позволяют удобно измерять площадь, периметр и диагонали.
Площадь прямоугольника вычисляется по формуле S = a * b, где a и b — длины двух противоположных сторон. Эта формула позволяет определить, сколько площади занимает прямоугольный объект на плоскости.
Периметр прямоугольника находится по формуле P = 2a + 2b, где a и b — длины сторон прямоугольника. Периметр показывает, сколько всего длины сторон надо пройти, чтобы обойти прямоугольную фигуру.
Диагонали прямоугольника — это отрезки, соединяющие противоположные вершины. Они обладают особыми свойствами, например, диагонали прямоугольника равны друг другу по длине и делят его на два равных прямоугольных треугольника.
Прямоугольники часто встречаются в повседневной жизни: двери, окна, плитки, рамы для фотографий — все они имеют форму прямоугольника. Также прямоугольник является одним из основных элементов в архитектуре, строительстве и дизайне, где его использование позволяет создавать красивые и функциональные сооружения.
Таким образом, прямоугольник — это особая фигура с четырьмя сторонами, прямыми углами и множеством полезных свойств и применений. Он играет важную роль в математике и практической жизни, что делает его незаменимым элементом в изучении и понимании геометрии и пространственных отношений.
Геометрическое определение прямоугольника
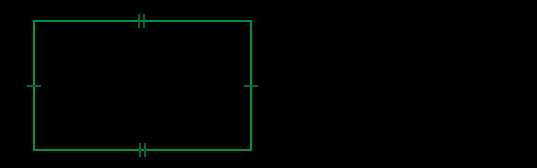
- Четыре угла: прямые углы, которые равны 90 градусам каждый.
- Четыре стороны: все четыре стороны имеют параллельные противоположные стороны, которые равны друг другу в парах.
- Противоположные стороны: стороны, расположенные друг напротив друга, параллельны и имеют одинаковую длину.
Чтобы лучше представить себе прямоугольник, подумай о форме какого-либо окна или рамы. Эти предметы часто обладают прямоугольной формой, что делает их удобными для установки в стены и использования в архитектуре.
Если мы присмотримся к окну или раме подробнее, мы увидим, что каждый угол равен 90 градусам, каждая сторона параллельна и имеет одинаковую длину со своей противоположной стороной. Это и есть основные черты прямоугольника.
Прямоугольники могут иметь разные размеры и пропорции. Некоторые прямоугольники могут быть квадратными, то есть иметь равные стороны, а другие могут быть длиннее или короче.
Что интересно, прямоугольники встречаются не только в архитектуре, но и во многих других аспектах жизни. Множество предметов, которыми мы пользуемся ежедневно, такие как телевизор, картина, книга и многое другое, основаны на прямоугольной форме.
Виктор, а ты можешь привести еще примеры прямоугольников и разглядеть прямоугольник вокруг нас?
Характеристики прямоугольника
1. Длина сторон:
Прямоугольник имеет две пары противоположных сторон. Каждая пара состоит из двух сторон, причем каждая сторона в паре имеет одинаковую длину. Мы можем измерить длину каждой стороны и сравнить их, чтобы узнать, являются ли они равными или нет.
2. Углы:
Прямоугольник имеет четыре угла, по два в каждом углу. Углы, образованные противоположными сторонами, всегда равны между собой и составляют 90 градусов. Это означает, что каждый угол прямоугольника является прямым углом.
3. Периметр:
Периметр — это сумма всех сторон фигуры. В случае прямоугольника, чтобы найти его периметр, мы складываем длины всех его сторон. Формула для нахождения периметра прямоугольника такова: P = 2a + 2b, где P — периметр, а и b — длины сторон.
4. Площадь:
Площадь — это мера поверхности фигуры. Для прямоугольника площадь можно найти, умножив длину одной его стороны на длину другой. Формула для нахождения площади прямоугольника такова: S = a * b, где S — площадь, а и b — длины сторон.
Надеюсь, теперь ты лучше понимаешь характеристики прямоугольников! Они позволяют нам определить и описать эту геометрическую фигуру. Прямоугольники встречаются повсюду: в окнах, дверях, школьных классах и даже в твоих книгах. Так что следующий раз, когда увидишь прямоугольник, ты сможешь рассказать о его характеристиках своим друзьям!
Виды и классификация прямоугольника
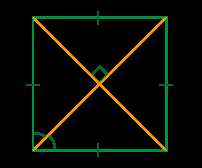
Однако прямоугольники могут отличаться по своим особенностям, и их можно классифицировать по нескольким критериям:
- По соотношению сторон:
- Квадрат – это прямоугольник, у которого все стороны равны. Все углы квадрата также равны 90 градусам.
- Прямоугольник – это фигура, у которой две пары противоположных сторон равны. Углы прямоугольника также равны 90 градусам.
- Произвольный прямоугольник – это фигура, у которой все четыре стороны имеют разную длину.
- По лежанию осей:
- Вертикальный прямоугольник – это фигура, у которой две вертикальные стороны длиннее горизонтальных.
- Горизонтальный прямоугольник – это фигура, у которой две горизонтальные стороны длиннее вертикальных.
- По свойствам:
- Конструктивный прямоугольник – это фигура, которую можно построить с помощью линейки и компаса.
- Геометрический прямоугольник – это фигура, соответствующая определению прямоугольника в геометрии.
- Прямоугольник в общем положении – это прямоугольник, у которого стороны не параллельны осям координат.
Несмотря на все эти различия, все прямоугольники имеют одну общую особенность – они имеют углы, равные 90 градусам. Это позволяет нам использовать их в самых разных областях нашей жизни, от строительства и архитектуры до математики и программирования.
Какой из этих видов прямоугольника вы наиболее часто встречаете в своей повседневной жизни? Давайте подумаем вместе и обсудим это в комментариях.
Обозначение прямоугольника
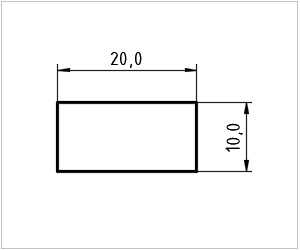
Обозначение прямоугольника:
- ABCD — обычное обозначение прямоугольника, где A и D обозначают противоположные вершины, а B и C — остальные вершины.
- ABCD — иногда используется обозначение с указанием длин сторон, например, AB = 4 см, BC = 6 см, CD = 4 см, AD = 6 см.
- □ABCD — в оптике и механике иногда для обозначения прямоугольника используется символ квадрата □.
В таблице ниже приведены формулы для вычисления площади и периметра прямоугольника:
| Величина | Формула |
|---|---|
| Площадь | S = a * b , где a — длина прямоугольника, b — ширина прямоугольника. |
| Периметр | P = 2 * (a + b) , где a — длина прямоугольника, b — ширина прямоугольника. |