Мы все иногда сталкиваемся с математическими операциями, которые могут причинять нам головную боль. Одним из таких является деление дробей на дроби. Но не беспокойтесь, в этом руководстве я помогу вам разобраться в этом процессе. Во-первых, вам необходимо умножить первую дробь на обратную второй дроби. Затем вы сокращаете полученную дробь до простейшего вида, если это возможно.
Давайте разберемся на примере. Предположим, у вас есть дробь 3/4, которую нужно разделить на дробь 1/2. Сначала мы умножим 3/4 на обратную 1/2, то есть на 2/1. Получится (3/4) * (2/1), что равно (3*2)/(4*1), то есть 6/4. Теперь мы можем сократить эту дробь, поделив числитель и знаменатель на их НОД (наибольший общий делитель), который равен 2. Итак, 6/4 становится 3/2.
Таким образом, чтобы разделить дробь на дробь, следуйте этим простым шагам: умножьте первую дробь на обратную к второй, и сократите полученную дробь до простейшего вида. Не забывайте практиковаться, чтобы стать уверенным в этом процессе!
Как разделить дробь на дробь: ключевые шаги и правила
Разделение дроби на дробь может показаться сложной задачей, но на самом деле это довольно просто, если вы знаете несколько ключевых шагов и правил. Давайте разберемся вместе!
- Шаг 1: Приведите дроби к общему знаменателю. Чтобы разделить дробь на дробь, необходимо привести обе дроби к общему знаменателю. Для этого умножьте числитель и знаменатель каждой дроби на такое число, чтобы получить одинаковые знаменатели.
- Шаг 2: Разделите числители. После приведения дробей к общему знаменателю, разделите числители друг на друга. Просто поделите одно число на другое.
Это все! Вы разделили дробь на дробь. Не забывайте упрощать дроби, если это возможно. Например, если числитель и знаменатель имеют общие делители, их можно сократить.
Для лучшего понимания давайте рассмотрим пример. Представим, что у нас есть дробь 3/4 и мы хотим разделить ее на 1/2. Приведем дроби к общему знаменателю, умножив числитель и знаменатель первой дроби на 2, а второй — на 4. Получаем 6/8 и 4/8. Затем разделим числители: 6 ÷ 4 = 1,5. Таким образом, результатом деления дроби 3/4 на 1/2 будет 1,5.
Надеюсь, это объяснение помогло вам понять, как разделить дробь на дробь. Практикуйтесь с разными примерами, чтобы укрепить свои навыки. Удачи вам!
Шаг 1: Нахождение общего знаменателя
Выкладывать фрагменты в виде дробей может показаться сложным для некоторых из нас. Но не волнуйтесь, это вовсе не так страшно!
Первым шагом, чтобы разделить дробь на дробь, мы должны найти общий знаменатель. Но что вообще такое общий знаменатель? Это просто число, которое является общим кратным знаменателей у обеих дробей.
Давайте рассмотрим пример. Представим, что у нас есть две дроби: 1/4 и 2/3. Чтобы найти общий знаменатель, мы должны найти число, на которое можно поделить и знаменатель 4, и знаменатель 3 без остатка. В данном случае, это число равно 12.
Как же мы найдем общий знаменатель? Просто умножьте знаменатели обеих дробей и результатом будет общий знаменатель. В нашем примере: 4 * 3 = 12. Итак, общий знаменатель для нашей пары дробей равен 12.
Теперь, когда мы нашли общий знаменатель, мы можем перейти ко второму шагу — привести дроби к общему знаменателю.
Шаг 2: Преобразование дробей к общему знаменателю
Теперь, когда мы разобрались с определением дробей и операцией деления, пришло время перейти ко второму шагу: преобразованию дробей к общему знаменателю. Представьте себя в роли шеф-повара и подумайте о дробях как о ингредиентах для вашего кулинарного шедевра. Чтобы объединить их в одну вкусную смесь, вам нужно использовать одинаковые порции.
В математике это обозначает, что вам нужно привести две или более дроби к такому виду, чтобы у них был одинаковый знаменатель. Как это сделать? Непросто, но мы держим за вас кулаки! Самый простой способ — найти общий знаменатель путем перемножения всех знаменателей дробей. Например, если у вас есть дроби 1/2 и 3/4, вы можете найти их общий знаменатель, умножив 2 и 4, что даст вам 8. Теперь вам нужно преобразовать каждую дробь так, чтобы она имела знаменатель 8. Для первой дроби это означает умножить числитель и знаменатель на 4, а для второй дроби — умножить числитель и знаменатель на 2.
Теперь, когда у вас есть две дроби с общим знаменателем, вы можете перейти к следующему шагу: выполнить операцию деления, разделив числители и знаменатели дробей. Ознакомьтесь с шагом 3, чтобы узнать больше!
Шаг 3: Вычитание дробей
Например, давайте вычтем 1/4 из 3/4. Здесь знаменатели уже одинаковы, поэтому нам не нужно выполнять преобразования. Просто вычтем числители: 3 — 1 = 2. Ответ: 2/4. Обратите внимание, что наш ответ можно упростить, деля числитель и знаменатель на их общий делитель, в данном случае это 2. Получим: 1/2.
Как вы видите, вычитание дробей — не такая уж сложная операция, главное следовать указанным шагам и быть внимательными. Теперь попробуйте сами решить несколько примеров! Удачи!
Шаг 4: Сокращение получившейся дроби
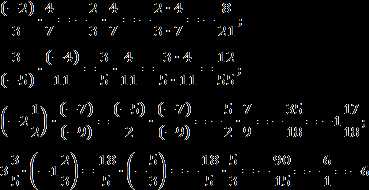
Когда мы разделили одну дробь на другую и получили результат, возможно, нам надо будет сократить эту дробь. Чтобы сократить дробь, нужно найти наибольший общий делитель (НОД) числителя и знаменателя и разделить оба числа на этот НОД.
Например, если у нас есть дробь 8/12, мы можем найти НОД чисел 8 и 12, который равен 4. Затем мы делим числитель и знаменатель на 4 и получаем дробь 2/3.
Сокращение дроби является важным шагом, который помогает нам упростить выражение и получить более понятный результат. Кроме того, сокращение позволяет нам работать с более маленькими числами, что может упростить последующие вычисления.
Итак, запомните, что когда вы разделяете одну дробь на другую, всегда проверяйте, нужно ли сокращать получившуюся дробь. Если да, найдите НОД числителя и знаменателя и разделите оба числа на этот НОД.
Шаг 5: Преобразование в правильную дробь
Теперь, когда мы разделили одну дробь на другую и получили несократимую десятичную дробь, самое время преобразовать ее в правильную дробь. Что это значит и как это сделать?
Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, 3/5 или 7/8. Наша несократимая десятичная дробь может быть представлена в виде десятичного числа с остатком. Например, 1.25 или 0.75.
Чтобы преобразовать несократимую десятичную дробь в правильную дробь, нужно следующее:
- Определить количество цифр в десятичной дроби после запятой. Назовем это количество n.
- Умножить десятичную дробь на 10^n, чтобы получить целое число без запятой. Например, если у нас есть несократимая десятичная дробь 0.75 и n = 2, мы умножим 0.75 на 100 и получим 75.
- Записать полученное число в числителе правильной дроби, а знаменатель оставить без изменений. В нашем примере, числитель будет 75, а знаменатель — 100.
- Дробь 75/100 можно сократить. Находим наибольший общий делитель для числителя и знаменателя и делим оба числа на него.
- Получаем окончательный результат: в нашем примере, 75/100 сократится до 3/4.
Таким образом, мы успешно преобразовали несократимую десятичную дробь в правильную дробь. Не забывайте проверять свои ответы и уверяйтесь, что они верны.
Шаг 6: Если возможно, дальнейшее сокращение дроби
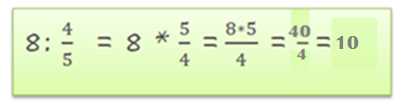
Так, мы уже добрались до шага 6 в нашем путешествии по разделению дроби на дробь! Вы справляетесь отлично! Теперь поговорим о возможности дальнейшего сокращения дроби.
Когда мы разделяем одну дробь на другую, мы иногда можем сократить полученную дробь до меньших частей. Это связано с тем, что числитель и знаменатель обеих дробей могут иметь общие делители. Например, если числитель и знаменатель новой дроби можно поделить на 2 без остатка, значит, мы можем сократить дробь на 2.
Но как найти общие делители числителя и знаменателя? Один из простых способов — разложить числитель и знаменатель на множители. Затем мы можем найти общие множители и использовать их для сокращения дроби.
Давайте рассмотрим пример. Допустим, у нас есть дробь 6/8, и мы хотим ее сократить. Разлагая числитель и знаменатель на множители, мы получаем: 6 = 2 * 3, 8 = 2 * 2 * 2. Замечаем, что у них есть общий множитель 2. Поделив числитель и знаменатель на 2, мы получим новую дробь: 3/4.
Таким образом, дальнейшее сокращение может помочь нам представить дробь в более простой и удобной форме. И помните, сокращение дроби — это всего лишь еще один шаг к полному решению математической задачи!