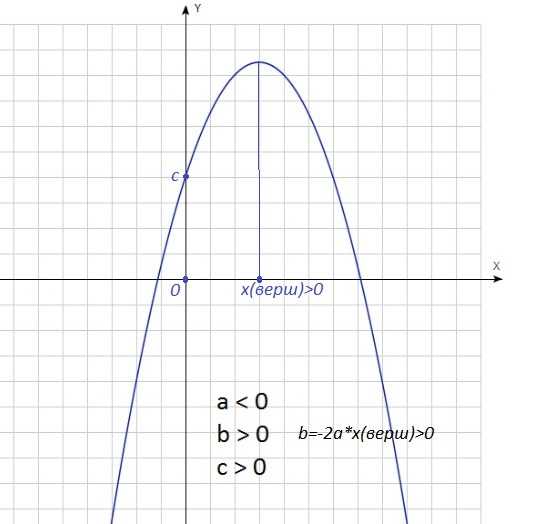
Коэффициент а в квадратичной функции — это один из ключевых параметров, определяющих форму графика данной функции. Он является коэффициентом при переменной второй степени и влияет на крутизну и направление этого графика. Значение коэффициента а может быть положительным, отрицательным или равным нулю, что приведет к различным формам кривой. Например, если а положительно, функция будет иметь параболу, открывающуюся вверх, а если а отрицательно, то парабола будет открываться вниз. Понимание значения коэффициента а позволяет нам анализировать и предсказывать поведение функции в зависимости от ее графика.
Определение квадратичной функции
В этих квадратичных функциях наиболее важным является коэффициент a, который определяет, насколько быстро кривая возрастает или убывает. Если коэффициент a положительный, то парабола открывается вверх и кривая возрастает. Если коэффициент a отрицательный, то парабола открывается вниз и кривая убывает. Величина коэффициента a также определяет крутизну параболы.
Коэффициенты b и c также играют важную роль в определении формы и положения параболы, но их влияние не так сильно, как у коэффициента a. Коэффициент b определяет сдвиг кривой по оси x, а коэффициент c — сдвиг по оси y.
Квадратичные функции широко используются в различных областях науки, инженерии и экономике для моделирования реальных явлений. Они помогают предсказать поведение системы и принимать оптимальные решения. Изучение квадратичных функций является важной частью курса алгебры и математики в целом.
Форма квадратичной функции
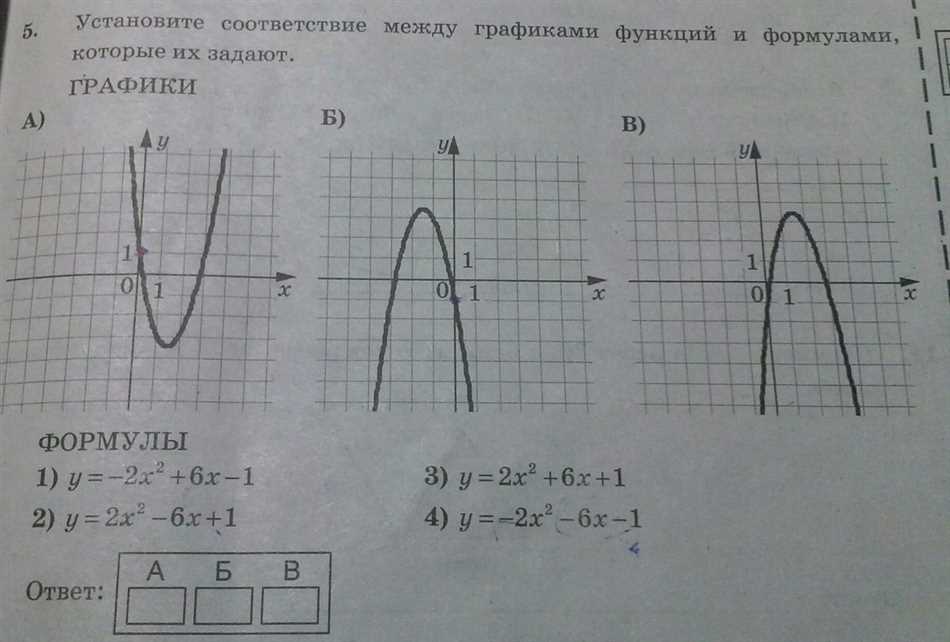
Коэффициент a важен, потому что он определяет направление открытия параболы, которая является графиком квадратичной функции. Если a > 0, то парабола открывается вверх, а если a < 0, то парабола открывается вниз. Таким образом, знак коэффициента a указывает на то, будет ли функция иметь минимум или максимум.
Если коэффициент a равен 1, то график функции будет симметричным относительно вертикальной прямой, проходящей через вершину параболы. В этом случае вершина имеет координаты (-b/2a, f(-b/2a)) и является экстремумом функции.
Квадратичная функция может принимать различные формы в зависимости от значений коэффициентов. Например, если коэффициент a положительный, а коэффициенты b и c равны нулю, то функция f(x) = ax^2 представляет собой параболу, открывающуюся вверх.
Если коэффициент a отрицательный, то форма функции будет отличаться. Например, функция f(x) = -ax^2 будет представлять параболу, открывающуюся вниз. Это примеры простейших функций, но в реальности коэффициенты могут принимать любые значения, и форма функции будет меняться соответственно.
Знание формы квадратичной функции важно для анализа ее свойств и использования в различных областях, таких как физика, экономика и инженерия. Кроме того, понимание формы функции помогает визуализировать математический объект и делает его более доступным для понимания. Поэтому изучение формы квадратичной функции является важным умением, которое может помочь в решении различных задач и проблем.
Значение коэффициента «а» в квадратичной функции
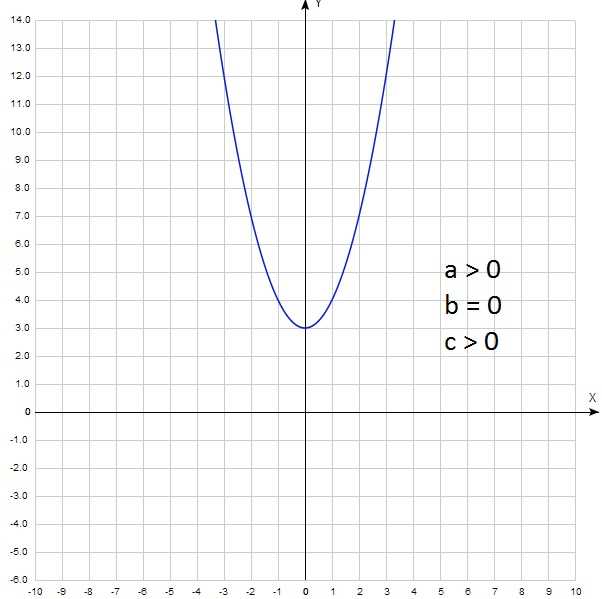
Если коэффициент «а» положительный, то парабола открывается вверх. Например, в квадратичной функции f(x) = ax^2 + bx + c, где «а» больше нуля, парабола будет смотреть вверх. Такие функции обычно имеют внизу «впадину» и называются вогнутыми вверх.
Если коэффициент «а» отрицательный, то парабола открывается вниз. Например, в функции g(x) = -ax^2 + bx + c, где «а» меньше нуля, парабола будет смотреть вниз. Такие функции обычно имеют сверху «пик» и называются вогнутыми вниз.
Когда же коэффициент «а» равен нулю, парабола становится прямой. Например, в функции h(x) = bx + c, где «а» равно нулю, график будет представлять собой прямую линию. Такая функция называется линейной, а парабола отсутствует.
Значение коэффициента «а» имеет влияние на множество характеристик квадратичной функции, таких как вершина параболы, направление ветвей, точки пересечения с осями координат и многое другое.
Но важно помнить, что для полного понимания и анализа квадратичной функции необходимо учитывать все ее коэффициенты, а не только «а». Каждый коэффициент выполняет свою роль и вносит свой вклад в общую картину функции.
Влияние коэффициента а на график функции
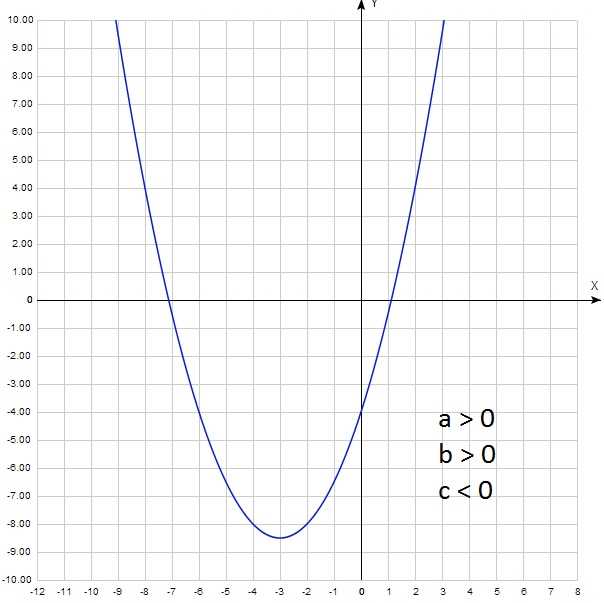
Коэффициент а в квадратичной функции играет ключевую роль в определении формы и положения графика этой функции. Он отвечает за крутизну и направление открытия параболы.
Если коэффициент а положительный, то парабола будет направлена вверх, образуя «улыбку», как у довольного искусителя. Это происходит потому, что при увеличении х, квадратичная функция с положительным коэффициентом а будет возрастать, а при уменьшении х — убывать.
Например, если у нас есть функция y = x^2, где коэффициент а равен 1, график будет открыт вверх и иметь форму «улыбки». Если увеличить а до 2, график будет более крутым и иметь больший размах. Таким образом, положительный коэффициент а увеличивает крутизну и размах параболы.
С другой стороны, если коэффициент а отрицательный, то парабола будет направлена вниз, образуя «грустные губы». При увеличении х, функция будет убывать, а при уменьшении х — возрастать.
Например, если у нас есть функция y = -x^2, где коэффициент а равен -1, график будет открыт вниз и иметь форму «грустных губ». Если увеличить а до -2, график будет более крутым и иметь больший размах. Таким образом, отрицательный коэффициент а также увеличивает крутизну и размах параболы, но в направлении вниз.
Во всех этих случаях, чем больше значение а, тем более стремительно меняется функция и тем шире размах параболы. Коэффициент а действительно играет важную роль в определении геометрических свойств графика квадратичной функции.
Коэффициент а в квадратичной функции: определение и значения

Значение коэффициента а может быть положительным, отрицательным или нулевым, влияя на форму и положение параболы.
1. Если коэффициент а положителен, то парабола открывается вверх и имеет выпуклую форму. Это означает, что значение функции увеличивается по мере увеличения значения переменной x.
2. Если коэффициент а отрицателен, то парабола открывается вниз и имеет вогнутую форму. В этом случае значение функции уменьшается по мере увеличения значения переменной x.
3. Если коэффициент а равен нулю, то квадратичная функция превращается в линейную функцию и парабола становится прямой линией, проходящей через точку (0, c). В этом случае парабола не имеет выпуклости или вогнутости.


