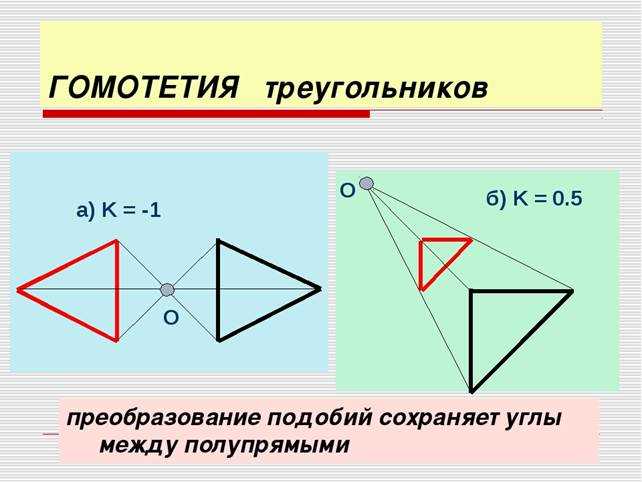
Коэффициент гомотетии: понятие, примеры и применение

Коэффициент гомотетии — это математический термин, который описывает отношение масштабов между двумя подобными геометрическими фигурами. Он показывает, насколько одна фигура увеличивается или уменьшается по сравнению с другой. Коэффициент гомотетии может быть положительным или отрицательным, в зависимости от направления изменения размеров.

Примером применения коэффициента гомотетии может служить изменение размеров географической карты. Если коэффициент гомотетии больше 1, то карта увеличится, а если меньше 1, то уменьшится. Также этот концепт используется в фотографии и дизайне, чтобы изменять размеры изображений без искажения пропорций.

Понимание коэффициента гомотетии позволяет нам увидеть, как изменение размеров влияет на форму и структуру объектов, что является важным во многих областях науки и промышленности.

Определение коэффициента гомотетии

Для понимания концепции коэффициента гомотетии, давайте рассмотрим некоторые примеры. Представьте, что у нас есть две машины — одна маленькая и другая большая. Если маленькая машина имеет длину 3 метра, а большая машина имеет длину 6 метров, то коэффициент гомотетии между ними равен 2. Это означает, что маленькая машина в два раза меньше по размеру, чем большая машина.

Коэффициент гомотетии может быть больше 1, что указывает на увеличение размера, или меньше 1, что указывает на уменьшение размера. Например, если у нас есть две картины — одна 40 см в высоту, а другая 20 см в высоту — коэффициент гомотетии будет равен 0.5. Это означает, что наша вторая картина в два раза меньше по размеру, чем первая.

Коэффициент гомотетии также может быть отрицательным, что указывает на зеркальное отражение фигуры. Например, если у нас есть два треугольника — один повернут на 180 градусов по отношению к другому — коэффициент гомотетии будет равен -1.

Коэффициент гомотетии имеет множество применений в геометрии, физике, экономике и других науках. Он позволяет нам анализировать изменения в размерах фигур, делать предсказания и прогнозы, а также находить пропорции между различными объектами.

В заключении, коэффициент гомотетии является важным математическим понятием, которое помогает нам понять масштабные изменения фигур. Он позволяет нам увидеть, насколько одна фигура увеличивается или уменьшается по сравнению с другой, и имеет широкий спектр применений в науке и повседневной жизни.

Общее определение коэффициента гомотетии

В простом понимании, коэффициент гомотетии показывает, во сколько раз одна фигура увеличивается или уменьшается относительно другой. Например, если коэффициент гомотетии равен 2, это означает, что вторая фигура вдвое больше первой.

Коэффициент гомотетии обозначается буквой «k» и может быть как положительным, так и отрицательным числом. Положительный коэффициент гомотетии указывает на увеличение размеров фигуры, а отрицательный — на их уменьшение и зеркальное отражение.

Этот математический концепт широко применяется в различных областях, включая геометрию, физику, экономику и графический дизайн. Например, в геометрии коэффициент гомотетии используется для нахождения подобных треугольников или плоских фигур. А в экономике он может быть использован для анализа изменения размеров производства или рынков.

Задайте себе вопрос: Какую роль коэффициент гомотетии может сыграть в вашей области деятельности? Какие примеры масштабирования вы можете найти в своей повседневной жизни или работе?

Формула для вычисления коэффициента гомотетии

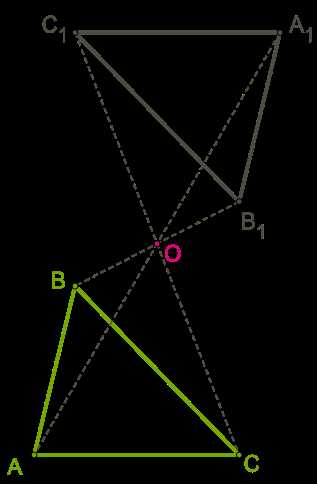
Если дана фигура соответственно точкам A и A’ на плоскости и мы знаем, что коэффициент гомотетии равен k, то для нахождения k необходимо использовать формулу:

k = AB’ / AB

Здесь AB’ — новое расстояние между соответствующими точками, а AB — изначальное расстояние между ними.

Давайте рассмотрим пример для лучшего понимания формулы. Представьте, что у вас есть фигура, состоящая из трех точек: A, B и C. Вы применяете гомотетию к этой фигуре и получаете новую фигуру с точками A’, B’ и C’. Вы хотите найти коэффициент гомотетии для этой трансформации.

Вам известны значения расстояний AB’ и AB. Подставьте эти значения в формулу k = AB’ / AB и вычислите результат.

Таким образом, формула для вычисления коэффициента гомотетии позволяет нам определить во сколько раз изменится пространство при гомотетии. Это полезное инструмент при решении задач в геометрии, а также при работе с графиками и объектами, требующими изменения масштаба.

Примеры коэффициента гомотетии

Пример 1: Увеличение и уменьшение фигуры

Представьте себе квадрат со стороной 2 см. Если мы увеличим его размеры в 2 раза, то стороны станут равными 4 см. В этом случае коэффициент гомотетии равен 2, так как мы увеличили размеры фигуры вдвое.

Наоборот, если мы уменьшим квадрат с размерами 4 см до 2 см, то коэффициент гомотетии будет равен 0,5, так как масштаб уменьшился вдвое.

Пример 2: Фигуры разных форм

Коэффициент гомотетии также может применяться к фигурам разных форм. Например, у нас есть треугольник со сторонами 3 см, 4 см и 5 см, и мы хотим увеличить его размеры в 3 раза. В этом случае новые стороны будут равными 9 см, 12 см и 15 см, и коэффициент гомотетии будет равен 3.

Пример 3: Гомотетия в экономике

Коэффициент гомотетии также играет важную роль в экономике. Например, предположим, что цена товара увеличивается в 10%, и в результате спрос на него снижается на 20%. В этом случае коэффициент гомотетии будет равен -0,2, что означает, что спрос сократился на 20% от оригинального объема за каждый процент увеличения цены.

Коэффициент гомотетии — это мощный инструмент для понимания и изучения пропорциональных отношений в различных областях. Он помогает нам представить и анализировать изменения размеров и объемов фигур, предметов, показателей и экономических параметров. Используя коэффициент гомотетии, мы можем привести различные данные к одной шкале, что помогает нам видеть и понимать их сравнительные отношения.

Примеры коэффициента гомотетии в геометрии

Давайте рассмотрим некоторые примеры, чтобы лучше понять, как работает коэффициент гомотетии.

Пример 1:

Представьте, что у нас есть окружность радиусом 5 см. Если мы применим гомотетическое преобразование с коэффициентом гомотетии 2, это означает, что новая окружность будет иметь радиус размером в 2 раза больше. Радиус новой окружности будет составлять 10 см.

Пример 2:

Допустим, у нас есть треугольник с длинами сторон 4 см, 5 см и 6 см. Если мы применим гомотетическое преобразование с коэффициентом гомотетии 3, то каждая сторона увеличится в 3 раза. Новые длины сторон будут составлять 12 см, 15 см и 18 см соответственно.

Пример 3:

Представьте себе прямоугольник со сторонами 10 см и 5 см. Если мы применим гомотетическое преобразование с коэффициентом гомотетии 0,5, это означает, что каждая сторона будет уменьшена в 2 раза. Таким образом, новые стороны прямоугольника будут иметь длину 5 см и 2,5 см.

Пример 4:

Представим, что у нас есть квадрат со стороной 8 см. Если мы применим гомотетическое преобразование с коэффициентом гомотетии 1,5, то каждая сторона будет увеличена в 1,5 раза. Новая длина стороны будет составлять 12 см.

Определение и понимание коэффициента гомотетии в геометрии важно не только для того, чтобы понять примеры, но и для решения задач, связанных с масштабированием фигур. Коэффициент гомотетии помогает определить, как изменятся размеры и форма фигуры при гомотетическом преобразовании.

Примеры коэффициента гомотетии в экономике

• Коэффициент увеличения производства – один из основных примеров коэффициента гомотетии в экономике. Когда производственные мощности предприятия увеличиваются в фиксированной пропорции, это может привести к изменению масштабов производства и соответствующему росту выручки. Например, если производительность труда на предприятии возрастает на 10%, то выручка может увеличиться в несколько раз больше.

• Коэффициент эластичности спроса – еще один пример применения коэффициента гомотетии в экономике. Эластичность спроса изучает, насколько изменяется количество товаров или услуг в ответ на изменение их цены. Если коэффициент эластичности больше 1, то спрос является эластичным, что означает, что даже небольшие изменения в цене могут вызвать значительные изменения в объеме спроса. Например, если цена на товар увеличивается на 10%, а спрос снижается на 20%, то коэффициент эластичности будет равен 2.

• Коэффициент долевого участия – еще один интересный пример гомотетии в экономике. В случае совместного предприятия или партнерства между двумя или более компаниями, коэффициент долевого участия определяет процентное соотношение доли каждого участника в прибыли или убытке. Например, если один участник имеет 60% долю, а другой – 40%, то коэффициент долевого участия будет соответственно равен 0.6 и 0.4.

Это только некоторые примеры применения коэффициента гомотетии в экономике. Он широко используется в исследованиях ценообразования, спроса, предложения, производства и других экономических процессах. Понимание и использование коэффициента гомотетии помогает экономистам и бизнес-аналитикам в анализе и прогнозировании экономических явлений и принятии эффективных решений.

Применение коэффициента гомотетии

1. Архитектура и дизайн

Коэффициент гомотетии широко используется в архитектуре и дизайне для создания пропорциональных и гармоничных объектов. Например, при проектировании зданий, архитекторы могут применять гомотетию для масштабирования и изменения размеров здания без искажения его формы. Также, при создании дизайнерских предметов интерьера, мебели или одежды, гомотетия позволяет достичь эстетического баланса и создать впечатляющий внешний вид.

2. Моделирование физических явлений

Коэффициент гомотетии используется в физических и инженерных моделях для анализа и прогнозирования различных физических явлений, таких как обтекание тела жидкостью или распространение звука. Использование гомотетии позволяет упростить моделирование и получить более точные результаты.

3. Финансовая аналитика

Коэффициент гомотетии также находит применение в финансовой аналитике. Например, при анализе динамики рыночных индексов или финансовых показателей компаний, гомотетия может быть использована для определения общей тенденции и прогнозирования будущих изменений. Это позволяет инвесторам и аналитикам принимать более обоснованные решения на основе статистических данных.

4. Картография и география

В картографии и географии коэффициент гомотетии используется для изменения масштаба карты или глобуса. С помощью гомотетии можно увеличить или уменьшить карту таким образом, чтобы она соответствовала определенному масштабу или позволяла более детально изучать определенную территорию.

5. Бизнес-планирование

Гомотетия может быть полезной в бизнес-планировании. Например, при разработке стратегии развития компании, коэффициент гомотетии может использоваться для определения роста и масштабирования бизнеса. Анализ шкалы изменений, таких как численность персонала, объем производства или продаж, позволяет прогнозировать потенциальные результаты и принимать решения, направленные на достижение поставленных целей.

Вот некоторые основные области, где коэффициент гомотетии находит практическое применение. Однако этот список не является исчерпывающим, и существуют и другие сферы, где гомотетия играет важную роль. В итоге, понимание и использование коэффициента гомотетии помогает нам лучше понять, описать и прогнозировать различные явления и процессы в нашем мире.

Применение коэффициента гомотетии в оптике

Оптика – это наука, изучающая свойства света и его взаимодействие с различными объектами и средами. Коэффициент гомотетии в оптике используется для описания изменения размеров и формы оптических объектов и изображений.

Один из примеров применения коэффициента гомотетии в оптике – это увеличение или уменьшение масштаба линз. Линзы – это оптические элементы, которые преломляют свет, позволяя нам видеть изображения так, как они есть. Коэффициент гомотетии может быть использован для регулирования размера этих изображений. Например, с помощью изменения коэффициента гомотетии можно увеличить изображение, сделав его более крупным и детальным.

Другой пример применения коэффициента гомотетии в оптике – это настройка объективов камер и микроскопов. Оптические системы этих устройств используются для получения увеличенных изображений объектов. Коэффициент гомотетии позволяет регулировать масштаб этих изображений, обеспечивая большую глубину резкости и более четкую передачу деталей.

Коэффициент гомотетии также может быть применен для определения расстояния от глаза до изображения в оптических устройствах, таких как очки или телескопы. Эта информация позволяет оптимизировать фокусировку и обеспечивает более комфортное восприятие изображений.

Коэффициент гомотетии: определение, примеры и применение

Коэффициент гомотетии обозначается символом k. Если k > 1, то фигура увеличивается, если 0 < k < 1, то фигура уменьшается, а если k = 1, то фигуры подобны с коэффициентом пропорциональности равным 1.

Примеры применения коэффициента гомотетии:

• В геометрии коэффициент гомотетии используется для определения подобия фигур и решения задач на нахождение неизвестных сторон или углов.
• В топологии коэффициент гомотетии применяется для описания свойств отображений между топологическими пространствами.
• В макроэкономике коэффициент гомотетии используется для оценки влияния изменения масштаба на объем производства и доходы компаний.

Таким образом, коэффициент гомотетии является важным понятием в различных областях науки и практики, где важно определить отношение масштабов между объектами или явлениями.