Коэффициенты в алгебре: основные понятия и определения

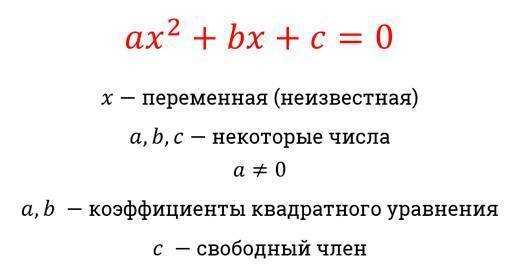
В алгебре, коэффициенты – это числа, которые умножаются на переменные, известные как алгебраические термы. Коэффициенты помогают нам понять, как именно влияют переменные на выражение или уравнение.

Коэффициенты используются в различных математических операциях, включая сложение, вычитание, умножение и деление. Они также играют важную роль в решении систем уравнений и нахождении корней.

Коэффициенты могут быть положительными, отрицательными или нулевыми. Они могут представляться числами или буквами, в зависимости от контекста задачи. Коэффициенты позволяют нам выявлять закономерности и устанавливать связи между переменными в алгебраических выражениях и уравнениях.

Понимание коэффициентов в алгебре является фундаментальным в математике и играет важную роль в практическом применении алгебры в различных областях, таких как физика, экономика, инженерия и технические науки.

Основные понятия и определения коэффициентов в алгебре

Коэффициенты — это числа, умножающиеся на переменные в математических выражениях и уравнениях. Они помогают построить связь между переменными и выражениями, позволяют вычислять значения и анализировать свойства.

Коэффициенты могут быть использованы для решения уравнений и систем уравнений, нахождения общих факторов, построения графиков и моделирования различных явлений.

В алгебре коэффициенты имеют различные названия в зависимости от того, как они используются:

• В линейных уравнениях коэффициент при переменной определяет ее вклад в итоговый результат.
• В многочленах коэффициенты при степенях переменной указывают на коэффициенты при каждой степени.
• В системах уравнений коэффициенты определяют отношения между переменными.

В общем виде, коэффициенты в алгебре — это числа, которые помогают нам анализировать и решать математические задачи. Они играют важную роль в решении проблем и прогнозировании результатов. Понимание и использование коэффициентов помогает нам лучше понять мир вокруг нас и принять более информированные решения.

Что такое коэффициенты в алгебре?

Представь, что ты развлекаешься весь день, играя в футбол, а твоя мама не знает, сколько времени ты провел на улице. Как было бы полезно иметь некоторую информацию о продолжительности игры, чтобы устроить аргументированную беседу с ней о допустимом времени на улице, а не получать только благосклонные или суровые реакции без объяснений.

В алгебре, коэффициенты — это подобная идея. Во время решения уравнений, которые в общих чертах выражают соотношения между различными числами или величинами, мы используем коэффициенты, чтобы понять, как каждое число или переменная влияет на решение.

Коэффициенты позволяют нам определить важность и вклад каждого элемента в уравнении. Это как магический инструмент, который помогает нам понять, сколько различных составляющих влияют на результат.

В основном, коэффициенты — это числа, которые умножаются на переменные или другие члены уравнений. Они показывают, как сильно каждый элемент влияет на решение. Благодаря коэффициентам, мы можем анализировать и предсказывать результаты уравнений, что очень полезно в разных областях жизни, таких как финансы, физика и экономика.

• Итак, очень важно понимать, что такое коэффициенты в алгебре, потому что они являются ключом к пониманию и анализу сложных уравнений.
• Они позволяют нам оценить, как каждая переменная или число в уравнении влияет на итоговый результат.
• Коэффициенты играют важную роль в науке, экономике, физике и многих других областях, где требуется анализ числовых данных и решение сложных уравнений.

Роль коэффициентов в алгебраических выражениях

Коэффициенты позволяют нам выразить зависимость между различными переменными. Они помогают нам решать уравнения и системы уравнений, исследовать свойства функций и находить значения переменных в конкретных ситуациях.

Коэффициенты также имеют физическую интерпретацию. Например, в физике они могут представлять физические величины, такие как скорость, ускорение или коэффициент трения. В экономике они могут представлять степень зависимости между различными переменными, например, коэффициент спроса или коэффициент эластичности.

Интересно то, как математика находит свое применение в различных областях нашей жизни. Без коэффициентов мы бы не смогли смоделировать и анализировать сложные явления, выявлять закономерности и принимать обоснованные решения.

Какие виды коэффициентов существуют в алгебре

Другим важным видом коэффициентов являются переменные коэффициенты. В отличие от числовых коэффициентов, переменные коэффициенты зависят от контекста и могут изменяться в зависимости от условий задачи. Например, в выражении ax + by, буквы a и b являются переменными коэффициентами.

Также в алгебре существуют множители в виде констант или коэффициентов перед переменными. Например, в выражении 3x + 4y, числа 3 и 4 являются множителями.

Важным концептом в алгебре является также степень коэффициента, которая определяет, какая степень у переменной будет в выражении. Например, в выражении 2x^3 + 3x^2 + 4x + 5, степени коэффициентов равны 3, 2, 1 и 0 соответственно.

Заключение

Таким образом, знание и понимание коэффициентов в алгебре является неотъемлемой частью математического образования. Они помогают нам решать задачи и находить решения, а также расширяют наше понимание о математическом мире и его законах.