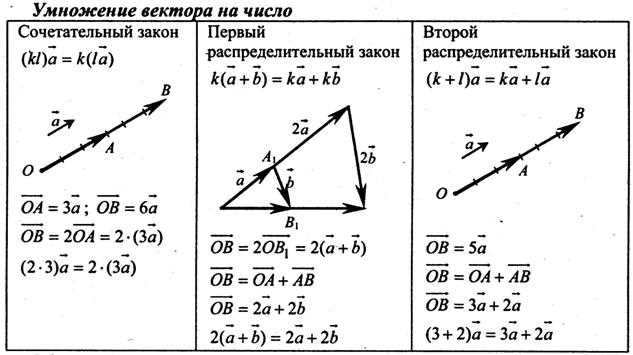
Векторы играют важную роль в геометрии и широко применяются в физике и других науках. Когда мы говорим о векторах, часто встречаются термины «коллинеарные» и «неколлинеарные». Что же они означают?
Коллинеарные векторы — это векторы, которые лежат на одной прямой. Если векторы можно представить как стрелки, то коллинеарные векторы будут направлены вдоль одной и той же прямой или противоположно ей. Это означает, что они имеют одинаковое направление или противоположное, но необходимо, чтобы их длины были пропорциональны.
Неколлинеарные векторы, наоборот, не лежат на одной прямой. Они могут быть направлены в разные стороны и иметь любой угол между собой. Важно отметить, что неколлинеарные векторы всегда будут линейно независимыми, то есть ни один из них не может быть выражен через другие с помощью умножения на число.
Понимание различий между коллинеарными и неколлинеарными векторами поможет нам лучше понять их свойства и применение в реальной жизни.
Определение вектора
Основные характеристики вектора — это направление и длина. Направление вектора обозначается стрелкой, которая указывает на его направление. Длина вектора обозначается модулем или абсолютной величиной и показывает, насколько далеко простирается вектор.
Векторы можно представить как точки в пространстве или как столбцы чисел, где каждое число соответствует координате вектора. Например, если вектор обозначается как (2, 3), это означает, что он имеет длину 2 и направление под углом 3 радианы к положительному направлению оси X.
Векторы можно складывать и вычитать, умножать на скаляр и находить их скалярное произведение. Сложение векторов происходит путем сложения их координат, а вычитание — путем вычитания координат. Умножение вектора на скаляр приводит к изменению его длины, а скалярное произведение векторов показывает взаимную зависимость между ними.
Векторы могут быть коллинеарными или неколлинеарными. Коллинеарные векторы лежат на одной прямой и имеют одно и то же направление или противоположное. Неколлинеарные векторы не лежат на одной прямой и имеют различные направления.
Коллинеарные векторы

Хорошо, теперь я расскажу тебе, что такое коллинеарные векторы. Коллинеарные векторы – это векторы, которые лежат на одной прямой или параллельны друг другу. Это значит, что если два или более вектора коллинеарны, то они направлены в одном и том же направлении или в противоположных направлениях.
Давай рассмотрим пример: представь, что ты рисуешь две стрелки на бумаге. Если их направления одинаковые или противоположные, они будут коллинеарными векторами. Например, одна стрелка направлена вверх, а вторая – туда же, или одна стрелка направлена вверх, а вторая – вниз. В этом случае эти две стрелки будут коллинеарными векторами.
Векторы могут иметь разную длину, но они все равно будут коллинеарными, если они лежат на одной прямой или параллельны друг другу. Сделай паузу и подумай, какие еще примеры коллинеарных векторов ты можешь представить.
Теперь давай поговорим о некоторых свойствах коллинеарных векторов. Когда два вектора коллинеарны, значит, один вектор может быть получен из другого путем умножения на скаляр. Например, если у нас есть вектор а, который равен (2,4), и вектор b, который равен (4,8), то вектор b можно получить умножением вектора a на 2, так как (2,4) * 2 = (4,8).
Коллинеарные векторы имеют также понятие пропорциональности. Это означает, что если два вектора коллинеарны, то их координаты имеют одинаковое отношение. Например, рассмотрим вектор a = (2,4) и вектор b = (4,8). Они коллинеарны, так как их координаты имеют отношение 1:2.
И последнее, что я хотел бы упомянуть, – это то, что коллинеарные векторы могут быть использованы для описания сил, например, в физике. Если векторы силы, действующие на объект, коллинеарны, то можно сказать, что силы направлены в одном направлении или в противоположных направлениях.
Надеюсь, ты теперь лучше понимаешь, что такое коллинеарные векторы и как они используются. Если у тебя остались вопросы, задавай их мне, и я с удовольствием на них отвечу!
Неколлинеарные векторы
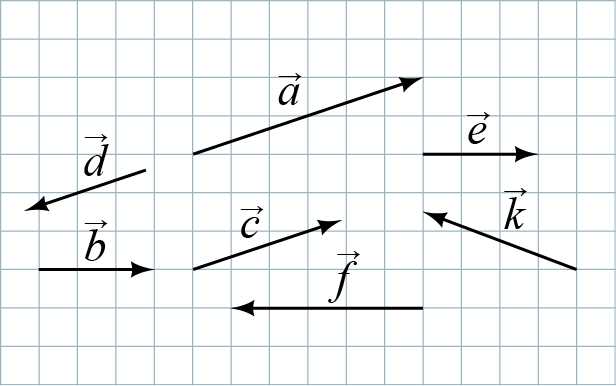
Неколлинеарные векторы – это векторы, которые не лежат на одной прямой. Другими словами, они не параллельны и не сонаправлены. Это важное понятие в геометрии, так как неколлинеарные векторы могут образовывать различные углы, и их сумма или разность может приводить к интересным результатам.
Для того чтобы определить, являются ли векторы неколлинеарными, можно воспользоваться геометрическими методами. Например, можно нарисовать векторы на координатной плоскости и проверить, лежат ли они на одной прямой. Если векторы не пересекаются и не лежат на одной прямой, то они будут неколлинеарными.
Можно также использовать алгебраические методы для проверки неколлинеарности векторов. Например, если два вектора \(A\) и \(B\) неколлинеарны, то они не могут быть пропорциональны друг другу. Если же между векторами существует линейная зависимость, то они будут коллинеарными.
Неколлинеарные векторы могут быть полезными при решении различных задач. Они могут помочь определить плоскость или пространство, на котором находится объект, и использоваться для нахождения углов, длин прямых или расстояний между точками.
Чтобы лучше понять это понятие, давайте рассмотрим пример. Представьте, что у вас есть два вектора \(A\) и \(B\), которые не лежат на одной прямой. Вы можете провести перпендикуляр из начала вектора \(A\) на вектор \(B\), и это будет третий вектор \(C\). Вектор \(C\) будет неколлинеарным с векторами \(A\) и \(B\), так как он не лежит на той же прямой.
Таким образом, неколлинеарные векторы открывают перед нами новые возможности в понимании геометрии пространства. Они помогают нам исследовать и понимать взаимоотношения и связи между различными объектами. Благодаря ним, мы можем решать задачи геометрии и физики, а также находить применение в других науках и областях жизни.
Критерии коллинеарности и неколлинеарности векторов
Коллинеарные векторы:
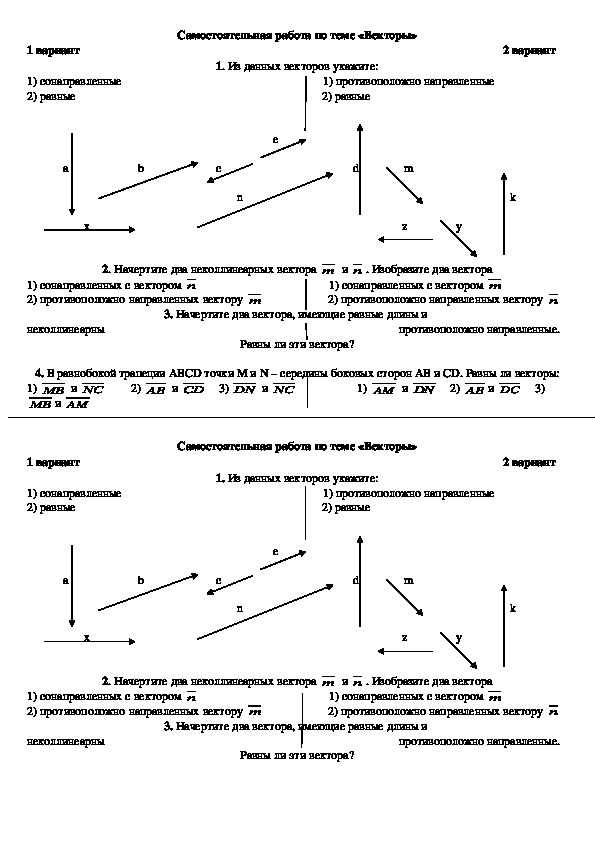
Векторы считаются коллинеарными, если они направлены в одном направлении или в противоположных направлениях. Другими словами, если два вектора лежат на одной прямой или их можно получить, умножая один вектор на любое число (положительное или отрицательное), то они коллинеарны. Например, если векторы a и b представляют движение автомобиля вперед и назад по одной и той же оси, то они будут коллинеарными.
Неколлинеарные векторы:
Векторы считаются неколлинеарными, если они не лежат на одной прямой. Другими словами, если два вектора не могут быть получены умножением одного на число, чтобы получить другой. Например, если векторы c и d представляют движение автомобиля по координатным осям X и Y, то они будут неколлинеарными.
Можно использовать несколько критериев для определения коллинеарности и неколлинеарности векторов:
- Угловой критерий: Если угол между двумя векторами равен 0° или 180°, то они коллинеарны. В противном случае они неколлинеарны.
- Линейный критерий: Если один вектор является линейной комбинацией другого вектора (т.е. может быть представлено в виде скалярного произведения или координатной линейной комбинации), то они коллинеарны. В противном случае они неколлинеарны.
Коллинеарные и неколлинеарные векторы широко применяются в различных областях, таких как физика, геометрия и инженерия. Например, векторы могут использоваться для определения направления силы, скорости объекта или перемещения в пространстве.
Важно знать критерии коллинеарности и неколлинеарности векторов, чтобы правильно решать задачи, связанные с их суммированием, разложением и прочими операциями. Помните, что коллинеарные векторы располагаются на одной прямой, в то время как неколлинеарные векторы не лежат на одной прямой.
Коллинеарные и неколлинеарные векторы: геометрия 9 класс
Коллинеарные векторы имеют одинаковое направление или противоположное направление. Если два вектора имеют одинаковое направление, они называются сонаправленными или параллельными. Если два вектора имеют противоположное направление, они называются противоположно направленными. Коллинеарные векторы могут быть равными по длине или иметь разную длину.
Неколлинеарные векторы не имеют общей точки и не лежат на одной прямой. Они могут иметь любое направление и любую длину. Неколлинеарные векторы могут пересекаться и образовывать углы между собой.
Примеры:
- Векторы AB и CD находятся на одной прямой и имеют одинаковое направление. Они являются коллинеарными векторами.
- Векторы EF и GH параллельны друг другу и имеют одинаковое направление. Они также являются коллинеарными векторами.
- Векторы IJ и KL не лежат на одной прямой и имеют разное направление. Они являются неколлинеарными векторами.
- Векторы MN и OP пересекаются, образуя угол между собой. Они также являются неколлинеарными векторами.
В геометрии 9 класса изучаются основные свойства коллинеарных и неколлинеарных векторов и их применение в различных задачах и решениях.



