Комплексные числа – это мощный математический инструмент, который активно применяется не только в математике, но и в физике. Они играют важную роль в решении различных задач, которые не могут быть эффективно решены с использованием только вещественных чисел.
Комплексные числа представляются в виде комбинации вещественной и мнимой частей, где мнимая единица обозначается символом «i». Они позволяют представить и работать с величинами, которые имеют как вещественную, так и мнимую составляющую.
В математике комплексные числа активно используются в алгебре и анализе. Они представляются в виде точек на комплексной плоскости и используются для решения уравнений, включая кубические и биквадратные уравнения. Комплексные числа также играют важную роль в теории функций и дифференциальных уравнений.
Комплексные числа также находят широкое применение в физике. Во многих физических явлениях, таких как электрические цепи, колебания и волны, магнетизм и электродинамика, комплексные числа являются неотъемлемой частью математических моделей и уравнений.
Таким образом, комплексные числа не только широко применяются в различных областях математики и физики, но и играют важную роль в решении сложных задач, которые не могут быть эффективно решены с использованием только вещественных чисел. Понимание комплексных чисел и их применение являются важными компетенциями для успешной работы в этих областях знаний.
Определение комплексных чисел
Когда вы впервые слышите о комплексных числах, они могут показаться странными и непонятными. Вы могли бы спросить себя: зачем нужны эти комплексные числа? И почему они так важны в математике и физике?
Давайте разберемся. Комплексные числа представляют собой мощный инструмент в математике и физике, позволяющий описывать и решать широкий спектр проблем, которые невозможно решить с помощью действительных чисел. Они используются во многих областях, таких как теория вероятностей, теория электрических цепей, управление системами и дифференциальные уравнения.
Одним из главных преимуществ комплексных чисел является их способность представлять и описывать векторные операции и фазовые углы. Формула Эйлера, одна из самых известных формул в математике, связывает тригонометрическую функцию с комплексными числами и позволяет легко работать с векторами и фазовыми углами.
Комплексные числа также широко используются в физике, особенно в области электромагнетизма и квантовой механики. Например, они используются для описания переходных процессов в электрических цепях, распространения электромагнитных волн и расчета энергетических уровней атомов.
Приведу вам один пример использования комплексных чисел. Допустим, вы хотите найти корень положительного числа. Используя действительные числа, вы не сможете найти его корень, потому что корень из отрицательного числа не существует в мире действительных чисел. Но если мы используем комплексные числа, мы можем найти его корень. Например, корень из -1 равен комплексному числу i. Это открывает перед нами новые возможности и позволяет решать задачи, которые раньше были неразрешимы.
Таким образом, комплексные числа играют фундаментальную роль в математике и физике, предоставляя нам мощный инструмент для решения сложных задач. Они позволяют нам моделировать и описывать реальный мир, а также разрабатывать новые теории и концепции. Независимо от того, занимаетесь ли вы математикой, физикой или какой-либо другой наукой, понимание комплексных чисел является необходимым для исследования фундаментальных принципов мира, в котором мы живем.
Базовые понятия и примеры
Основное свойство комплексных чисел — то, что их можно складывать, вычитать, умножать и делить друг на друга. Эти операции выполняются над каждой составляющей числа отдельно. Например, сложение комплексных чисел происходит путем сложения их действительных и мнимых частей: (a + bi) + (c + di) = (a + c) + (b + d)i.
Комплексные числа имеют широкое применение в математике и физике. Они используются для решения уравнений, анализа электрических цепей, а также в комплексном анализе, который изучает функции комплексных переменных.
Пример 1: Рассмотрим комплексное число 2 + 3i. Его действительная часть равна 2, а мнимая часть равна 3. Мы можем складывать это число с другими комплексными числами, например, (2 + 3i) + (4 + 2i) = 6 + 5i.
Пример 2: Рассмотрим уравнение x^2 + 4 = 0. Перепишем его в комплексной форме как x^2 + 4 = (x + 2i)(x — 2i) = 0. Это уравнение имеет два комплексных корня: x = 2i и x = -2i. Комплексные числа позволяют нам работать с такими уравнениями и находить их корни.
Иногда комплексные числа могут не иметь физического значения, но они все равно играют важную роль в математике. Возможность складывать, вычитать, умножать и делить комплексные числа расширяет наши возможности и позволяет решать более сложные задачи.
Алгебраическая форма комплексных чисел
Алгебраическая форма комплексных чисел исключительно важна в математике и физике, так как она позволяет выполнять все операции с комплексными числами, такие как сложение, вычитание, умножение и деление. Например, если у нас есть два комплексных числа в алгебраической форме a + bi и c + di, тогда их сумма будет равна (a + c) + (b + d)i.
Когда мы рассматриваем комплексные числа в алгебраической форме, мы можем сделать некоторые интересные наблюдения. Во-первых, действительная часть комплексного числа может быть равна нулю, что приводит к выражению вида bi. Такое комплексное число называется чисто мнимым. Например, число 3i является чисто мнимым числом.
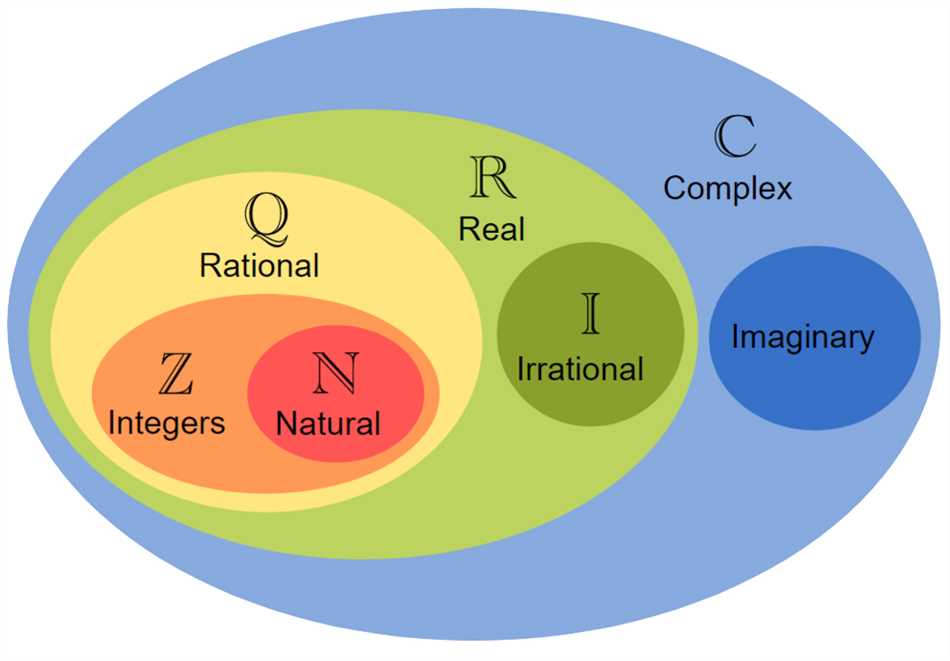
Во-вторых, если мы рассмотрим комплексное число вида a + 0i, то оно будет эквивалентно действительному числу a. Таким образом, комплексные числа обобщают действительные числа и дают нам больше возможностей в математике.
Наконец, важно отметить, что алгебраическая форма комплексных чисел является универсальным способом их представления и использования. Эта форма позволяет нам легко выполнять операции с комплексными числами и решать уравнения, включающие их. Она также находит применение в различных областях, таких как электротехника, квантовая механика и теория сигналов.
Геометрическая интерпретация комплексных чисел
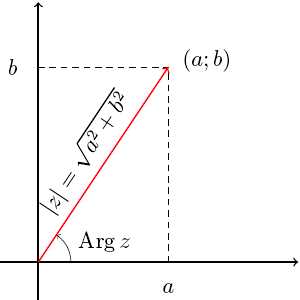
Главное достоинство геометрической интерпретации комплексных чисел заключается в том, что она позволяет легко визуализировать их свойства и операции над ними. Комплексная плоскость, также известная как плоскость Гаусса, используется для представления комплексных чисел. Вся комплексная плоскость может быть разделена на действительную ось и мнимую ось, которые пересекаются в начале координат.
Действительная часть комплексного числа представляет собой координату по оси а, а мнимая часть — координату по оси b. Таким образом, комплексное число a + bi представляется точкой (a, b) на комплексной плоскости.
Геометрическая интерпретация комплексных чисел позволяет нам выполнять операции сложения, вычитания, умножения и деления комплексных чисел в очень простой и интуитивной форме. Например, сложение комплексных чисел можно представить как сложение векторов на комплексной плоскости. Если мы сложим два комплексных числа a + bi и c + di, то результирующее комплексное число будет (a + c) + (b + d)i.
Также геометрическая интерпретация комплексных чисел дает нам возможность решать геометрические задачи с использованием комплексных чисел. Например, с помощью комплексных чисел мы можем легко определить длину отрезка в комплексной плоскости или угол между двумя векторами.
Геометрическая интерпретация комплексных чисел также находит применение в физике. Например, комплексные числа используются для представления и анализа колебаний и волн. Комплексные числа позволяют нам описывать фазу и амплитуду колебаний с помощью одного числа. Они также используются в электрических цепях и квантовой механике для решения физических задач.
Итак, геометрическая интерпретация комплексных чисел является неотъемлемой частью математики и физики. Она позволяет нам визуализировать их свойства, выполнять операции над ними и решать геометрические задачи. Комплексные числа имеют широкий спектр применений и оказывают большое влияние на различные области науки и техники.
Комплексные числа: важность и применение в математике и физике
Важность комплексных чисел в математике заключается в их способности решать уравнения, которые не имеют решений в обычных действительных числах. Они играют ключевую роль в комплексном анализе, теории функций и дифференциальных уравнений.
Применение комплексных чисел в математике:
- Решение алгебраических уравнений, например, кубического уравнения;
- Разложение рациональных функций на простейшие дроби;
- Решение систем линейных уравнений;
- Разложение функций в ряды Тейлора;
- Разработка и анализ электрических цепей;
- Теория вероятности и статистика.
Применение комплексных чисел в физике:

- Описание и анализ колебательных и волновых процессов;
- Расчет электрических цепей переменного тока;
- Анализ переменного тока и переменного напряжения в электрических системах;
- Описание магнитных полей и взаимодействия зарядов с полями;
- Анализ оптических явлений, таких как преломление и дифракция света;
- Описание квантовой механики и квантовых состояний.
Таким образом, комплексные числа играют важную роль в математике и физике, позволяя решать уравнения, описывать и анализировать физические явления и открывать новые области исследования.