Комплексные числа: сущность, применение и значение в математике

Математика – одна из самых удивительных наук, которая неразрывно связана с нашей повседневной жизнью. Одной из важных частей математики являются комплексные числа, которые играют значительную роль в решении сложных задач и моделировании реальных процессов.

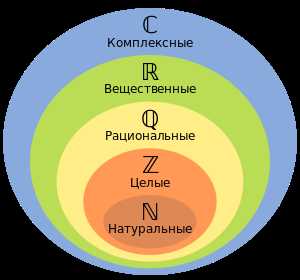
Комплексные числа представляют собой числа вида a + bi, где a и b — действительные числа, а i — мнимая единица, т.е. корень из -1. Они имеют множество применений: от решения уравнений до анализа электрических цепей и основы физических теорий.

Понимание комплексных чисел позволяет нам расширить границы математического мышления и создать новые инструменты для решения различных задач. Это понятие не только полезно в науке и технике, но и открывает новые горизонты для творческого мышления и поиска решений.

Понятие комплексных чисел

Возможно, вы уже задались вопросом: что такое мнимая часть и где она используется в математике? Хорошо, давайте разберемся. Мнимая часть — это число, умноженное на «i«, где «i» — мнимая единица. Мнимая единица определяется как «i = √(-1)». И если вы помните, что извлечение корня из отрицательного числа невозможно в обычной арифметике, то понимаете, что введение мнимой единицы «i» дает нам новые возможности в математике.

Комплексные числа имеют широкое применение в разных областях, как в математике, так и в физике и инженерии. Например, они широко используются в комплексном анализе, электротехнике, теории вероятностей и даже в квантовой механике.

Кроме того, комплексные числа имеют удивительные свойства, которые позволяют решать задачи и проблемы, которые невозможно решить с помощью обычных действительных чисел. Например, комплексные числа позволяют нам решать квадратные уравнения, которые не имеют действительных корней.

Интересно, не правда ли? Ведь на первый взгляд, когда мы учимся математике, кажется, что все числа — это обычные действительные числа. Но комплексные числа расширяют наши возможности и позволяют нам исследовать новые горизонты в математике и других областях знания. Они дают нам способность работать с множеством чисел, включающими в себя действительные и мнимые части.

Так что следующий раз, когда вы увидите комплексное число с мнимой частью, не пугайтесь и не сомневайтесь в его роли и значении. Комплексные числа — это мощный инструмент, который помогает нам лучше понимать и решать сложные математические и физические задачи.

Определение комплексных чисел

Комплексное число обычно записывается в виде z=a+bi, где «a» — действительная часть числа, «b» — мнимая часть числа, и «i» — мнимая единица, которая равна квадратному корню из -1.

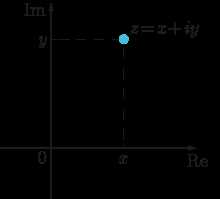
Можно представить комплексное число в виде точки на комплексной плоскости, где действительная часть является абсциссой, а мнимая часть – ординатой. Такая геометрическая интерпретация позволяет наглядно представить операции с комплексными числами.

Комплексные числа имеют множество применений в математике, физике, инженерии и других областях. Они используются для решения уравнений, анализа сигналов, моделирования физических явлений и многого другого. Их использование расширяет возможности и область применения математики.

Разные математики используют разные обозначения для комплексных чисел, но основные свойства и операции с ними универсальны. Определение и применение комплексных чисел обогащает наше понимание чисел и решает проблемы, которые раньше были неразрешимыми. Они представляют собой мощный инструмент для работы с абстрактными и реальными концепциями.

Заключение

Комплексные числа являются неотъемлемой частью математики и имеют широкий спектр применений. Они представляются в виде алгебраической формы и имеют геометрическую интерпретацию на комплексной плоскости. Использование комплексных чисел расширяет наше понимание математики и решает проблемы, которые раньше считались неразрешимыми. Комплексные числа – это не просто абстрактная концепция, а мощный инструмент для решения задач и исследования различных явлений.

Мнимая единица и комплексная единица

Давайте поговорим о двух фундаментальных понятиях в математике: мнимой единице и комплексной единице. Оба этих понятия играют важную роль в различных областях математики, физики и инженерии.

Мнимая единица

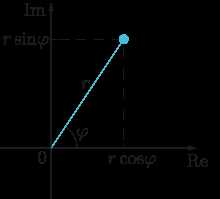
Начнем с мнимой единицы, обозначаемой символом i. Эта величина определяется как квадратный корень из -1. Мнимая единица имеет следующие свойства:

• i * i = -1
• i * —i = 1

Мнимая единица возникает при решении квадратных уравнений, которые имеют отрицательный дискриминант. Хотя мнимые числа не представляют собой физические объекты, они являются мощным инструментом для работы с комплексными числами.

Комплексная единица

Теперь перейдем к комплексной единице, которая обозначается символом j. В отличие от мнимой единицы, комплексная единица является комплексным числом и представляет собой комбинацию вещественной и мнимой частей:

j = 1 + i

Комплексная единица также имеет ряд интересных свойств:

• j * j = -1 + 2i
• j * —j = 1 — 2i

Комплексные числа играют важную роль в математике и физике, особенно в областях, связанных с электричеством, магнетизмом и сигнальной обработкой. Они позволяют удобно представлять и работать с двумерными (или многомерными) векторами, обеими компонентами которых могут быть как вещественные, так и мнимые числа.

Заключение

Таким образом, мнимая единица и комплексная единица являются важными понятиями в математике. Они играют роль в решении различных задач и представляют собой мощные инструменты для работы с комплексными числами. Надеюсь, что эта информация была для вас полезной и позволит вам лучше понять и использовать эти понятия в своей работе.

Применение комплексных чисел

Алгебраические уравнения

Комплексные числа играют важную роль в решении алгебраических уравнений. Некоторые уравнения не имеют решений в области действительных чисел, но могут иметь решения в области комплексных чисел. Например, уравнение $x^2 + 1 = 0$ не имеет решения в области действительных чисел, но имеет два решения в области комплексных чисел: $x = i$ и $x = -i$, где $i$ — мнимая единица.

Электрические цепи

Комплексные числа широко используются в анализе электрических цепей и схем. Они позволяют ученным и инженерам моделировать поведение электрических компонентов и рассчитывать параметры цепей, такие как сопротивление, индуктивность и емкость. Комплексное сопротивление используется для описания понятия импеданса, который зависит от частоты переменного тока.

Теория сигналов

В теории сигналов комплексные числа применяются для анализа и обработки сигналов. Они позволяют представлять сигналы в виде комплексных чисел или комплексных функций, что позволяет решать различные задачи, такие как фильтрация, амплитудная и фазовая модуляция, преобразования Фурье и многое другое.

Квантовая механика

Комплексные числа имеют фундаментальное значение в квантовой механике, которая описывает поведение элементарных частиц и микрообъектов. Волновая функция, которая описывает состояние частицы, является комплексной функцией времени и координаты. Комплексные числа позволяют нам точно описывать и предсказывать результаты экспериментов в квантовой физике.

Геометрия и тригонометрия

Комплексные числа имеют также свое место в геометрии и тригонометрии. Они позволяют нам представить точку на плоскости в виде комплексного числа, а операции сложения, вычитания, умножения и деления комплексных чисел могут быть интерпретированы как геометрические преобразования, такие как повороты и масштабирование.

Геометрическая интерпретация

Одним из способов представления комплексных чисел является комплексная плоскость. На комплексной плоскости комплексное число представляется как точка или вектор, который может быть представлен двумя вещественными числами: действительной и мнимой частью. Действительная часть комплексного числа определяет его расположение на оси X, а мнимая часть определяет его расположение на оси Y.

Комплексная плоскость позволяет нам представить комплексные числа как точки в двумерной геометрической системе. Это дает нам возможность выполнять операции с комплексными числами, такие как сложение и умножение, с помощью геометрических методов.

Например, сложение двух комплексных чисел можно интерпретировать как перемещение по плоскости от одной точки к другой. Умножение комплексных чисел также имеет геометрическую интерпретацию: оно соответствует повороту и масштабированию плоскости.

Геометрическая интерпретация комплексных чисел позволяет нам визуально представить алгебраические операции и понять их свойства. Она также позволяет нам решать геометрические задачи с использованием комплексных чисел, такие как нахождение расстояния между точками или нахождение пересечения прямых.

Геометрическая интерпретация комплексных чисел открывает перед нами новый способ взгляда на математику. Она позволяет нам увидеть связь между числами и геометрией, расширяет наше понимание и помогает нам решать сложные задачи. Использование этой интерпретации может быть весьма полезным и позволит вам лучше понять и применять комплексные числа в различных областях.

Электротехника

Представьте, сколько электронных устройств мы используем каждый день — от мобильных телефонов и компьютеров до бытовой техники и транспортных средств. Все они работают благодаря принципам, изучаемым в электротехнике. Это безусловно сделало нашу жизнь гораздо более удобной и эффективной, но в то же время это создает большую ответственность для профессионалов в этой сфере.

Одной из основных концепций в электротехнике является понятие тока. Ток — это движение электрических зарядов через проводник. Вся электротехника строится на этом принципе. Например, электрические цепи используются для передачи электрической энергии от источника к потребителю. Важно понимать, что электрический ток — это не только поток заряда, но и поток энергии.

Одним из ключевых инструментов в электротехнике являются комплексные числа. Комплексные числа — это числа, состоящие из двух компонентов: действительной и мнимой частей. Они широко используются для моделирования и анализа электрических цепей, так как позволяют учитывать как активную, так и реактивную составляющие электрического тока.

Активная составляющая представляет собой энергию, которая преобразуется в полезную работу, например, освещение или механическое движение. Реактивная составляющая, с другой стороны, является энергией, которая хранится и освобождается в электрической цепи, но не преобразуется непосредственно в полезную работу.

Использование комплексных чисел в электротехнике позволяет более эффективно управлять потоком электроэнергии и учитывать влияние различных параметров, таких как индуктивность и емкость электрических элементов. Это является жизненно важным в условиях современных энергосистем, где энергия должна быть эффективно распределена и сохранена.

Комплексные числа: понятие, применение и значение в математике

Основное значение комплексных чисел заключается в том, что они позволяют решать уравнения с отрицательными дискриминантами. Это особенно важно в алгебре и математическом анализе. Комплексные числа также используются в электротехнике, физике и других научных областях для моделирования и решения сложных задач.

Одно из применений комплексных чисел — это геометрическая интерпретация, где комплексное число представляется в виде точки на плоскости. Действительная часть числа определяет положение по оси X, а мнимая часть — по оси Y. Это позволяет графически представлять операции с комплексными числами, такие как сложение, вычитание, умножение и деление.

Комплексные числа также имеют свои свойства и алгебраические операции, которые позволяют решать уравнения с комплексными корнями. Например, теорема о комплексных корнях гласит, что уравнение n-й степени имеет ровно n корней в комплексных числах.

В целом, комплексные числа являются мощным инструментом в математике и науках, которые позволяют решать разнообразные задачи, связанные с моделированием, решением уравнений, графическим представлением и многими другими областями.