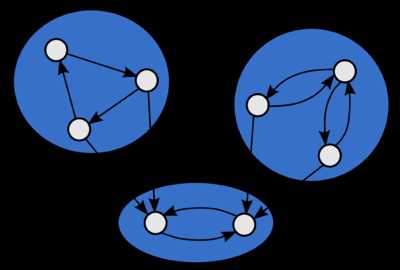
Графы являются важным инструментом для моделирования и анализа различных систем и сетей. Компонент связности графа – это совокупность вершин, которые между собой связаны ребрами, образуя единую подсистему, внутри которой можно достичь любую вершину, двигаясь только по ребрам компонента. Простыми словами, компонент связности графа – это группа вершин, в которой каждая вершина может быть достигнута из любой другой вершины пути.
Определение компонента связности
Когда вы представляете себе граф, вы можете визуализировать компоненты связности, как отдельные «острова», где все вершины внутри каждого острова связаны друг с другом. В то же время, вершины из разных компонентов связности остаются «изолированными» друг от друга.
Для понимания концепции компонента связности можно представить себе группу друзей, где каждый человек представляет вершину, а дружеские связи между людьми — это ребра. Если у нас есть несколько групп друзей, которые не общаются между собой, то каждая группа будет представлять компонент связности.
Основное применение компонента связности в графах заключается в том, что он помогает нам идентифицировать наличие и количество отдельных «частей» в графе. Кроме того, компонент связности может быть использован для анализа связности в различных типах сетей, таких как социальные сети, транспортные сети или сети связи.
Компонент связности имеет большое значение в различных областях исследования, таких как информатика, сетевая теория, теория графов и дискретная математика.
Ориентированный граф
Представьте, что вы планируете сделать путешествие по различным городам. Вы можете использовать ориентированный граф для отображения связей между различными городами. Вершины графа будут представлять города, а ориентированные ребра будут указывать на направление движения от одного города к другому. Это позволит вам наглядно представить маршруты и связи между различными городами.
Ориентированные графы могут также использоваться для моделирования других связей и отношений, таких как связи между компаниями, потоки данных или зависимости между задачами в проекте. Использование ориентированных графов позволяет более точно отобразить направление и характер этих связей.
Для работы с ориентированными графами используются различные алгоритмы и методы, такие как поиск кратчайшего пути, обход графа и определение компонент связности. Эти инструменты помогают анализировать и использовать информацию, содержащуюся в графе, чтобы принимать решения и решать различные задачи.
Неориентированный граф
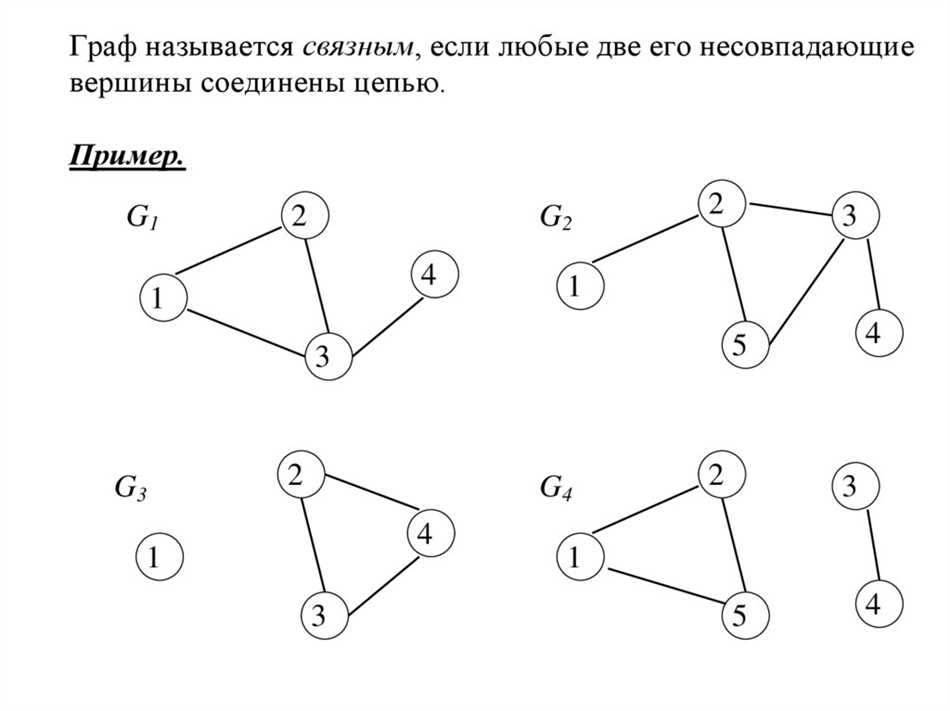
Неориентированный граф — это особый тип графа, в котором отсутствует направление у ребер. Как это понимать? Давай представим, что у нас есть несколько вершин, которые представляют собой точки, и некоторые из этих вершин соединены линиями, которые называются ребрами. В неориентированном графе каждое ребро представляет собой связь между двумя вершинами без указания направления.
Интересно, не правда ли? Ведь в таком графе каждое ребро может рассматриваться как двусторонняя связь. Например, если у нас есть граф, в котором вершины — это города, а ребра — дороги, то неориентированный граф покажет, что между двумя городами есть возможность проехать в обе стороны. Это очень полезно для планирования маршрутов и определения наиболее эффективного пути.
Важно понимать, что в неориентированном графе не существует стрелок, указывающих направление движения. Все вершины и ребра рассматриваются как равноправные, что делает граф более гибким и универсальным для различных задач. Это может быть весьма полезно при изучении социальных сетей, транспортных систем, связи между биологическими объектами и многих других вещей, ведь не всегда можно просто определить однонаправленные связи.
Вот и всё, что я хотел рассказать о неориентированных графах! Надеюсь, тебе стало понятнее, что они такое и как они помогают нам изучать связи и взаимодействия. Если у тебя возникли вопросы, не стесняйся — задавай их и мы вместе найдем на них ответы. Удачи в твоих путешествиях по миру графов!
Пример компоненты связности
Представьте, что вы живете в небольшом городке с четырьмя районами: A, B, C и D. Ваш городок имеет дорожную сеть, соединяющую все эти районы друг с другом. Вы решили изучить компоненты связности в вашем городе.
Вы начинаете свое исследование с района A. От района A вы можете легко добраться до района B, так как существует прямая дорога между ними. Таким образом, районы A и B образуют первую компоненту связности в вашем городе. Вы отмечаете это и продолжаете свое исследование.
Затем вы исследуете районы C и D. К сожалению, между ними нет прямой дороги, поэтому они образуют отдельные компоненты связности. Однако у района C есть дорога, соединяющая его с районом B. Таким образом, район C будет связан с компонентой связности, состоящей из районов A и B.
Итак, в вашем городе есть две компоненты связности. Первая компонента состоит из районов A и B, а вторая компонента — из районов C и D. Эти компоненты связности помогают вам понять, какие районы взаимосвязаны и как они могут быть связаны друг с другом.
Важно отметить, что компоненты связности могут быть любого размера — от двух вершин до всех вершин в графе. Они помогают исследователям понять, какие части графа связаны между собой и как они могут влиять друг на друга.
Алгоритм поиска компонент связности
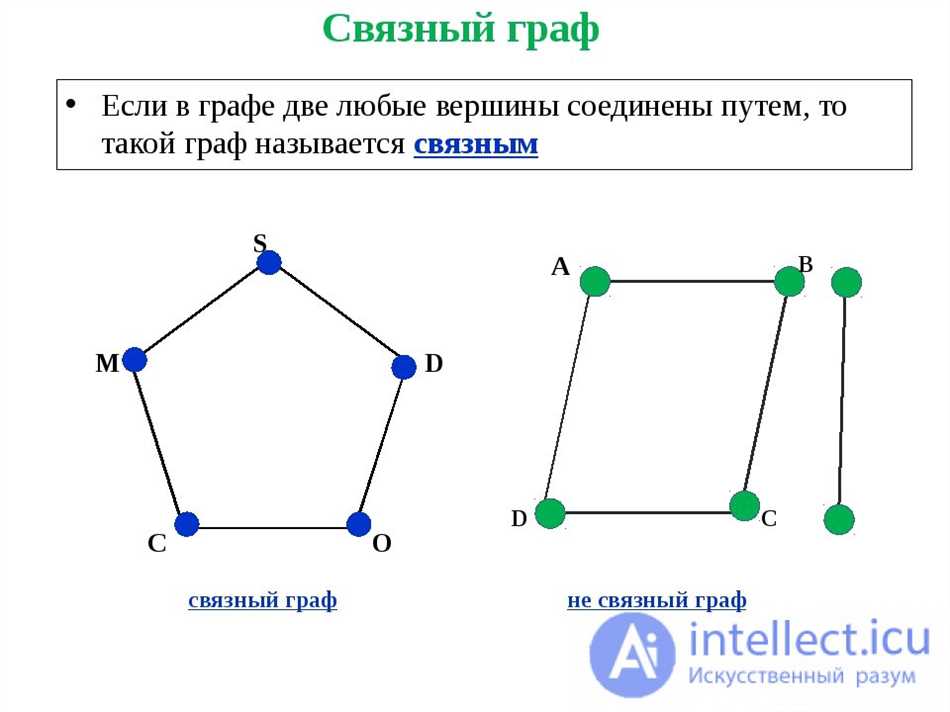
Алгоритм поиска компонент связности основан на идее обхода графа в глубину (DFS). Задача алгоритма — найти все вершины, достижимые из данной и пометить их как часть одной компоненты связности.
Давайте разберемся как это работает на примере. Предположим, у нас есть граф, состоящий из нескольких компонент связности. Наша задача — найти все эти компоненты.
Начнем с выбора любой вершины графа и пометим ее как посещенную. Затем рекурсивно пройдемся по всем соседним вершинам этой вершины, помечая их также как посещенные. Таким образом, мы найдем все вершины, достижимые из текущей вершины.
После этого выберем следующую непосещенную вершину и повторим процесс, пока не посетим все вершины графа. В результате мы получим все компоненты связности, в которых вершины связаны между собой.
Мы можем использовать рекурсивную функцию для реализации данного алгоритма. В начале каждого вызова функции мы будем проверять, посещена ли вершина. Если она уже была помечена, то пропускаем ее. В противном случае, пометим ее как посещенную и проверим все ее соседние вершины.
Алгоритм поиска компонент связности является эффективным и может быть использован для решения различных задач, связанных с графами. Например, он может помочь найти наибольшую компоненту связности в графе или проверить, является ли граф связным.
Таким образом, алгоритм поиска компонент связности является полезным инструментом для работы с графами. Он позволяет нам легко определить, какие вершины связаны между собой, что может быть полезно в различных областях, таких как социальные сети, транспортные сети или анализ данных.
Компонент связности графа: понятие и примеры
Компонент связности графа определяется как максимальное множество вершин, где каждая пара вершин связана маршрутом.
Если в графе каждая вершина связана с другой хотя бы одним путем, то граф называется связным. Если же граф состоит из нескольких связных компонентов, то он является несвязным.
Пример 1:
Рассмотрим граф, состоящий из 6 вершин и 7 ребер:
1-2-3 | / | / | / 4-5-6
В данном примере граф состоит из одной компоненты связности, так как каждая вершина связана с другой хотя бы одним путем.
Пример 2:
Рассмотрим граф, состоящий из 8 вершин и 7 ребер:
1-2-3 / 4-5-6 / 7-8
В данном примере граф состоит из трех компонент связности: {1, 2, 3}, {4, 5, 6} и {7, 8}. В каждой компоненте связности каждая вершина связана с другой хотя бы одним путем, но вершины из разных компонент связности не связаны между собой.
Таким образом, компонент связности графа может быть использован для определения степени связности вершин и обнаружения изолированных компонент графа.



