Компоненты действий в математике: основные понятия и принципы

Математика – это наука, которая включает в себя различные действия и операции. В основе математических вычислений лежат основные понятия и принципы. Знание этих компонентов позволяет нам разбираться в сложных задачах, решать уравнения и прогнозировать результаты. Одним из основных понятий математики является число. Оно может быть целым, рациональным, натуральным или действительным. Еще одним важным компонентом является операция или математическое действие, такое как сложение, вычитание, умножение или деление. Важно знать принципы, которые описывают свойства и законы математических операций. Понимая эти компоненты и принципы, мы можем успешно применять математику в реальной жизни и достигать целей.

Определение компонентов действий

Основными компонентами действий являются:

• Числа: числа являются основными объектами в математике. Они представляют собой количество или меру чего-либо и используются для измерения, сравнения и решения различных математических задач. Числа могут быть целыми, рациональными, иррациональными или комплексными.
• Операции: операции — это действия, которые выполняются над числами и позволяют получить новые числа. Они включают в себя сложение, вычитание, умножение, деление и другие математические операции. Они используются для решения проблем и выполнения вычислений.
• Функции: функции являются особым типом операций, которые принимают одно или несколько входных значений и возвращают выходные значения в соответствии с определенными правилами. Они используются для описания зависимостей между переменными и представляют собой важный инструмент для изучения и моделирования различных явлений.
• Переменные: переменные представляют неизвестные или изменяемые значения в математических выражениях и уравнениях. Они используются для обозначения различных величин и играют ключевую роль в решении проблем и выполнении вычислений.

Комбинирование этих компонентов позволяет нам создавать математические выражения, уравнения и проблемы, и находить их решения. Они помогают нам понять и анализировать различные математические концепции и явления, и дают нам инструменты для решения различных задач в нашей повседневной жизни.

Например, если мы хотим решить задачу о поиске площади прямоугольника, мы будем использовать числа, операции и переменные для вычисления и представления ответа. Математика помогает нам логически мыслить и использовать эти компоненты для решения различных задач и проблем, которые возникают в нашей жизни.

Математическое действие

Математические действия являются основной особенностью математики и служат строительными блоками для решения различных задач. Каждое действие имеет свои правила и свойства, которые позволяют нам выполнять вычисления с точностью и надежностью.

Сложение – это действие, которое объединяет два или более числа для получения их суммы. Оно представляет собой комбинацию или объединение частей, чтобы получить целое. Например, если у тебя есть 3 яблока и 4 яблока, то общее количество яблок будет 7.

Вычитание – это действие, обратное сложению. Оно позволяет нам находить разность между двумя числами. Для выполнения вычитания необходимо отнять одно число от другого. Например, если у тебя есть 7 яблок и ты отдаешь 3 яблока другому человеку, то у тебя останется 4 яблока.

Умножение – это действие, которое объединяет несколько одинаковых групп чисел для получения их общего количества. Оно представляет собой быстрый способ повторного сложения. Например, если у тебя есть 3 ящика, в каждом из которых по 4 яблока, то общее количество яблок будет 12.

Деление – это действие, обратное умножению. Оно позволяет нам разделить одно число на другое для нахождения количества групп или долей. Например, если у тебя есть 12 яблок и ты хочешь разделить их поровну между 3 друзьями, то каждый из них получит по 4 яблока.

Возведение в степень – это действие, которое позволяет нам умножить число на само себя несколько раз. Например, 2 возводится в степень 3 будет равняться 2 × 2 × 2 = 8.

Извлечение корня – это действие, обратное возведению в степень. Оно позволяет нам найти исходное число, которое было возведено в степень. Например, корень квадратный из 9 будет равняться 3, так как 3 × 3 = 9.

Математические действия имеют особые свойства. Например, свойство ассоциативности гласит, что порядок складывания или умножения при выполнении не влияет на результат. Также есть свойство коммутативности, которое означает, что порядок чисел или операций при сложении или умножении не влияет на результат. Эти свойства помогают нам упростить вычисления и позволяют получать одинаковые результаты, не зависимо от порядка чисел или операций.

Математические действия – это основа для решения задач, проведения научных исследований и развития технологий. Они являются неотъемлемой частью нашей повседневной жизни и помогают нам логически мыслить, анализировать информацию и находить решения.

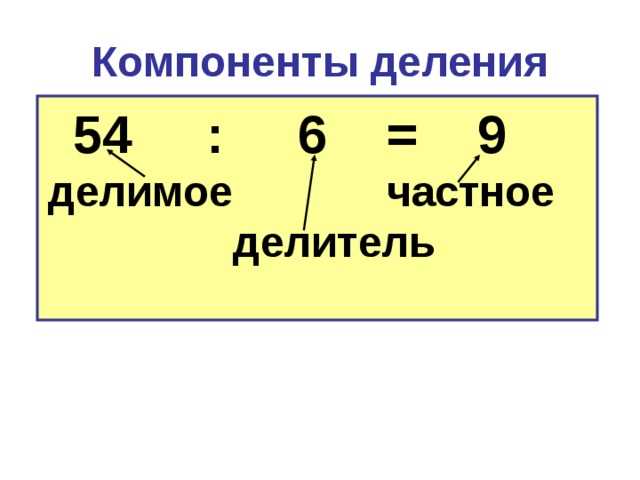
Компоненты математического действия

1. Числа

Одним из основных компонентов математического действия являются числа. Числа используются для измерения, подсчета и сравнения количества объектов. В математике существуют различные типы чисел: натуральные числа, целые числа, рациональные числа, иррациональные числа и действительные числа. Все эти числа позволяют выполнять различные математические операции, такие как сложение, вычитание, умножение и деление.

2. Операторы

Операторы — это символы или знаки, которые обозначают определенные математические операции. Например, плюс (+) обозначает сложение, минус (-) — вычитание, умножение (*) — умножение, деление (/) — деление. Операторы позволяют сочетать числа и выполнять над ними нужные нам действия.

3. Порядок операций

Порядок операций играет важную роль в математике. Он определяет последовательность выполнения операций при выполнении сложных выражений. Правильное применение порядка операций позволяет получить правильный результат. Классическим примером порядка операций является умножение и деление, выполняемые перед сложением и вычитанием.

4. Скобки

Скобки — это специальные символы, которые используются для группировки операций в математических выражениях. С помощью скобок можно указать, какие операции нужно выполнить в первую очередь. Например, в выражении (2 + 3) * 4 сначала выполняется операция в скобках, а затем умножение.

5. Переменные

Переменные — это символы или буквы, которые представляют неизвестные значения или значения, которые могут изменяться. Они используются для обозначения неизвестных или переменных в уравнениях и выражениях. Например, в уравнении x + 5 = 10 переменная x обозначает неизвестное число, которое нужно найти.

6. Функции

Функции — это особые математические выражения, которые принимают одно или несколько значений и возвращают результат. Они позволяют нам выполнять сложные математические операции и преобразования. Примерами функций могут быть функция сложения (sum), функция умножения (multiply) и функция возведения в степень (power).

Все эти компоненты математического действия взаимодействуют между собой и позволяют нам решать сложные математические задачи, а также применять математику в повседневной жизни. Знание и понимание этих компонентов помогает нам стать лучше в анализе, решении проблем, аргументации и критическом мышлении. Математика — это нечто большее, чем просто набор чисел и операций, она развивает нас как логически мыслящих людей и помогает нам решать сложные задачи в различных областях нашей жизни.

Базовые действия

Основные базовые действия математики включают в себя сложение, вычитание, умножение и деление. Сложение – это процесс объединения двух или более чисел для получения суммы. Например, если у вас есть 2 яблока и вы добавляете еще 3 яблока, то в результате у вас будет 5 яблок. Вычитание, напротив, представляет собой процесс удаления одного числа из другого. Например, если у вас есть 5 яблок и вы съедаете 2, то у вас останется 3 яблока.

Умножение – это процесс, при котором одно число увеличивается на множитель другого числа. Например, если у вас есть 3 группы по 4 яблока в каждой, то общее количество яблок будет равно 12. Деление, напротив, представляет собой противоположную операцию, при которой число делится на множитель, чтобы получить исходное число. Например, если у вас есть 12 яблок и вы раздаете их на 3 группы, то в каждой группе будет по 4 яблока.

Базовые действия позволяют нам решать различные математические проблемы, а также решать повседневные задачи, связанные с финансами, измерениями и другими ситуациями. Например, при покупке товаров в магазине мы используем умножение для рассчета общей стоимости покупки, а при дележе счета в ресторане мы используем деление для распределения оплаты между участниками. Без знания базовых действий нам было бы гораздо сложнее справиться с такими ситуациями.

Понимание базовых действий также дает нам возможность лучше понять и использовать различные математические концепции, такие как алгебра и геометрия. Они являются строительными блоками для более сложных математических операций и понятий.

Таким образом, базовые действия являются неотъемлемой частью нашей жизни и знание их позволяет нам решать различные задачи и проблемы более эффективно и уверенно. Не стоит недооценивать их значимость и необходимость в повседневной жизни.

Взаимодействие компонентов действий

Когда мы решаем математическую задачу или выполняем какое-либо действие, мы не просто применяем некоторые алгоритмы или формулы. Вместо этого мы взаимодействуем с различными компонентами действий, которые вместе образуют процесс решения задачи. Эти компоненты взаимодействуют между собой, взаимодействуют с нашим мышлением и судьбой. Это взаимодействие определяет наш успех или неудачу в решении задачи.

Одним из ключевых компонентов действий является понимание математических концепций и принципов. Если мы не понимаем, как работает определенная формула или как применять определенное правило, то мы не сможем использовать их в наших вычислениях. Поэтому важно обратить особое внимание на понимание математических концепций и принципов и уделить время и усилия на их изучение и усвоение.

Следующий компонент действий — это навыки решения задач. Чем больше мы практикуемся в решении различных задач, тем лучше мы становимся в этом. Навыки решения задач позволяют нам быстро ориентироваться в сложных ситуациях, видеть неочевидные решения и эффективно использовать наши знания и умения.

Кроме того, эмоциональное состояние играет важную роль в процессе решения математических задач. Если мы испытываем стресс, страх или негативные эмоции, это может оказать отрицательное влияние на наше мышление и работу с задачей. Поэтому важно научиться управлять своими эмоциями и создавать подходящую атмосферу для успешного решения задач.

Наконец, последний компонент действий — это мотивация и уверенность в себе. Если мы не верим в свои способности или не видим смысла в решении задачи, то мы не сможем осуществить свои замыслы. Мотивация помогает нам преодолеть трудности и находить внутренние резервы для решения задачи.

Таким образом, взаимодействие компонентов действий играет важную роль в процессе решения математических задач. Используя правильное понимание концепций и принципов, развивая логическое мышление, улучшая навыки решения задач, управляя эмоциями и повышая уверенность в себе, мы можем достичь успеха в математике и в других областях жизни. Вы готовы использовать эти компоненты для достижения своих целей?

Принципы компонентов действий

Когда мы говорим о компонентах действий в математике, имеется в виду система основных принципов, которые помогают нам понять и усвоить различные аспекты математических операций. Эти принципы представляют собой основу для выполнения сложных действий и оказываются полезными во множестве математических областей.

Первый принцип компонентов действий — это принцип построения действий. Он заключается в том, что каждое действие в математике можно разбить на более мелкие компоненты или шаги. Например, сложение чисел можно разбить на несколько шагов: 1) записать числа одно под другим; 2) сложить единицы; 3) сложить десятки и т.д. Такой подход позволяет нам лучше понять и выполнить сложные математические операции.

Второй принцип компонентов действий — это принцип соединения действий. Он гласит, что каждый шаг или компонент действия должен быть логически связан с предыдущими шагами. В математике необходимо учитывать последовательность выполнения действий, чтобы получить верный результат. Например, если мы захотим выполнить операцию «сложение», но сначала выполним вычитание, то результат будет неверным.

Третий принцип компонентов действий — это принцип обратной связи. Он заключается в том, что после выполнения каждого шага необходимо проверять его результат и сравнивать его с ожидаемым результатом. Если результат не соответствует ожиданиям, то нужно вернуться к предыдущим шагам и исправить ошибку. Этот принцип помогает нам быть более внимательными и точными при выполнении действий.

Четвертый принцип компонентов действий — это принцип оценки действий. Он гласит, что каждое действие должно быть оценено после выполнения. Мы должны задавать себе вопросы, такие как: Верно ли я выполнил каждый шаг? Верный ли был результат? Могу ли я найти другой путь к решению? Этот принцип позволяет нам развить критическое и аналитическое мышление, а также улучшить наши навыки в решении задач.

Компоненты действий в математике: основные понятия и принципы

Основные понятия в математике определяют базовую систему, на основе которой производятся все вычисления и операции. Основные понятия включают в себя такие элементы, как числа, операции, функции, уравнения, пропорции и т. д. Эти понятия являются основой для построения более сложных компонентов.

Принципы в математике представляют собой общие правила и законы, которые используются при выполнении действий. Принципы включают в себя такие правила, как коммутативность, ассоциативность, дистрибутивность и т. д. Эти принципы позволяют выполнить действия более эффективно и точно.

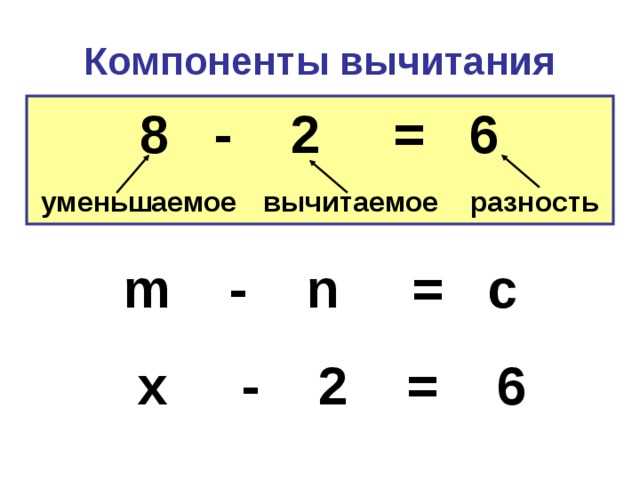
Компоненты действий в математике – это элементы, которые применяются для выполнения конкретных действий, таких как сложение, вычитание, умножение и деление. Компоненты действий могут быть представлены в виде таблиц или списков, где для каждого действия указывается его определение, свойства и особенности.

Например, для операции сложения основными компонентами являются слагаемые и сумма. Слагаемые – это числа, которые складываются, а сумма – результат сложения. Для каждого компонента могут быть указаны его свойства, например, коммутативность (порядок слагаемых не влияет на сумму) и ассоциативность (порядок складывания не влияет на сумму).

Таким образом, компоненты действий в математике являются основными элементами, на основе которых строятся все вычисления и операции. Понимание и использование этих компонентов позволяет выполнять действия более эффективно и точно.