Математические действия – это основные операции, которые мы используем в повседневной жизни, чтобы решать различные задачи. Они состоят из различных компонентов, которые помогают нам понять и выполнять эти действия. Важно знать основные компоненты математических действий, чтобы правильно решать задачи и применять их в реальной жизни. Например, при выполнении сложения – одного из математических действий – используются понятия слагаемых и суммы. Понимая и применяя эти компоненты, мы можем легко и точно выполнять математические действия.
- Понятие компонентов математических действий
- Определение компонентов математических действий
- Значение компонентов математических действий
- Основные компоненты математических действий
- 1. Числа
- 2. Операции
- 3. Знаки и символы
- 4. Приоритеты и правила
- 5. Примеры
- Сложение
- Вычитание
- Умножение
- Компоненты математических действий: понятие и примеры
- 1. Числа
- 2. Операторы
- 3. Индексы и степени
- 4. Скобки
- 5. Предикаты и условия
- 6. Переменные
- 7. Функции
- 8. Равенства и неравенства
Понятие компонентов математических действий
Компоненты математических действий — это ключевые элементы, которые составляют основу математического мышления и позволяют нам выполнять различные вычисления. Они включают в себя:
- Числа: числа являются основой математических действий. Они представляют собой символы, которыми мы обозначаем количество или величину. Числа могут быть целыми, десятичными, рациональными или иррациональными. Вся математика, в конечном счете, сводится к манипуляции с числами.
- Операции: операции – это математические действия, которые выполняются с числами, чтобы получить новое число или результат. Они включают в себя сложение, вычитание, умножение и деление. Операции могут быть как простыми, так и сложными, и часто сочетаются друг с другом в более сложные выражения или уравнения.
- Функции: функции – это особые математические выражения, которые связывают одно число с другим или одну величину с другой. Они, по сути, описывают зависимость между двумя или более переменными, и могут быть использованы для моделирования различных процессов и явлений в науке, экономике и других областях.
- Знаки и символы: знаки и символы играют важную роль в математических действиях. Они помогают нам представить операции, отношения или связи между числами и величинами. Например, знаки «+», «-«, «*», «/» обозначают соответственно сложение, вычитание, умножение и деление.
Понимание и использование этих компонентов является основой успешного выполнения математических задач. Они помогают нам анализировать, сравнивать, вычислять и представлять различные математические величины и отношения.
Теперь представьте себе, что вы выполняете математические действия без знания чисел, операций, функций и знаков. Как бы вы решали задачи, делали вычисления или принимали решения, касающиеся математической информации? Проблема была бы значительно усложнена и понимание математики стало бы невозможным.
Итак, понимание и использование компонентов математических действий – это ключевые навыки, которые помогают нам успешно работать с числами и вычислениями в разных ситуациях. Они позволяют нам увидеть мир через призму чисел и операций, раскрывая перед нами новые возможности и перспективы.
Определение компонентов математических действий
Компоненты математических действий — это различные элементы, которые входят в состав каждого математического действия. Они являются строительными блоками, с помощью которых мы решаем математические задачи и выполняем операции. Каждый компонент выполняет свою роль и взаимодействует с другими компонентами, образуя полное математическое действие.
Основные компоненты математических действий:
- Числа: числа являются основой всех математических действий. Они представляют количество и используются для измерения и вычислений. Числа можно складывать, вычитать, умножать и делить друг на друга.
- Операции: операции — это действия, которые мы выполняем с числами. Операции включают сложение, вычитание, умножение и деление. Они позволяют нам изменять и манипулировать числами.
- Знаки: знаки в математике используются для обозначения операций. Знак плюс (+) обозначает сложение, знак минус (-) — вычитание, знак умножения (×) — умножение, знак деления (÷) — деление.
- Приоритеты: приоритеты определяют порядок выполнения математических операций. Существует определенная иерархия, которую нужно учитывать при выполнении нескольких операций в одном выражении.
Для того чтобы успешно решать математические задачи, необходимо понимать и уметь применять все компоненты математических действий. Числа и операции являются стандартными элементами каждого математического выражения, их знание и умение правильно использовать позволяют достичь правильного решения. Знание знаков и приоритетов также является важным, так как они определяют порядок действий и обеспечивают точность вычислений.
Теперь, когда вы понимаете, что такое компоненты математических действий, вы можете смело приступать к решению математических задач и операций. Знание этих компонентов поможет вам разобраться в любых числовых вопросах и найти правильное решение. Успехов в ваших математических приключениях!
Значение компонентов математических действий
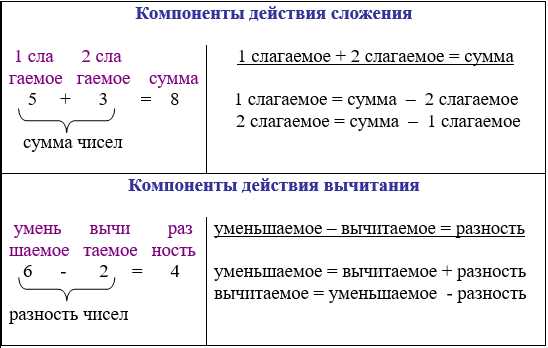
Сложение — это действие, при котором мы объединяем два или более числа, чтобы получить их сумму. Оно может быть применено к любым числам, положительным или отрицательным. Например, если у нас есть два числа: 3 и 5, то их сумма будет равна 8.
Вычитание — это действие, обратное сложению. Оно используется для нахождения разности между двумя числами. Вычитание можно воспринимать как «изъятие» одного числа из другого. Например, если у нас есть число 10 и мы вычитаем из него число 3, то разность будет равна 7.
Умножение — это действие, при котором мы увеличиваем значение одного числа на значение другого числа. Оно используется для быстрого сложения одинаковых чисел и для нахождения общего количества элементов в группе. Например, если у нас есть 3 группы по 4 яблока в каждой, то общее количество яблок будет равно 12.
Деление — это действие, обратное умножению. Оно используется для разделения одного числа на другое. Деление позволяет нам найти количество равных частей, на которые мы можем разделить число. Например, если у нас есть число 12 и мы делим его на 3, то результатом будет число 4, так как 12 делится на 3 без остатка на 4 равные части.
Знание и понимание компонентов математических действий позволяет нам решать сложные математические задачи, делать точные вычисления и применять математику в повседневной жизни. Умение применять эти действия при решении проблем помогает развивать логическое мышление, аналитические навыки и уверенность в своих математических способностях.
Основные компоненты математических действий
Основными компонентами математических действий являются:
1. Числа
Числа – это базовые элементы математики. Они представляют собой количество или количество чего-то. Мы используем числа для измерения, подсчета и сравнения. Числа могут быть натуральными (1, 2, 3…), целыми (-2, -1, 0, 1, 2…), рациональными (дроби) и иррациональными (например, пи). Каждое число имеет свои особенности и свойства, которые помогают нам выполнять различные математические действия.
2. Операции
Операции – это способы комбинирования чисел для получения новых результатов. Основными операциями являются сложение, вычитание, умножение и деление. Кроме того, есть и другие операции, такие как возведение в степень, извлечение корня, деление с остатком и т.д. Каждая операция имеет свои правила и свойства, которые помогают нам совершать математические действия точно и эффективно.
3. Знаки и символы

Знаки и символы – это специальные обозначения, которые используются для записи и обработки математической информации. Мы используем знаки плюс (+), минус (-), умножить (×), разделить (÷) и равно (=) для обозначения операций и связывания чисел. Кроме того, существуют знаки для больше (>) и меньше (<), а также знаки для выражения отношений, пропорций и других математических концепций. Правильное использование знаков и символов позволяет нам четко выражать математические идеи и общаться друг с другом на языке математики.
4. Приоритеты и правила
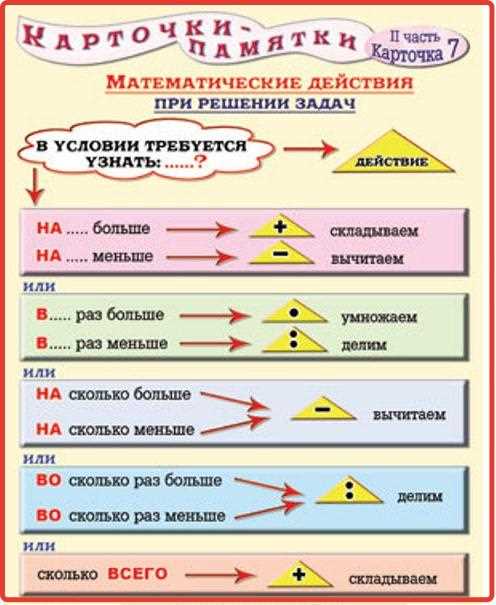
Приоритеты и правила – это наборы правил, которые определяют порядок выполнения математических действий. Например, сначала выполняются операции в скобках, а затем умножение и деление перед сложением и вычитанием. Знание правил и приоритетов помогает нам совершать математические действия последовательно и правильно. Это также позволяет избежать путаницы и получить точные результаты.
5. Примеры
Примеры математических действий охватывают широкий спектр ситуаций, начиная с простых расчетов и заканчивая сложными алгоритмами. Например, сложение 2 и 3 дает результат 5, а умножение 4 на 8 дает результат 32. Более сложные примеры могут включать решение уравнений, нахождение процентов, решение задач по геометрии и многое другое. Примеры помогают нам увидеть, как применяются основные компоненты математических действий в реальной жизни и как мы можем использовать их для решения различных задач.
Итак, основными компонентами математических действий являются числа, операции, знаки и символы, приоритеты и правила. Понимание и применение этих компонентов позволяет нам улучшить наши математические навыки и использовать их для решения различных задач в нашей повседневной жизни.
Сложение

Когда мы складываем, мы объединяем две или более группы вместе, чтобы получить единую группу. Например, если у тебя есть 2 яблока и твой друг дает тебе еще 3 яблока, то складывая их вместе, мы получим общее количество яблок, равное 5.
Сложение мы обозначаем с помощью символа «+». Например, если мы хотим сложить 2 и 3, мы пишем «2 + 3». Результатом сложения будет число, равное 5.
Сложение можно использовать не только для чисел, но и для других величин. Например, мы можем сложить две строки текста, объединив их в одну строку. Также мы можем сложить два множества предметов, соединив их в одно большое множество.
Сложение имеет несколько свойств, которые помогают нам упростить вычисления и понять его правила.
- Сложение коммутативно – это значит, что порядок слагаемых не имеет значения. Например, 2 + 3 равно 3 + 2.
- Сложение ассоциативно – это значит, что сумма не изменяется, если поменять местами складываемые числа или изменить их порядок. Например, (2 + 3) + 4 равно 2 + (3 + 4), и оба выражения равны 9.
Сложение имеет много применений в нашей жизни. Мы используем его для подсчета денег, суммирования оценок по предметам, определения общего времени, затраченного на выполнение задачи, и многое другое.
Так что не бойся сложения и используй его для упрощения своих задач и повседневных ситуаций! Надеюсь, теперь тебе стало понятно, что такое сложение и как его применять.
Вычитание
Суть вычитания очень проста: мы берем первое число, которое называется уменьшаемым, и из него вычитаем второе число, которое называется вычитаемым. Результат вычитания называется разностью.
Давайте рассмотрим пример. У вас было 10 яблок, но вы съели 3 яблока. Сколько яблок осталось? Чтобы найти ответ, мы вычитаем количество съеденных яблок (вычитаемое) из изначального количества яблок (уменьшаемого). В данном случае, 10 — 3 = 7, поэтому у вас осталось 7 яблок.
Вычитание используется повсюду: в школе, в работе, в повседневной жизни. Например, когда вы считаете сдачу в магазине или вычитаете количество отработанных дней со своего отпуска, вы применяете операцию вычитания. Вычитание также является важным компонентом более сложных математических операций, таких как деление и умножение.
Важно помнить, что порядок вычитания может влиять на результат. Например, 5 — 3 = 2, но 3 — 5 = -2. В первом случае мы уменьшаем 5 на 3 и получаем положительный результат. Во втором случае мы пытаемся вычесть большее число из меньшего, что приводит к отрицательному результату.
Также следует отметить, что вычитание может иметь разные способы записи. Вместо символа «-«, мы также можем использовать слова «минус» или «от». Например, 7 — 2 можно записать как «7 минус 2» или «7 от 2». Все эти выражения означают одно и то же — вычитание.
Вычитание — это важный инструмент в математике и в жизни в целом. Оно помогает нам решать задачи, принимать решения и понимать окружающий мир. Практика вычитания поможет вам развить навыки анализа и логического мышления. Не бойтесь использовать его и никогда не переставайте исследовать мир вокруг с помощью математики!
Умножение
Операция умножения может применяться в самых разных ситуациях в нашей повседневной жизни. Например, при покупке продуктов в магазине мы можем умножить стоимость одного товара на его количество, чтобы узнать общую сумму покупки. Также умножение может помочь нам решать задачи в финансах, строительстве, науке и многих других областях.
Основное правило умножения состоит в том, что произведение двух чисел равно сумме их одинаковых слагаемых. Например, 3 * 4 = 12. В этом примере мы умножаем число 3 на число 4, и получаем сумму 12 одинаковых слагаемых, равных 3.
Умножение можно представить как повторение одного и того же числа несколько раз. Например, 5 * 2 можно представить как 5 + 5, что равно 10.
Когда мы умножаем число на 0, результат всегда будет равен 0. Например, 7 * 0 = 0. Это связано с тем, что умножение на 0 означает отсутствие объектов или действий.
В математике умножение можно представить в виде таблицы умножения, которая помогает запомнить основные результаты умножений от 1 до 10. Таблица умножения также помогает ученикам развить навыки умножения и быстро находить произведения чисел.
Например, таблица умножения:
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Запомни таблицу умножения, и у тебя всегда будет под рукой быстрый способ выполнить умножение!
Компоненты математических действий: понятие и примеры
1. Числа
Числа — это основные компоненты, с которыми проводятся математические действия. Они могут быть целыми, дробными, положительными, отрицательными и т.д. Примеры чисел: 5, -3.14, 1/2.
2. Операторы
Операторы определяют тип математического действия и указывают, что нужно сделать с числами. Они могут быть арифметическими (сложение, вычитание и т.д.), логическими (и, или, не) или другими. Примеры операторов: +, -, *, /.
3. Индексы и степени
Индексы и степени указывают на количество повторений числа или на его позицию в степени. Используются для обозначения корней, факториалов и других математических конструкций. Примеры: √2, 52 (5 в квадрате).
4. Скобки
Скобки используются для определения порядка выполнения математического действия и для изменения его значения. Они могут быть круглыми, квадратными или фигурными. Примеры: (2 + 3) * 4, 2 / (3 + 1).
5. Предикаты и условия
Предикаты и условия используются для определения, выполняется ли какое-либо условие или истинно ли какое-либо утверждение. Они используются в логических операциях. Примеры: 2 > 1 (утверждение истинно), 5 < 3 (утверждение ложно).
6. Переменные
Переменные — это символы, которые обозначают неизвестные или изменяющиеся значения. Они позволяют создавать универсальные формулы и решать уравнения. Пример: x + 5 = 10.
7. Функции
Функции — это специальные математические операции, которые принимают одно или несколько чисел и возвращают результат. Они могут быть простыми (синус, косинус и т.д.) или сложными (логарифм, экспонента и др.). Примеры: sin(30°), log2(8).
8. Равенства и неравенства
Равенства и неравенства используются для сравнения двух чисел или выражений и определения их отношения. Они могут быть равными (=), больше (>), меньше (<) и т.д. Примеры: 2 + 3 = 5, 4 > 2.