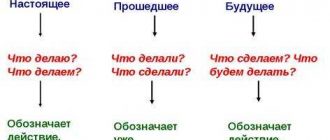
Компоненты сложения и вычитания – это числа, которые объединяются вместе, чтобы найти сумму или разность. Когда мы складываем два числа, они называются слагаемыми. Первое слагаемое и второе слагаемое – они составляют сложение. Аналогично, когда мы вычитаем одно число из другого, первое число называется уменьшаемым, а второе – вычитаемым.
Знание компонентов сложения и вычитания особенно полезно при решении задач: при постановке задачи нам необходимо определить, какие числа являются слагаемыми, а какие являются уменьшаемым и вычитаемым. Уверен, что после прочтения этой статьи ты сможешь легко разобраться в этих понятиях и успешно применять их в своих математических решениях!
- Основные понятия сложения и вычитания
- Сложение
- Вычитание
- Числа
- Целые числа
- Дробные числа
- Сложение
- Свойства сложения
- Свойство коммутативности
- Свойство ассоциативности
- Свойство нейтрального элемента
- Порядок сложения
- Коммутативное свойство
- Ассоциативное свойство
- Вычитание
- Компоненты сложения и вычитания: основные понятия и применение
Основные понятия сложения и вычитания
Сложение
Сложение — это процесс объединения двух или более чисел, чтобы получить их сумму. Все числа, которые мы складываем, называются слагаемыми. Результат сложения называется суммой.
Например, если у нас есть два числа 5 и 3, мы можем их сложить:
5 + 3 = 8
В этом примере числа 5 и 3 являются слагаемыми, а число 8 — суммой. Мы можем представить сложение в виде геометрической модели с помощью числовой линии или числовой плоскости. На числовой линии мы начинаем с первого числа и двигаемся вправо на расстояние, равное второму числу, чтобы получить сумму.
Вычитание
Вычитание — это процесс нахождения разности двух чисел. Одно число называется уменьшаемым, а другое — вычитаемым. Результат вычитания называется разностью.
Например, если у нас есть два числа 8 и 3, мы можем их вычесть:
8 — 3 = 5
В этом примере число 8 является уменьшаемым, а число 3 — вычитаемым. Число 5 — разностью. Мы можем представить вычитание также с помощью числовой линии или числовой плоскости. На числовой линии мы начинаем с первого числа и двигаемся влево на расстояние, равное второму числу, чтобы получить разность.
Сложение и вычитание являются важными навыками, которые помогают нам в повседневной жизни. Мы можем использовать их для подсчета денег, объема продуктов, времени и многих других вещей. Эти операции также являются основой для других математических концепций, таких как умножение и деление.
Теперь, когда мы знаем основные понятия сложения и вычитания, давайте потренируемся в их применении и станем мастерами арифметики!
Числа
Числа могут быть разделены на различные категории, такие как натуральные числа, целые числа, рациональные числа и действительные числа. Натуральные числа — это положительные целые числа, которые мы используем для подсчета объектов. Например, если у нас есть три яблока, мы можем представить это числом 3. Целые числа включают в себя натуральные числа, ноль и отрицательные числа. Рациональные числа могут быть представлены как отношение двух целых чисел, например, 1/2 или 3/4. Действительные числа включают в себя все рациональные числа, а также иррациональные числа, такие как корень из 2 или число π.
В нашей повседневной жизни мы используем числа для решения различных задач. Мы считаем деньги, измеряем длину или массу предметов, вычисляем время или рассчитываем скорость движения. Числа также широко используются в физических и научных расчетах, а также в программировании и компьютерных науках.
Числа могут иметь различные свойства и взаимоотношения. Они могут быть складываться, вычитаться, умножаться или делиться друг на друга. Компоненты сложения и вычитания — основные математические операции, которые позволяют нам соединять и разделять числа для решения задач и получения новых числовых значений. Например, если у нас есть число 5 и мы прибавляем к нему число 3, мы получаем сумму 8. Если у нас есть число 5 и мы вычитаем из него число 3, мы получаем разность 2.
Математика и числа — это увлекательная и практическая область знаний, которая помогает нам понимать и описывать мир вокруг нас. Она дает нам возможность решать задачи и находить креативные решения. Узнайте больше о числах и их применении, и расширьте свои знания в этой увлекательной области! Не переживайте, математика может быть интересной и веселой! Время начать увлекательное математическое путешествие в мир чисел!
Целые числа

Целые числа могут быть положительными, отрицательными или нулем, и они могут быть представлены на числовой прямой. Когда мы складываем два целых числа, мы можем перемещаться вправо или влево по числовой прямой, в зависимости от знака каждого числа.
Если мы складываем положительное число с положительным числом, мы движемся вправо на числовой прямой и получаем положительное число в качестве результата. Например, 3 + 2 = 5.
Если мы складываем отрицательное число с отрицательным числом, мы движемся влево на числовой прямой и получаем отрицательное число в качестве результата. Например, -3 + (-2) = -5.
Если мы складываем положительное число с отрицательным числом, то это похоже на движение вправо и влево одновременно на числовой прямой. Если положительное число больше по абсолютной величине, чем отрицательное число, мы движемся вправо и получаем положительное число в качестве результата. Например, 5 + (-3) = 2. Если же отрицательное число больше по абсолютной величине, чем положительное число, мы движемся влево и получаем отрицательное число в качестве результата. Например, 3 + (-5) = -2.
Вычитание целых чисел работает аналогичным образом. Когда мы вычитаем одно целое число из другого, мы двигаемся вправо или влево на числовой прямой, в зависимости от знака каждого числа. Если мы вычитаем положительное число из положительного числа, мы движемся влево и получаем положительное число в качестве результата. Например, 5 — 3 = 2.
Задачи с применением целых чисел могут быть интересными и вызовут интерес. Какие бы хуеты мы ни делали со сложением и вычитанием целых чисел, их конечный результат всегда будет целым числом. Это даёт нам уверенность в правильности наших вычислений и позволяет получать точные ответы. Так что не бойся сложных задач и попробуй твои навыки с целыми числами!
Дробные числа
Представьте, что вы идете в магазин и хотите купить полкило яблок. Чтобы точно указать, сколько яблок вы хотите купить, вам нужно будет указать число яблок в виде десятичной дроби, например 0,5. Здесь 0 — это целая часть числа, а 5 — это дробная часть числа, которая указывает, что вы хотите половину килограмма яблок.
Очевидно, что дробные числа пригождаются не только в покупках. Например, они используются в кулинарии при приготовлении рецептов, так как точно указывают, сколько ингредиентов требуется добавить. Или, представьте себе строителя, который должен построить стену определенной длины — он должен измерить, насколько длинной нужно сделать каждую часть стены, чтобы она была точно такой, какую задумал архитектор.
Дробные числа также находят свое применение в финансовой сфере. Например, они используются для вычисления процентов, расчета торговой наценки или определения доли прибыли в процентах.
Также дробные числа неотъемлемо присутствуют в математике, где используются как часть операций сложения, вычитания, умножения и деления. Все эти операции могут быть выполнены с дробными числами точно так же, как и с целыми числами, но требуют дополнительных правил и навыков.
Например, при сложении или вычитании дробей требуется иметь общий знаменатель, чтобы произвести правильные вычисления. Также важно помнить, что после выполнения операции сложения или вычитания дроби могут быть приведены к несократимому виду.
Важно понимать, что дробные числа не всегда представляются в виде десятичных дробей. Они могут быть представлены и в виде обыкновенных дробей, когда числитель и знаменатель являются целыми числами.
Дробные числа являются важным инструментом для точных измерений и вычислений, их применение распространено во многих сферах нашей жизни. Понимание основных понятий о дробных числах поможет нам справиться с повседневными задачами на работе, в школе или дома.
Сложение
Результатом сложения двух или более чисел является их сумма. Сложение можно представить как объединение двух групп объектов или как перемещение по числовой оси вправо.
Допустим, у нас есть 3 яблока и мы добавляем к ним еще 2 яблока. Сколько у нас будет яблок всего? Мы можем использовать сложение, чтобы найти ответ: 3 + 2 = 5. Таким образом, у нас будет 5 яблок в сумме.
В математике есть специальные символы, которые используются для обозначения сложения. Знак плюс (+) используется для обозначения операции сложения. Например, 3 + 2 = 5. Здесь 3 и 2 — слагаемые, а 5 — сумма.
Сложение может быть свободным или связанным с определенными правилами. Например, мы можем сложить числа в любом порядке, и результат будет одинаковым. 3 + 2 и 2 + 3 дадут одинаковый результат — 5.
Сложение также работает с отрицательными числами. Если есть отрицательное число, мы можем считать его как уменьшение. Например, 5 + (-3) = 2. Здесь мы добавляем 5, а затем вычитаем 3, что дает нам 2.
Сложение имеет много практических применений в нашей повседневной жизни. Мы используем его для счета денег, подсчета времени, подсчета символов в тексте и многих других вещей. Понимание сложения помогает нам быть более организованными и уверенными в наших математических навыках.
Свойства сложения
Свойство коммутативности
Первое свойство сложения — коммутативность. Это означает, что порядок слагаемых не влияет на результат. Например, 2 + 3 будет равно 3 + 2. Попробуйте проверить это на практике: сложите эти два числа в любом порядке и убедитесь, что итоговая сумма остается неизменной. Коммутативность сложения очень удобна, потому что позволяет нам менять местами числа и сокращать вычисления.
Свойство ассоциативности
Следующее свойство сложения — ассоциативность. Простыми словами, оно означает, что группировка слагаемых не влияет на итоговую сумму. Например, (2 + 3) + 4 будет равно 2 + (3 + 4). Попробуйте провести эти вычисления и убедитесь, что в обоих случаях результат будет один и тот же. Ассоциативность сложения помогает нам упрощать сложные выражения и сокращать количество операций.
Свойство нейтрального элемента
Еще одно важное свойство сложения — наличие нейтрального элемента. Это число, которое при сложении с любым другим числом не меняет его. В случае сложения это число 0. Например, 5 + 0 будет равно 5. Попробуйте сложить любое число с 0 и убедитесь, что результат не изменится. Наличие нейтрального элемента делает сложение удобным и позволяет нам легко выполнять вычисления.
Ответьте себе на вопрос: как эти свойства сложения помогают нам в повседневной жизни? Может быть, вы когда-нибудь меняли порядок слагаемых при подсчете расходов или группировали слагаемые, чтобы упростить вычисления? Подумайте и найдите примеры из своего опыта, которые показывают применение этих свойств сложения в реальной жизни.
Нейтральный элемент сложения, свойство коммутативности и ассоциативности – удивительные и полезные свойства, которые помогают нам понять и применять сложение. Используйте их в своих вычислениях и наслаждайтесь удобством и простотой математики.
Порядок сложения
Вы когда-нибудь задумывались о том, как происходит сложение чисел? Почему мы складываем именно в определенном порядке? Давайте разберемся вместе!
Когда мы складываем два или более числа, сначала мы смотрим на их значения и решаем, какой порядок сложения будет лучше использовать. Ведь порядок сложения может повлиять на результат!
Коммутативное свойство
В математике есть одно замечательное свойство, называемое коммутативным свойством. Оно гласит, что порядок слагаемых не влияет на результат сложения. Другими словами, результат будет одинаковым, независимо от того, какой порядок мы выберем.
Например, если мы сложим числа 2 и 3, не имеет значения, сначала ли мы прибавим 2 к 3 или 3 к 2. В обоих случаях мы получим ответ 5. Это свойство очень удобно при сложении чисел, так как оно позволяет нам более гибко менять порядок и хранить числа в удобном для нас формате.
Ассоциативное свойство
Еще одно важное понятие в сложении — ассоциативное свойство. Оно означает, что группировка чисел при сложении не влияет на итоговую сумму.
Другими словами, если у нас есть три числа, мы можем сначала сложить первые два, а затем прибавить третье число, или мы можем сначала сложить два последних числа, а затем добавить первое число. В обоих случаях получится один и тот же результат.
Например, если у нас есть числа 2, 3 и 4, мы можем сначала сложить 2 и 3, получив 5, а затем прибавить 4, чтобы получить 9. Или мы можем сначала сложить 3 и 4, получив 7, а затем добавить 2, чтобы снова получить 9.
Итак, сложение чисел не так сложно, как может показаться на первый взгляд. Мы можем менять порядок слагаемых и группировать числа, и результат все равно будет одинаковым. Важно помнить о коммутативном и ассоциативном свойствах и использовать их в своих вычислениях.
Вычитание
Основная идея вычитания заключается в том, что мы отнимаем одно число от другого. В этом процессе можно выделить три основных компонента:
- Уменьшаемое: это число, которое мы будем уменьшать или от которого будем отнимать другое число.
- Вычитаемое: это число, которое мы будем вычитать или от которого будем отнимать от уменьшаемого.
- Разность: это результат вычитания, то есть число, которое получается в итоге.
Для выполнения вычитания необходимо выравнять числа по разрядам. Начиная с самого правого разряда, мы вычитаем соответствующие цифры вычитаемого от уменьшаемого. Если уменьшаемое число больше вычитаемого, то просто вычитаем и записываем разность. Если же уменьшаемое число меньше вычитаемого, то мы занимаем единицу из следующего разряда и уменьшаем соответствующий разряд уменьшаемого числа.
Вычитание можно представить в виде таблицы:
| Уменьшаемое | Вычитаемое | Разность |
|---|---|---|
| 4 | 2 | 2 |
| 7 | 5 | 2 |
| 9 | 3 | 6 |
Вычитание — это очень важное математическое действие, которое используется в разных сферах жизни. Например, в торговле вычитание используется для подсчета сдачи и определения стоимости товаров. В финансовой сфере вычитание применяется для бухгалтерии и расчета прибыли. Вычитание также помогает в решении простых уравнений и задач в школьной программе.
Понимание принципов вычитания позволяет нам развивать логическое мышление, улучшать навыки решения задач и рациональную организацию своего времени. Целью вычитания является нахождение точного значения разности между двумя числами и умение применять это знание в повседневной жизни.
Компоненты сложения и вычитания: основные понятия и применение
Компоненты сложения:
- Слагаемые — это числа, которые складываются в процессе операции сложения. Например, в выражении 3 + 5, числа 3 и 5 являются слагаемыми.
- Сумма — это результат операции сложения. В примере 3 + 5, сумма составляет 8.
Компоненты вычитания:
- Уменьшаемое — это число, из которого вычитают другое число в выражении. Например, в выражении 10 — 4, число 10 является уменьшаемым.
- Вычитаемое — это число, которое вычитают из уменьшаемого в выражении. В примере 10 — 4, число 4 является вычитаемым.
- Разность — это результат операции вычитания. В примере 10 — 4, разность составляет 6.
Операции сложения и вычитания широко применяются в повседневной жизни:
- В финансах для подсчета расходов и доходов.
- В торговле для расчета стоимости товаров.
- В строительстве для измерения расстояний или объемов материалов.
- В решении задач и проблем, требующих суммирования или вычитания.
Понимание и умение использовать компоненты сложения и вычитания является важным умением в жизни каждого человека. Это позволяет производить точные расчеты и принимать информированные решения на основе числовых данных.