Координатная плоскость в алгебре для 7 класса: определение и основные понятия

Координатная плоскость — это важный инструмент в алгебре для 7 класса. Она помогает нам представить графически математические объекты, такие как точки, линии и фигуры. Координатная плоскость состоит из двух перпендикулярных осей — оси абсцисс (горизонтальная ось X) и оси ординат (вертикальная ось Y). Точка на плоскости задается двумя числами — координатами (x, y), где x — это расстояние от точки до оси Y, а y — расстояние до оси X.

Основные понятия на координатной плоскости — это точки, оси, положительные и отрицательные координаты, отсчет, расстояние между точками и графики функций. Понимание координатной плоскости позволяет решать уравнения, находить расстояния между точками, строить прямые и находить их уравнения в алгебре. Это важный навык, который поможет в понимании и решении более сложных математических проблем в будущем.

Определение координатной плоскости в алгебре

Оси координат — это две пересекающиеся прямые, горизонтальная и вертикальная, которые образуют систему координат. Они называются осью OX (горизонтальная ось) и осью OY (вертикальная ось).

В центре координатной плоскости находится точка начала координат, обозначаемая буквой O. Она имеет координаты (0, 0), что означает, что она лежит на пересечении осей и расстояние от нее до любой точки на оси равно 0.

Единицы измерения на оси координат — это интервалы, которыми мы измеряем расстояние до точек на координатной плоскости. Они обозначаются числами и могут быть положительными или отрицательными.

Каждая точка на координатной плоскости имеет свои координаты, обозначаемые парой чисел (x, y). Здесь x — значение по горизонтальной оси, а y — значение по вертикальной оси. Такое представление позволяет нам однозначно определить положение точки.

Координатная плоскость в алгебре играет важную роль при решении уравнений, построении графиков и обработке данных. Она помогает нам визуализировать и понимать различные математические концепции и отношения.

Координатная плоскость — что это?

Итак, представьте себе огромную пустую плоскость, где нет ничего, кроме бесконечного количества точек. Замечательно, правда? Так вот, эта плоскость разделена на две оси — горизонтальную и вертикальную. А теперь самое интересное — каждой точке на этой плоскости можно сопоставить уникальную пару чисел, которые называются координатами.

Но что это за числа? Никакой магии, только простые действительные числа. Горизонтальная ось называется осью абсцисс, а вертикальная ось называется осью ординат. И так, каждая точка на плоскости имеет свою уникальную пару чисел, где первое число — это абсцисса, а второе — ордината.

Звучит сложно? Не беспокойтесь! Координатная плоскость — это просто и удивительно полезно. Она помогает нам решать много проблем и задач. Например, мы можем использовать ее для указания местоположения объектов на карте или решения различных уравнений.

Основные понятия координатной плоскости

Каждая точка на координатной плоскости имеет уникальные координаты, которые определяют ее положение. Координаты точки записываются в виде упорядоченной пары чисел (x, y), где x — это значение на оси абсцисс, а y — это значение на оси ординат.

Расстояние между двумя точками на координатной плоскости можно вычислить с помощью формулы дистанции: d = sqrt((x2 — x1)^2 + (y2 — y1)^2), где (x1, y1) и (x2, y2) — координаты двух точек.

На координатной плоскости можно строить графики функций, которые показывают зависимость одной величины от другой. График функции представляет собой множество точек, в которых значения функции соответствуют координатам точек.

Изучение координатной плоскости помогает нам улучшить понимание геометрических и алгебраических концепций, а также применять их на практике для решения различных задач. Так что, друзья, готовы ли вы отправиться в увлекательный мир координатной плоскости и открыть для себя новые математические возможности?

Ось абсцисс и ось ординат

Ось абсцисс — это горизонтальная линия, которая проходит через центр координатной плоскости. Она обозначается буквой «x». Другими словами, это ось, где располагаются числа, соответствующие горизонтальному положению точки.

Ось ординат, с другой стороны, является вертикальной линией, которая также проходит через центр координатной плоскости. Она обозначается буквой «y». Это ось, на которой располагаются числа, соответствующие вертикальному положению точки.

Когда мы используем оси абсцисс и ординат вместе, мы можем определить точное положение любой точки на координатной плоскости. Например, если мы видим точку с координатами (3, 5), это означает, что эта точка находится на 3 единицы вправо от оси абсцисс и на 5 единиц вверх от оси ординат.

Таким образом, оси абсцисс и ординат играют важную роль в алгебре, помогая визуализировать и работать с графиками функций и решать уравнения с неизвестными переменными. Они являются основными инструментами для работы с координатами и понимания положения точек на плоскости.

Определение точки на координатной плоскости

Вы когда-нибудь думали о том, как трудно найти определение для простой точки на плоскости? Ну что ж, я пришел сюда, чтобы разъяснить это!

Точка — это такая замечательная штука. Вы можете представить ее себе как маленькую метку, которую мы ставим на бумаге или на компьютерном экране. Она не имеет размеров, она просто место, где мы хотим сосредоточить внимание. Но как мы можем определить точку в математике?

В математике точка определяется своими координатами на координатной плоскости. Координатная плоскость включает две оси: горизонтальную ось, которая называется осью X, и вертикальную ось, которая называется осью Y. Точка на плоскости определяется своими координатами — X и Y.

Теперь давайте представим, что у нас есть точка с координатами (3, 5). Что это означает? Ищем 3 на оси X и 5 на оси Y, а затем подводим линию, которая соединяет эти две точки. Мы получили нашу точку!

Также возможны отрицательные числа в координатах. Например, (-2, 4). Это означает, что мы находимся 2 единицы влево от начала оси X и 4 единицы вверх от начала оси Y.

Ну что, думаю, теперь вы понимаете, как определить точку на координатной плоскости. Какая точка будет вашей следующей? У вас есть воображение, чтобы отметить ее на бумаге или на экране?

Заключение:

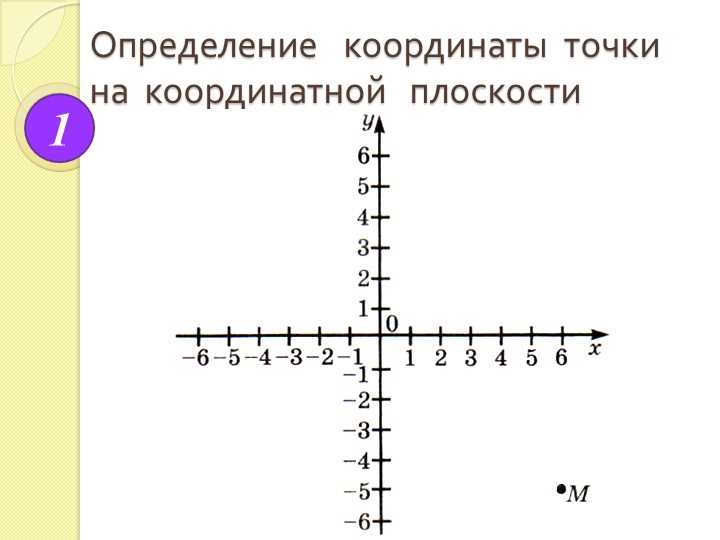
Все эти знания помогут вам лучше понимать графическое представление алгебраических задач и помогут в решении задач разного уровня сложности. Координатная плоскость очень удобна для работы с геометрическими задачами, связанными с алгеброй. Но помимо этого, она имеет и практическое применение в реальной жизни, например, для построения графиков функций и анализа данных.

Таким образом, понимание и использование координатной плоскости в алгебре позволяет развивать логическое мышление, визуальное восприятие и умение анализировать различные задачи с помощью графического представления. Необходимо практиковаться в решении задач с координатной плоскостью, чтобы стать более уверенным и успешным в изучении алгебры и применении ее в различных областях.