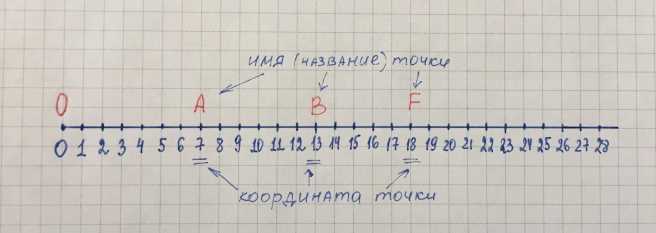
Координатный луч — это прямая линия на числовой оси, которая имеет начальную точку в нуле и располагается в положительной или отрицательной части оси. Например, если координаты лежат в положительной части оси, то они будут больше нуля, а если в отрицательной — меньше нуля.
Примеры координатных лучей: 3, 2, 1, 0, -1, -2, -3. Все числа справа от нуля располагаются на положительном луче, а слева — на отрицательном.
Координатный луч
Дорогой друг, давай поговорим о координатном луче! Может быть, тебе уже удаётся не только определить точку на координатной плоскости, но и провести к ней луч? Если у тебя возникли какие-то вопросы или сомнения, не волнуйся, я помогу тебе разобраться в этом материале!
Координатный луч — это множество точек, начинающихся в точке (0;0) и проходящих через заданную точку. Другими словами, координатный луч — это прямая, которая проходит через начало координат и заданную точку.
Давай рассмотрим это на примере. Представь, что на координатной плоскости мы хотим построить координатный луч, проходящий через точку (3;2). Такой луч будет выглядеть как бесконечная прямая, которая проходит через начало координат (0;0) и точку (3;2). Ты можешь это проверить сам, взглянув на плоскость и прокладывая луч с помощью линейки или карандаша.
Важно помнить, что координатный луч не имеет конца и продолжается бесконечно в положительном и отрицательном направлениях оси координат. Он может пройти через любую заданную точку на плоскости, что делает его очень удобным инструментом для определения направления и расстояния от начала координат до конкретной точки.
Окей, теперь давай попрактикуемся! Представь, что ты хочешь построить координатный луч, проходящий через точку (2;5). Какую прямую нужно провести? Каким будет начало этого луча? А куда он будет направлен? Ты можешь найти ответы на эти вопросы, используя знания о координатных осях и начале координат.
Надеюсь, что тебе стало яснее, что такое координатный луч! Он поможет тебе быстро и уверенно перемещаться по координатной плоскости, находить местоположение точек и решать задачи по координатной геометрии. Так что продолжай исследовать и учиться, и ты сможешь использовать координатный луч с лёгкостью!
Правило определения координатного луча
Дорогой читатель! Сегодня я хочу рассказать тебе о правиле определения координатного луча. Это очень интересное и полезное знание, которое поможет тебе лучше понять геометрию и работу с координатами. Давай разберемся!
Вначале, давай вспомним, что такое координатная плоскость. Это плоскость, на которой мы можем записать точки с помощью пары чисел, так называемых координат. Первое число — это x-координата, а второе — y-координата. Таким образом, каждая точка на плоскости имеет свои уникальные координаты.
Теперь давай узнаем, что такое координатный луч. Координатный луч — это отрезок, который начинается в начале координат и проходит через заданную точку. Он продолжается бесконечно в одном направлении.
Важно помнить, что для определения координатного луча нам необходимо знать только одну точку, через которую он проходит. Это очень удобно, потому что иногда нам может быть сложно определить конечную точку луча, но мы всегда можем проложить луч с помощью известной точки и с помощью правила, которое я скоро расскажу.
Примером использования правила определения координатного луча может быть задача: «Построй координатный луч, проходящий через точку (-3, 4).». Для решения этой задачи мы должны взять нашу известную точку и нарисовать прямую линию, проходящую через начало координат и эту точку. Таким образом, мы построим координатный луч.
Важно учесть, что координатные лучи могут быть направлены в разные стороны в зависимости от заданной точки. Но их начало всегда будет в начале координат.
Теперь, когда мы знаем правило определения координатного луча, давай попрактикуемся в его использовании. Задачка для тебя: «Построй координатный луч, проходящий через точку (2, -5).» Попробуй самостоятельно найти решение, а потом проверь его с помощью ответа ниже:
Чтобы построить координатный луч, мы должны взять точку (2, -5) и провести прямую линию через начало координат и эту точку. Полученная линия будет являться координатным лучом.
Теперь ты знаешь, как определить координатный луч и использовать это правило в задачах. Продолжай практиковаться и развивать свои навыки геометрии!
Примеры координатных лучей
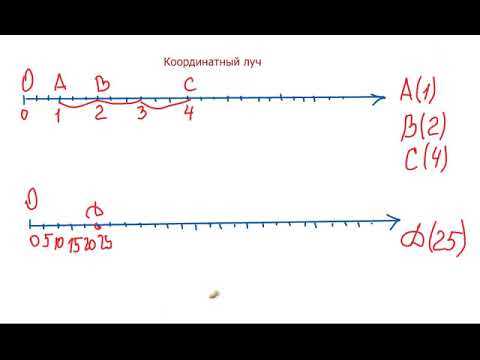
Возьмем, например, координатный луч AB. Он начинается в начале координат, которое обозначается буквой O, и простирается вдоль положительной полуоси абсцисс. Координаты точки B, через которую проходит этот луч, могут быть, например, (4, 0). Это означает, что точка B находится на расстоянии 4 единиц от начала координат по горизонтальной оси (ось абсцисс), а по вертикальной оси (ось ординат) она находится на нулевом расстоянии.
Другой пример — координатный луч CD, который начинается также в начале координат O, но простирается в обратном направлении по отрицательной полуоси абсцисс. Координаты точки D могут быть, например, (-2, 0). Это означает, что точка D находится на расстоянии 2 единиц от начала координат в противоположном направлении (влево) по горизонтальной оси (ось абсцисс), а по вертикальной оси (ось ординат) она находится на нулевом расстоянии.
Также существуют вертикальные и горизонтальные координатные лучи. Например, вертикальный координатный луч EF начинается в начале координат O и простирается вверх по положительной полуоси ординат. Координаты точки F могут быть, например, (0, 5). Это означает, что точка F находится на расстоянии 5 единиц от начала координат по вертикальной оси (ось ординат), а по горизонтальной оси (ось абсцисс) она находится на нулевом расстоянии.
Горизонтальный координатный луч GH начинается также в начале координат O и простирается вправо по положительной полуоси абсцисс. Координаты точки H могут быть, например, (0, 3). Это означает, что точка H находится на расстоянии 3 единиц от начала координат по горизонтальной оси (ось абсцисс), а по вертикальной оси (ось ординат) она находится на нулевом расстоянии.
Использование координатных лучей позволяет наглядно представить и определить положение точки на координатной плоскости. Они являются важным инструментом в работе с алгеброй и геометрией, а также в других областях математики.
Расположение координатного луча на координатной оси
Для понимания расположения координатного луча на координатной оси, представьте себе число ноль — центр координатной оси. Все числа, большие чем ноль, будут располагаться справа от нуля, а числа, меньшие нуля, будут находиться слева от нуля.
Например, если у нас есть координатный луч A и B, где A — положительная часть оси, а B — отрицательная часть оси, то мы можем увидеть, что координатный луч A расположен справа от нуля, а координатный луч B — слева от нуля. А именно, координатный луч A начинается с центра и растягивается вправо до бесконечности, а координатный луч B начинается с центра и растягивается влево до бесконечности.
Расположение координатного луча на координатной оси может быть представлено в виде числовой прямой:
| … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
|---|---|---|---|---|---|---|---|---|
| Координатный луч B | — | — | — | | | … | |||
| Координатный луч A | | | + | + | + | … |
Таким образом, расположение координатного луча на координатной оси дает нам возможность легко определить положение точки на числовой прямой и относительно нуля. Это понимание является важным для изучения математики и решения различных задач, связанных с координатами.
Как находить координатные лучи?
Координатные лучи — это полупрямые, которые простираются из начала координат вдоль осей координат. Их направления и свойства можно легко определить, используя знаки чисел в координатной плоскости.
Для начала давай разберемся с осью X. Если число на оси X положительное, то координатный луч будет направлен вправо. А если число отрицательное, то координатный луч будет направлен влево. На оси Y все немного по-другому. Если число на оси Y положительное, то координатный луч будет направлен вверх. А если число отрицательное, то координатный луч будет направлен вниз.
Рассмотрим примеры, чтобы все сразу стало понятнее. Представь, что у нас есть точка с координатами (3, 2). Определяя знаки чисел, мы понимаем, что координатный луч будет направлен вправо по оси X и вверх по оси Y. Таким образом, координатный луч будет идти вправо и вверх.
А теперь давай рассмотрим другой пример. Представь, что у нас есть точка с координатами (-4, -5). Зная знаки чисел, мы понимаем, что координатный луч будет направлен влево по оси X и вниз по оси Y. Итак, координатный луч будет идти влево и вниз.
Ты уже начинаешь видеть закономерность? Координатные лучи всегда простираются из начала координат в направлении, определенном знаками чисел на оси X и Y.
Но это еще не все! Чтобы полностью понять и применять координатные лучи, необходимо помнить правила и свойства, связанные с ними. Ведь они помогут нам решать задачи и находить точки на координатной плоскости.
Теперь, когда ты знаешь, как находить координатные лучи, ты можешь воспользоваться этим знанием, чтобы легко ориентироваться на координатной плоскости и решать задачи из математики. Попробуй применить это знание в упражнениях и заданиях, и ты будешь уверенно справляться с ними!
Координатный луч: определение и примеры
Для того чтобы определить координатный луч, необходимо задать начальную точку, которая будет являться началом участка прямой. Затем можно определить, что координатный луч будет распространяться в определенном направлении, например, вправо или вверх.
Примеры координатного луча:
- Координатный луч, начинающийся в точке (0, 0) и распространяющийся вправо до бесконечности. В этом случае все точки с положительными значениями координат по оси x будут принадлежать данному координатному лучу.
- Координатный луч, начинающийся в точке (-2, -2) и распространяющийся вверх до бесконечности. В этом случае все точки с положительными значениями координат по оси y будут принадлежать данному координатному лучу.
- Координатный луч, начинающийся в точке (3, 3) и распространяющийся влево до бесконечности. В этом случае все точки с отрицательными значениями координат по оси x будут принадлежать данному координатному лучу.