Координаты 5 класс математика: основные понятия и примеры

Координаты – это понятие, с которым мы встречаемся в математике уже начиная с пятого класса. Они помогают нам точно определить положение объекта на числовой прямой или плоскости. Координаты обычно представляются парой чисел: абсциссой и ординатой.

Абсцисса – это первое число в паре координат. Она определяет положение точки по горизонтальной оси. Ордината – это второе число в паре координат и указывает на положение точки по вертикальной оси.

Например, если мы рассматриваем точку А с координатами (4, 5), то 4 будет абсциссой, а 5 – ординатой. Такие координаты позволяют нам однозначно указать местоположение точки на плоскости и использовать их для решения различных задач.

Поэтому знание и умение работать с координатами – это важный навык для развития математического мышления у учеников пятого класса.

Основные понятия координатной плоскости

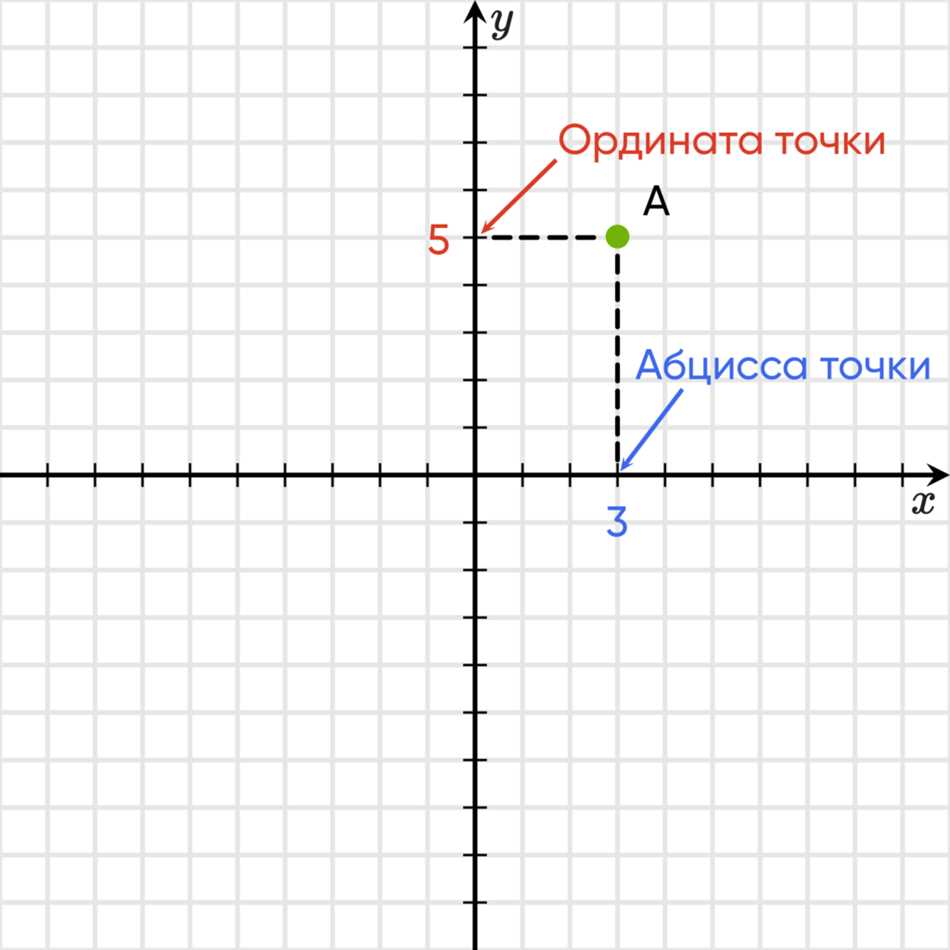
Ось абсцисс горизонтальная линия, а ось ординат вертикальная. Точка пересечения этих линий называется началом координат. Интересное место, не правда ли? А чтобы точно указывать местоположение на координатной плоскости, нам понадобятся координаты.

Координаты точки на плоскости состоят из двух чисел: сначала идет число на оси абсцисс, а затем на оси ординат. Например, точка с координатами (3, 4) находится на 3 единицы вправо от начала и на 4 единицы вверх от начала.

Давайте рассмотрим пример. Если я скажу: «Найди точку с координатами (2, 5)», вы сможете найти ее с легкостью. Двигайтесь на 2 единицы вправо от начала и затем 5 единиц вверх. Вот и она!

Теперь вы знаете основные понятия координатной плоскости. Они не такие страшные, если просто посмотреть на них с другой стороны. Удачи в дальнейшем изучении!

Координатная плоскость

Ось X – это горизонтальная ось, которая расположена слева направо, а ось Y – это вертикальная ось, которая находится снизу вверх. Вся координатная плоскость разбита на много маленьких квадратиков – это единицы измерения на оси X и Y, которые называются делениями.

Теперь вопрос: что такое координаты? Координаты – это числа, которые помогают определить положение точки на координатной плоскости. На самом деле, это просто пара чисел (x, y), где x – это значение на оси X, а y – значение на оси Y.

Координатная плоскость используется во множестве областей, включая геометрию, физику, экономику и программирование. Она помогает нам анализировать и визуализировать информацию с помощью графиков и диаграмм. Используя координатную плоскость, мы можем решать задачи, находить расстояние между точками и многое другое.

Оси координат

Одна ось называется горизонтальной осью или осью абсцисс, а другая – вертикальной осью или осью ординат. На горизонтальной оси мы измеряем расстояние слева направо, а на вертикальной оси – сверху вниз. На пересечении этих осей у нас есть начало координат, точка с координатами (0,0).

Теперь представь, что ты находишься где-то на двухмерной плоскости. Хочешь узнать свои координаты? Очень просто! Просто нужно выяснить, на какой клеточке ты сейчас находишься по горизонтальной и вертикальной оси. Например, если ты находишься на клеточке с координатами (2,4), то по горизонтальной оси ты находишься на второй клетке справа, а по вертикальной оси – на четвертой клетке сверху.

Точка на координатной плоскости

Например, представьте себе точку A. Если мы пишем ее координаты как (2, 3), мы говорим, что она находится 2 единицы вправо от начала координат и 3 единицы вверх. Если координаты точки B — (-5, 0), это означает, что точка находится 5 единиц влево от начала координат и находится на оси абсцисс.

Точки на координатной плоскости могут быть размещены практически везде. Они могут находиться в первом квадранте, где оба значения (x и y) положительные, во втором квадранте, где значение x отрицательное, а значение y положительное, и так далее для третьего и четвертого квадрантов. Они также могут находиться на осях абсцисс или ординат, или даже совпадают в одной точке — начале координат.

Точки на координатной плоскости помогают нам решать различные задачи и строить графики. Они делают наше понимание пространства более точным и помогают визуализировать математические концепции. Их использование может быть очень важно в реальной жизни, например при построении карт, навигации или анализе данных. Поэтому, зная, что такое точка на координатной плоскости и как ее использовать, мы можем быть более уверенными в наших математических навыках и применять их в повседневной жизни.

Координаты точки

Ты уже слышал о понятии «координаты точки»? Если нет, то не беда! Я расскажу тебе все об этом.

Точка на плоскости может быть описана с помощью двух чисел, называемых координатами. Если вспомнить географию, то можешь представить себе карту, на которой каждая точка обозначена своими координатами широты и долготы. В математике у нас тоже есть две оси: горизонтальная (ось абсцисс) и вертикальная (ось ординат).

Например, если мы хотим описать точку «А», то мы должны указать ее координаты на оси абсцисс и ординат. Координаты записываются в виде пары чисел, разделенных запятой: (x, y). Здесь x — значение на оси абсцисс, а y — значение на оси ординат.

А что если точка находится внутри квадрата или на его границе? В таком случае, координаты этой точки будут соответствовать его положению на плоскости.

Надеюсь, что я тебя не запутал еще больше! Если остались еще вопросы, не стесняйся задать. Учиться — это интересно!

Абсцисса и ордината

Абсцисса — это первая координата точки, которая определяет ее положение по горизонтали. Она измеряется вдоль оси X. Представь себе, что это как карта: абсцисса говорит тебе, насколько далеко точка находится от оси Y влево или вправо.

Ордината — это вторая координата точки, которая определяет ее положение по вертикали. Она измеряется вдоль оси Y. Теперь представь, что ты двигаешься вверх и вниз по карте: ордината показывает, насколько высоко или низко находится точка от оси X.

Мы можем использовать абсциссу и ординату вместе, чтобы точно указать местоположение точки на плоскости. Если, например, точка имеет абсциссу 3 и ординату 4, это означает, что она находится на расстоянии 3 вправо и 4 вверх от начала координат.

Использование абсциссы и ординаты помогает нам в решении различных задач и нахождении расстояния между точками на плоскости. Они также позволяют нам строить графики функций и решать геометрические задачи.

Система координат

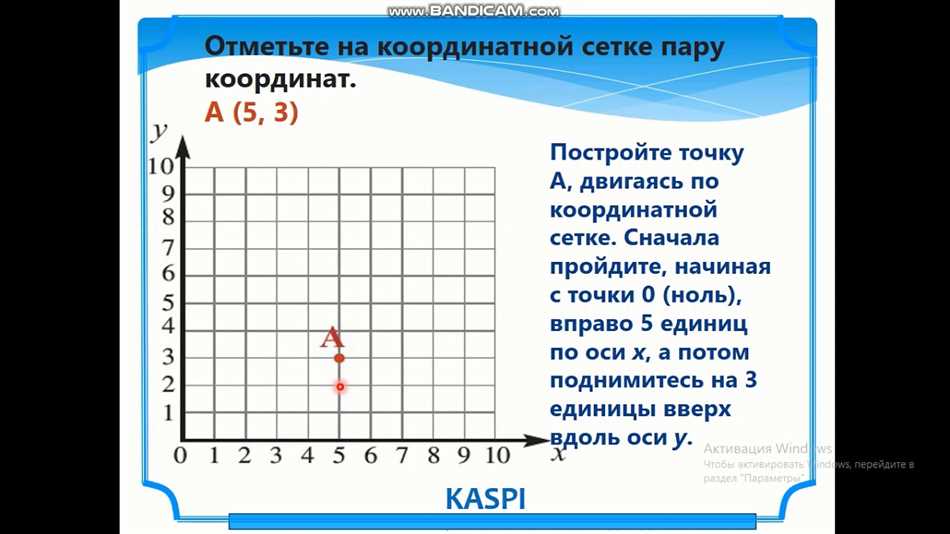
Мы все живем в мире, где все вокруг нас упорядочено и расположено в пространстве. Когда мы говорим о системе координат, мы имеем в виду способ представления этого упорядочения.

Что это значит? Во-первых, представьте себе огромный лист бумаги, на котором нарисованы две перпендикулярные линии. Одна из них называется осью X, а другая — осью Y. В средней точке этих линий находится точка, которая называется началом координат.

Теперь представьте, что вы стоите в этой точке, в центре своего мира. Каждой точке на листе бумаги соответствуют две числа: первое число отражает, как далеко вы находитесь от оси X (влево или вправо), а второе число указывает, насколько вы далеки от оси Y (вверх или вниз).

И все, что нас окружает, может быть представлено в виде точек на этом листе бумаги, используя эти два числа вместе. Например, ваш дом может быть точкой, которая находится на определенном расстоянии от начала координат.

Система координат используется не только математиками, но и другими специалистами в разных областях — от физики до географии. Она помогает нам визуализировать и организовать наше понимание мира вокруг нас.

Заключение

В данной статье мы рассмотрели понятие координат точки и способы задания точки по координатам. Координаты точки определяют ее положение на плоскости и позволяют однозначно идентифицировать точку.

Мы изучили, как задавать точку по координатам на координатной плоскости. Существуют два основных способа: задание точки в виде упорядоченной пары чисел (x,y) и задание разности между заданной точкой и началом координат (Δx,Δy).

Задание точки по координатам является важным навыком для работы с графиками и решения задач на плоскости. Понимание этого концепта позволяет нам анализировать и представлять информацию графически, а также решать задачи с использованием координат.

Знание и понимание работы с координатами также пригодится в будущем при изучении более сложных математических концепций и дисциплин, связанных с геометрией, алгеброй и анализом.