Координаты проекций точек: понятие и примеры

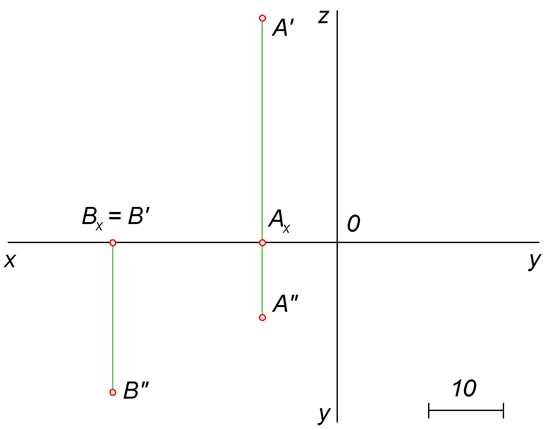
Когда мы говорим о координатах точки, мы обычно имеем в виду ее положение на плоскости. Но что, если нам интересно узнать не только положение точки на плоскости, но и ее положение по отношению к другим плоскостям?

Здесь на помощь приходят координаты проекций точек. Проекция точки — это ее отображение на плоскости, перпендикулярной основной плоскости. Например, если у нас есть точка A на плоскости XY, то мы можем найти ее проекцию на плоскость XZ или YZ.

Координаты проекций точек позволяют нам более точно определить положение точки в пространстве. Они используются в различных областях, включая геометрию, физику и инженерные науки.

Определение и основные понятия

Что такое координаты проекций точек? Это способ задания положения точек в пространстве с помощью чисел. Здорово, не так ли? Ну что, давайте погрузимся в детали.

Координаты проекций точек представляют собой числа, которые определяют положение точек относительно некоторого начала координат. Начало координат — это точка, от которой мы отсчитываем расстояния до остальных точек. В трехмерном пространстве начало координат обычно обозначается буквами X, Y и Z.

Координаты проекций точек могут быть представлены в виде чисел в декартовой системе координат или в других системах координат, таких как сферическая или цилиндрическая. В декартовой системе координат каждая точка имеет три координаты: X, Y и Z, которые представляют собой расстояния по осям X, Y и Z соответственно.

Зачем нам нужны координаты проекций точек? Они позволяют нам точно определить положение объектов в пространстве и использовать их в различных областях, таких как графика, геометрия, физика, архитектура, компьютерная графика и многих других.

Теперь, когда вы знаете, что такое координаты проекций точек и зачем они нам нужны, вы можете использовать их для описания и анализа положения точек и создания удивительных проектов в своей собственной области интересов. Удачи!

Проекции точек на оси координат

Ты когда-нибудь задумывался, что такое проекции? Обычно мы связываем этот термин с кинематографом или архитектурой, но проекции точек играют важную роль и в математике.

В математике проекции точек относятся к их отображению на оси координат. Давай представим, что у нас есть точка в двумерном пространстве со значениями (x, y). Ее проекции на оси координат представляют собой отдельные значения x и y.

Проекция точки на ось x представляет собой значение координаты x, а проекция точки на ось y — значение координаты y. Эти значения могут быть положительными или отрицательными, в зависимости от положения точки относительно начала координат.

Проекции точек на оси координат позволяют нам легко определить положение точки в пространстве. Например, если проекция точки на ось x равна 5, а проекция точки на ось y равна -3, то мы можем сказать, что это точка находится на пятом горизонтальном ряду и третьем вертикальном ряду от начала координат.

Понимание проекций точек на оси координат полезно не только в математике, но и в реальной жизни. Например, при работе с картами или GPS-навигацией мы используем проекции точек для определения местоположения или расстояния до цели.

Координаты проекций точек в двухмерном пространстве

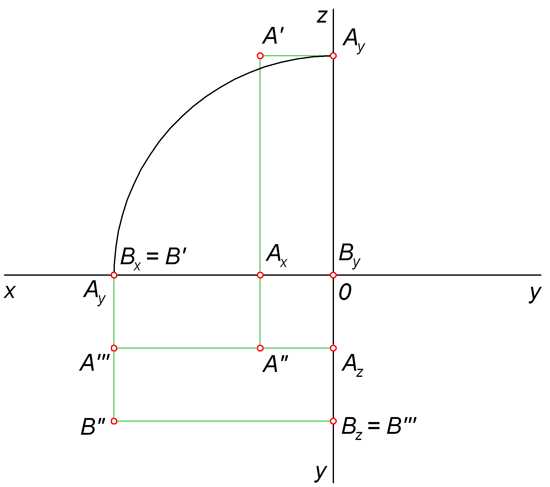
Когда мы говорим о координатах проекций точек в двухмерном пространстве, мы обычно имеем в виду их положение на плоскости. Ведь в двухмерном пространстве у нас есть только два измерения: длина и ширина.

Таким образом, координаты проекций точек представляют собой числа, показывающие расстояние от точки до осей, на которых определено наше пространство. Обычно, мы используем систему координат, состоящую из двух взаимно перпендикулярных осей, называемых осью X (горизонтальная ось) и осью Y (вертикальная ось).

На этой системе координат каждая точка имеет свои координаты. Координата X указывает, как далеко точка находится от вертикальной оси Y, а координата Y показывает, как далеко точка находится от горизонтальной оси X. Например, если у нас есть точка с координатами (3, 2), это означает, что она находится 3 единицы по горизонтали от вертикальной оси Y и 2 единицы по вертикали от горизонтальной оси X.

Знание координат проекций точек позволяет нам определить их положение на плоскости, измерять расстояния между точками и выполнять другие геометрические операции. Оно также является основой для работы с двумерными графическими объектами, такими как фигуры и изображения, в компьютерной графике и дизайне.

Проекции точек на плоскость и пространство

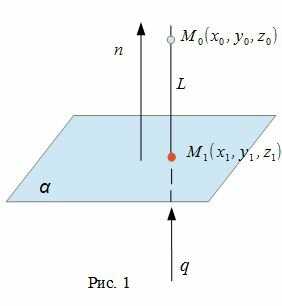
Вот представь: у тебя есть точка в пространстве, а у тебя есть плоскость, на которую ты хочешь проецировать эту точку. Ты берешь перпендикуляр к плоскости и от этой точки опускаешь на перпендикуляр луч, которого длина равна расстоянию до плоскости. И вот, точка, где этот луч пересечется с плоскостью – это и есть проекция точки на эту плоскость.

Важно помнить, что проекция точки на плоскость не может быть точкообразной, она всегда имеет размеры. Если мы рассматриваем проекцию точки на плоскость, то это будет точка на этой плоскости. А вот проекция точки на пространство образуется в виде линии, она как бы показывает путь, по которому точка движется от перпендикуляра до плоскости.

Применение и практическое значение координат проекций точек

Применение координат проекций точек находит свое применение в различных областях. Например, в архитектуре они используются для создания планов зданий или других объектов. Точки на плане обозначаются координатами проекций, что позволяет инженерам и архитекторам точно определить расположение элементов конструкции.

Координаты проекций также применяются в геодезии для измерения и описания земли и ее формы. Геодезисты используют координаты проекций точек для создания карт, определения высот, а также для точного определения границ и площадей земельных участков.

Координаты проекций точек играют ключевую роль в компьютерной графике и компьютерных системах. Они используются при создании трехмерных моделей объектов, отображении изображений на экране и определении положения курсора мыши.

• Применение и практическое значение координат проекций точек включает:
• Определение положения элементов конструкций в архитектуре и инженерии.
• Измерение и описание земли в геодезии.
• Создание трехмерных моделей объектов в компьютерной графике.
• Определение положения курсора мыши в компьютерных системах.