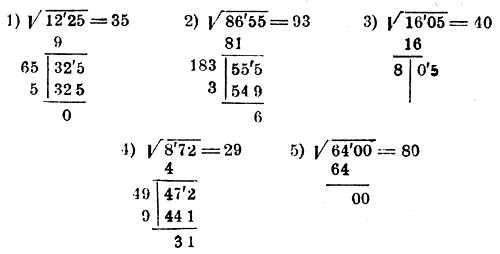
Корень квадрат: определение, примеры, свойства

Корень квадрата – это математическое понятие, которое исполняет главную роль в алгебре и геометрии. Уравнение вида «x в квадрате равно а» можно представить в виде «x равно корень квадратный из а». В своей сути, корень квадратный – это число, которое умноженное на себя дает другое число.

Взять корень квадратный из числа – значит найти число, которое возведенное в квадрат равно данному числу. Например, корень квадратный из 16 равен 4, так как 4 возводим в квадрат равно 16.

Корень квадратный имеет свои особенности и применяется во многих областях, начиная от физики и заканчивая архитектурой.

Определение корня квадратного

Корень квадратный связан с понятием квадрата числа. Знаешь ли ты, что квадрат числа получается, если это число умножить на себя? Например, квадрат числа 4 равен 4 умноженное на 4, то есть 4 * 4 = 16.

Теперь представь, что мы знаем квадрат числа 16 и хотим найти само число, из которого это квадрат получился. Здесь на помощь приходит корень квадратный! Корень квадратный числа 16 равен 4, так как 4 * 4 = 16.

Кроме того, корень квадратный может быть не только у положительных чисел, но и у отрицательных. В таком случае, мы используем символ «i», чтобы обозначить мнимую единицу. Например, корнем квадратным числа -4 будет 2i, так как 2i * 2i = -4.

И вот, мы разобрались с тем, что такое корень квадратный. Надеюсь, тебе было интересно и понятно! Если у тебя возникли вопросы, задавай их без стеснения. Рад буду помочь! Хорошего дня!

Основные понятия

Допустим, у нас есть число 25. Как нам найти корень квадратный из него? Просто найдем число, которое, возводимое в квадрат, даст нам 25. И вот мы получаем число 5. Значит корень квадратный из 25 равен 5. Просто магия, не так ли?

Но почему это важно? Корень квадратный помогает нам решать различные задачи как в математике, так и в реальной жизни. Например, он может быть использован для расчета сторон прямоугольника или для определения расстояния между двумя точками на плоскости.

Так что не бойтесь корня квадратного — он не такой уж и сложный. Вместо этого давайте посмотрим на него как на удивительный инструмент, который может помочь нам лучше понимать мир вокруг нас.

Примеры вычисления квадратного корня

Процесс вычисления квадратного корня может показаться сложным, но на самом деле это довольно просто, особенно если использовать калькулятор. Вот несколько примеров вычисления квадратного корня:

• Пример 1: Пусть нам нужно найти квадратный корень из числа 25. Мы можем заметить, что 5 * 5 = 25, поэтому квадратный корень из 25 равен 5.
• Пример 2: Пусть нам нужно найти квадратный корень из числа 9. Здесь мы также можем заметить, что 3 * 3 = 9, поэтому квадратный корень из 9 равен 3.
• Пример 3: Теперь рассмотрим число 20. В данном случае нет целого числа, которое умноженное само на себя давало бы 20, поэтому мы должны найти приближенное значение. Приближенный квадратный корень из 20 можно найти, например, методом деления отрезка пополам. Используя этот метод, мы можем сделать несколько итераций и приблизиться к значению 4.47.

Вот несколько примеров вычисления квадратного корня. Практикуйтесь в их решении, и вскоре вы сможете легко и быстро находить квадратные корни различных чисел!

Свойства корня квадратного

Одно из главных свойств корня квадратного — это его неотрицательность. Все корни квадратные неотрицательны, то есть они всегда больше или равны нулю. Представь себе, что мы пытаемся извлечь корень квадратный из отрицательного числа, например, -9. С такой операцией мы столкнемся с проблемой, так как нет никакого числа, которое при возведении в квадрат дала бы нам -9. Поэтому корень квадратный из отрицательного числа не определен.

Корень квадратный также обладает свойством иррациональности, то есть он может быть представлен в виде бесконечной десятичной дроби, которая не может быть точно представлена в виде обыкновенной дроби. Например, корень квадратный из числа 2 равен приблизительно 1,41421356 и т.д., что не может быть представлено конечной десятичной дробью или обыкновенной дробью.

Кроме того, корень квадратный обратный операции возведения в квадрат. Если мы возведем число в квадрат и затем извлечем из него корень квадратный, мы получим исходное число. Например, корень квадратный из числа 25 равен 5, поскольку 5 в квадрате будет 25.

Так что, не бойся использовать корень квадратный в математике! Он имеет много интересных свойств и применений в нашей повседневной жизни.

Использование корня квадратного в математике

Корень квадратный – это операция, которая позволяет нам найти число, если его квадрат равен известному числу. Например, если мы знаем, что квадрат числа 9 равен 81, мы можем найти корень квадратный из 81, который будет равен 9. То есть, корень квадратный извлекает из числа его «исходник», его основу. Он помогает нам найти значение, которое нужно в задаче или уравнении.

Корень квадратный также широко используется в геометрии, в особенности при вычислении длин сторон прямоугольного треугольника. Если мы знаем длину одной стороны и хотим найти длину другой стороны, мы можем использовать формулу для нахождения корня квадратного.

Интересно, что корень квадратный часто встречается в повседневной жизни, хоть мы и не задумываемся об этом. Например, при покупке квадратного ковра, нам нужно знать его длину или сторону. Для этого мы можем использовать корень квадратный, чтобы найти нужное значение.

В общем, корень квадратный – это полезный инструмент в математике, который помогает нам находить неизвестные значения, работать с геометрическими фигурами и применять математические знания в повседневной жизни. Не забывайте использовать его и экспериментировать с различными задачами – это поможет вам лучше понять и полюбить эту потрясающую науку!

Корень квадратный в реальной жизни

Давайте поговорим о корне квадратном и о том, как мы можем его встретить в нашей повседневной жизни.

Во-первых, корень квадратный может быть полезен при решении задач физики, особенно связанных с движением тела. Например, если мы хотим вычислить скорость, расстояние или время на основе известных физических данных, нам может потребоваться извлечь корень квадратный для получения точного результата.

Во-вторых, корень квадратный может пригодиться, когда мы работаем с геометрическими фигурами. Например, если мы знаем площадь квадрата, нам может понадобиться найти сторону этого квадрата, и для этого нам придется использовать корень квадратный. Также при вычислении длины диагонали прямоугольника или треугольника мы обязательно встретимся с корнем квадратным.

Корень квадратный имеет и другие практические применения. Например, в финансовой сфере он может использоваться для расчета процентной ставки или прибыли по инвестициям. А в строительстве — для определения длины строительных конструкций или расчета площади помещения.

Таким образом, корень квадратный является полезным математическим инструментом в нашей повседневной жизни. Он помогает нам уточнить результаты вычислений, решить задачи физики и геометрии, а также применяться в различных областях от финансов до строительства. Поэтому, знание этой математической операции очень важно и может быть полезно в самых неожиданных ситуациях.

Практические задачи с корнем квадратным

Однако, знание теории не всегда позволяет с легкостью решить практические задачи, в которых используется корень квадратный. Ниже представлены некоторые примеры таких задач на применение корня квадратного в повседневной жизни:

1. Расчет расстояния: Допустим, вы хотите определить расстояние между двумя точками на плоскости. Если известны координаты этих точек, то можно воспользоваться формулой расстояния между двумя точками в декартовой системе координат. В этой формуле используется корень квадратный для нахождения длины отрезка.

2. Расчет площади: Представим, что вам необходимо рассчитать площадь фигуры. В некоторых случаях можно воспользоваться формулой, которая требует вычисления корня квадратного, например, для нахождения длины стороны квадрата или радиуса окружности.

3. Определение времени: Пусть вам известна скорость и время движения объекта. С помощью корня квадратного можно вычислить расстояние, пройденное этим объектом.

Это лишь несколько примеров применения корня квадратного в практических задачах. Корень квадратный является важным инструментом не только в математике, но и в других областях науки и промышленности. Разностороннее практическое использование этой математической операции позволяет решать различные задачи и находить точные решения в реальном мире.