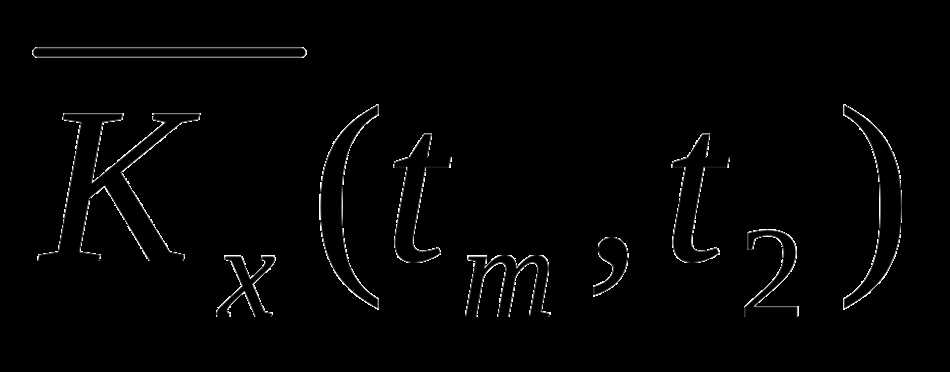
Корреляционная функция случайного процесса — это способ описания связи между значениями случайного процесса в разные моменты времени. Она позволяет понять, насколько зависимы между собой различные точки процесса. Корреляционная функция выражает меру схожести между значениями случайного процесса в разные моменты времени: чем ближе к единице значение корреляционной функции, тем сильнее зависимы между собой значения процесса в данных моментах времени.
Корреляционная функция может быть использована для анализа и прогнозирования процессов в различных областях, таких как физика, экономика и биология. Например, при исследовании финансовых данных корреляционная функция может помочь определить, есть ли связь между доходностью различных акций, а также предсказать будущие движения цен.
Изучение корреляционной функции позволяет понять природу случайных процессов и их взаимосвязь во времени. Это важный инструмент для анализа данных и принятия решений на основе статистических моделей.
- Общая информация
- Определение корреляционной функции
- Применение корреляционной функции
- Формула корреляционной функции
- Примеры использования корреляционной функции
- Преимущества корреляционной функции
- Вопрос-ответ:
- Зачем нужна корреляционная функция?
- Какую информацию можно получить с помощью корреляционной функции?
- Как использовать корреляционную функцию в практических задачах?
Общая информация
Еще один пример – финансовые данные. Мы можем использовать корреляционную функцию для определения взаимосвязи между доходностью двух акций. Если мы обнаружим высокую корреляцию между доходностью акций, то это может указывать на наличие некоторых общих факторов, влияющих на оба актива.
Корреляционная функция помогает нам лучше понять и анализировать случайные процессы и извлекать полезную информацию из них. Она широко используется в различных областях, включая науку о данных, экономику, физику и многое другое.
Определение корреляционной функции

Корреляционная функция принимает значения от -1 до 1. Значение -1 означает полную обратную зависимость: когда одна величина возрастает, другая убывает и наоборот. Значение 1 указывает на полную прямую зависимость: когда одна величина возрастает, другая также возрастает и наоборот. Значение 0 означает отсутствие линейной зависимости между величинами.
Корреляционная функция имеет широкое применение в различных областях, таких как финансы, экономика, социология и естественные науки. Она помогает нам понять, какие факторы влияют на изменение случайного процесса и как их можно предсказать или контролировать.
Применение корреляционной функции
В статистике корреляционная функция используется для анализа зависимостей между различными переменными. Она позволяет оценить степень связи между двумя переменными и определить, как изменение одной переменной влияет на другую. Например, корреляционная функция может быть использована для изучения зависимости между количеством продаж и рекламными затратами.
В экономике корреляционная функция применяется для анализа зависимостей между различными экономическими переменными. Она позволяет выявить, как изменения в одной переменной могут влиять на другие переменные и определить, какие факторы могут влиять на экономический результат.
В физике корреляционная функция используется для изучения связи между различными физическими величинами. Она позволяет определить, как изменение одной величины может быть связано с изменением другой и какие факторы могут влиять на физический процесс.
В общем, корреляционная функция является мощным инструментом для изучения зависимостей и прогнозирования будущих результатов. Она позволяет определить, как одна переменная влияет на другую и помогает выявить факторы, которые могут быть релевантными для анализа. Вы можете применить эту функцию в различных областях и находить интересные зависимости и взаимосвязи между различными переменными. Вот и все!
Формула корреляционной функции
Когда мы говорим о корреляционной функции случайного процесса, мы обращаемся к мере, которая показывает, насколько два случайных события связаны друг с другом. Или, проще говоря, насколько их изменения сходны или противоположны.
Формула для расчета корреляционной функции выглядит следующим образом:
R(t1, t2) = E{X(t1) * X(t2)}
Где R(t1, t2) — корреляционная функция, E — математическое ожидание случайной величины, а X(t1) и X(t2) — значения случайного процесса в моменты времени t1 и t2 соответственно.
В более простых терминах, мы умножаем значения случайного процесса в двух разных моментах времени и находим среднее значение этого произведения. Это позволяет нам определить, насколько сильная связь между ними.
Корреляционная функция является важной концепцией в статистике и помогает нам понять, какие случайные события взаимосвязаны и как они могут влиять на друг друга. Она используется во многих областях, таких как финансы, экономика, метеорология и телекоммуникации, чтобы предсказывать и анализировать данные.
Примеры использования корреляционной функции

Один из примеров использования корреляционной функции – анализ финансовых рынков. Путем изучения корреляций между доходностью различных активов в портфеле, инвесторы могут оценить риск и выгоду от выбранного сочетания активов. Корреляция обычно измеряется с помощью корреляционной функции, которая может указать на схожую динамику доходности активов или на их независимость.
Еще одним примером использования корреляционной функции является анализ связи между двумя переменными в научных исследованиях. Например, в медицинских исследованиях корреляционная функция может помочь выявить взаимосвязь между уровнем физической активности и заболеваемостью определенными заболеваниями. Такая информация может быть полезной для разработки интегрированных программ здоровья и предотвращения заболеваний.
В области техники и инженерии корреляционная функция может использоваться для анализа пути сигналов или шумов в системах связи или радиотехнике. Понимание корреляций между различными сигналами может помочь в оптимизации процессов передачи данных или в улучшении качества связи.
Преимущества корреляционной функции
- Определение зависимости: Корреляционная функция позволяет определить взаимосвязь между случайными величинами и выявить зависимости между ними. Это особенно полезно при исследовании сложных систем, где множество факторов могут влиять на результаты.
- Прогнозирование будущих значений: Корреляционная функция может использоваться для прогнозирования будущих значений случайного процесса. На основе ранее наблюдаемых значений и корреляционной функции можно построить модель и предсказать будущие значения.
- Определение параметров случайного процесса: Корреляционная функция позволяет оценить различные параметры случайного процесса, такие как дисперсия, коэффициент вариации и другие. Это позволяет более точно описать и понять свойства случайного процесса.
В целом, корреляционная функция является мощным инструментом для анализа случайных процессов и имеет широкий спектр применений в различных областях, включая экономику, физику, финансы, медицину и другие. Она помогает в выявлении и понимании зависимостей, прогнозировании будущих значений и определении параметров случайного процесса.
Вопрос-ответ:
Зачем нужна корреляционная функция?
Корреляционная функция позволяет определить наличие и степень связи между двумя или более переменными. Она является важным инструментом в анализе данных и находит широкое применение в различных областях, таких как экономика, физика, психология и другие. С помощью корреляционной функции можно выявить зависимости между переменными, предсказывать будущие значения, а также проверять статистическую значимость этих зависимостей.
Какую информацию можно получить с помощью корреляционной функции?
Корреляционная функция позволяет узнать не только наличие связи между переменными, но и ее направление и силу. Например, положительная корреляция означает, что значения двух переменных изменяются в одном направлении, то есть при увеличении одной переменной, увеличивается и другая. Отрицательная корреляция, напротив, означает, что значения переменных меняются в противоположных направлениях: увеличение одной переменной сопровождается уменьшением другой. Кроме того, корреляционная функция может дать представление о форме связи между переменными: линейная, нелинейная, монотонная и др.
Как использовать корреляционную функцию в практических задачах?
Корреляционная функция может быть полезна во многих практических задачах. Например, она может помочь в предсказании будущих значений переменных на основе данных их предыдущих значений. Также с помощью корреляционной функции можно определить влияние одной переменной на другую и использовать эту информацию для принятия решений или планирования. Корреляционная функция также может быть использована для идентификации аномалий или выбросов в данных. Наконец, она может быть полезна в построении моделей и прогнозировании поведения систем.