Косинусное расстояние – это метрика, которая позволяет измерить сходство между двумя векторами в многомерном пространстве. Она широко используется в различных областях, таких как машинное обучение, естественный языкобработка и информационный поиск.
Косинусное расстояние рассчитывается по формуле, основанной на косинусе угла между двумя векторами. Оно измеряет сходство путем изучения, насколько эти векторы направлены в одном и том же направлении. Если угол между векторами равен 0°, то косинусное расстояние будет равно 1, что означает полное сходство.
Чем ближе значение косинусного расстояния к 1, тем больше сходство между векторами. Если же значение ближе к 0, то векторы считаются менее схожими.
Косинусное расстояние является полезным инструментом для сравнения и анализа данных, позволяющим определить степень сходства между ними.
Косинусное расстояние: Определение
Ты когда-нибудь задумывался, что такое косинусное расстояние? Если да, то давай разбираться вместе.
Косинусное расстояние — это мера сходства между двумя векторами в многомерном пространстве. Оно измеряет угол, который образуют эти векторы, и позволяет определить, насколько они похожи или различаются. Чем меньше угол между векторами, тем ближе они друг к другу, а значит, тем больше их сходство.
Если представить, что векторы — это точки на графике, то косинусное расстояние можно интерпретировать как меру близости этих точек. Например, если две точки находятся рядом, то их косинусное расстояние будет мало, а если они далеко друг от друга, то оно будет большим.
Косинусное расстояние широко используется в различных областях, таких как машинное обучение, компьютерное зрение и информационный поиск. Оно помогает сравнивать и классифицировать данные, находить похожие объекты и определять их сходство.
Применение косинусного расстояния
Представьте, что у вас есть большой набор документов, и вам необходимо найти наиболее похожие документы на заданный запрос. Вот где косинусное расстояние подходит как нельзя кстати! Вы можете представить каждый документ в виде вектора, где каждый элемент — это вес термина в документе. Затем сравните косинусные расстояния между вектором запроса и векторами документов, чтобы определить наиболее релевантные.
Еще одно практическое применение косинусного расстояния связано с анализом текста. Допустим, вы хотите сравнить два текста и понять, насколько они похожи друг на друга. Снова вы можете представить каждый текст в виде вектора слов и вычислить косинусное расстояние между ними. Чем меньше расстояние, тем более похожи тексты.
Кроме того, косинусное расстояние может быть полезно для кластеризации данных, классификации документов, коллаборативной фильтрации и даже для анализа изображений. Его гибкость и простота в использовании делают его мощным инструментом в машинном обучении и анализе данных.
Так что, если у вас есть данные, которые нужно сравнить или категоризировать, не забудьте о возможности использовать косинусное расстояние — это может быть ключом к нахождению интересных закономерностей и знаний, спрятанных в ваших данных.
Вычисление
Когда мы говорим о вычислении косинусного расстояния, мы обычно имеем в виду вычисление угла между двумя векторами. Но что это за угол и как его вычислить?
Во-первых, нам нужно знать, что косинусное расстояние является мерой сходства или различия между двумя векторами. Оно показывает, насколько похожи или отличаются два вектора в пространстве. Чем ближе косинусное расстояние к 1, тем более похожи векторы, а если оно близко к 0 или имеет отрицательное значение, значит, векторы сильно отличаются.
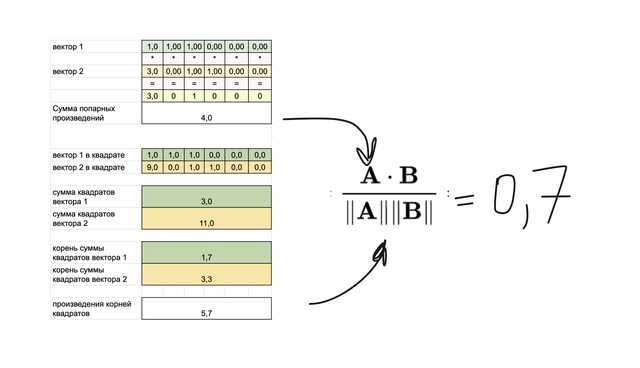
Чтобы вычислить косинусное расстояние, мы используем формулу, которая основана на вычислении скалярного произведения и длины векторов. Как правило, мы делим скалярное произведение на произведение длин векторов, чтобы получить косинус угла между ними.
Математически, формула выглядит так:
cosine_similarity(A, B) = (A · B) / (||A|| * ||B||)
Где A · B — скалярное произведение векторов A и B, а ||A|| и ||B|| — длины этих векторов. Подставляя значения в эту формулу, мы получаем косинусное расстояние.
Особенности использования косинусного расстояния
Одной из основных особенностей косинусного расстояния является его нечувствительность к длине векторов. Это означает, что сходство двух объектов не зависит от их абсолютной величины, а только от соотношения их компонент. Это очень полезное свойство, особенно при работе с текстовыми данными, где длина документов может сильно варьироваться.
Кроме того, косинусное расстояние также обладает транзитивностью и метрическим свойством, что делает его удобным для выполнения операций схожести и поиска ближайших соседей. Однако следует помнить, что косинусное расстояние не учитывает некоторые структурные аспекты данных, такие как порядок и последовательность, и может оказаться неэффективным в некоторых случаях.
В конечном счете, выбор использования косинусного расстояния зависит от конкретной задачи и типа данных, с которыми вы работаете. Он является мощным инструментом для измерения сходства объектов и может быть применен во многих областях. Тем не менее, необходимо учитывать его ограничения и применять его с умом, чтобы получить наиболее точные и интерпретируемые результаты.
Вопрос-ответ:
Какие особенности использования нужно учесть?
При использовании данной техники необходимо учитывать следующие особенности: совместимость с операционными системами, требования к аппаратным ресурсам, наличие необходимого программного обеспечения, возможность подключения к сети интернет и др.
Какие преимущества имеет использование данной техники?
Использование данной техники обладает рядом преимуществ: повышение эффективности работы, увеличение скорости выполнения задач, улучшение качества обслуживания клиентов, сокращение времени на ожидание и многое другое.
Какие недостатки могут быть при использовании данной техники?
Некоторые недостатки использования данной техники могут включать в себя: высокую стоимость, сложность настройки, потребность в обучении персонала, возможность возникновения ошибок в работе и другие.