Крайние и средние пропорции: понятие и области применения

Пропорции — это математическое соотношение между различными элементами или составляющими целого. В архитектуре, искусстве и дизайне, пропорции играют важную роль в создании гармоничного и эстетически привлекательного вида. Одним из способов достижения этой гармонии является использование крайних и средних пропорций. Крайние пропорции, известные также как «золотое сечение», стремятся к созданию идеального баланса, в то время как средние пропорции обеспечивают более смешанный и живой характер. В этой статье мы рассмотрим определение и примеры использования крайних и средних пропорций в различных областях.

Крайние и средние пропорции: определение и примеры использования

Крайние пропорции, также известные как золотое сечение или золотая пропорция, относятся к соотношению двух величин, где отношение между первой и второй величиной равно отношению между суммой этих двух величин и первой величиной. Это соотношение приближается к числу φ (фи), которое равно приблизительно 1,618. Крайние пропорции используются в архитектуре для создания гармоничных и пропорциональных зданий, в искусстве для композиции и баланса, а также в дизайне интерфейсов и логотипов.

Средние пропорции, также известные как арфиметические прогрессии, относятся к соотношению трех или более чисел, где каждое следующее число является средним арифметическим двух предыдущих чисел. Например, если у нас есть числа 2, 4 и 6, то среднее число между 2 и 4 будет 3, а между 4 и 6 — 5. Средние пропорции широко применяются в финансовых расчетах, статистике и науке для вычисления средних значений, прогнозирования трендов и определения паттернов.

Примеры использования крайних и средних пропорций можно найти везде вокруг нас. Посмотрите на высокое здание, как Burj Khalifa в Дубае, и вы заметите, что его высота и ширина соотносятся по золотому сечению. Взгляните на знаменитые картины Рембрандта или Леонардо да Винчи, и вы обнаружите, что композиция произведений искусства включает крайние пропорции для достижения эстетической гармонии. Финансовые аналитики и экономисты используют средние пропорции для прогнозирования роста и падения рынка, а научные исследователи применяют их для анализа данных и вычисления средних значений в экспериментах.

Крайние и средние пропорции — это мощные инструменты, которые помогают нам стремиться к гармонии и балансу в нашей жизни и окружающей среде. Используйте их в своей работе, и вы увидите, как они могут сделать вашу жизнь более пропорциональной и эстетичной.

Как определить крайние пропорции

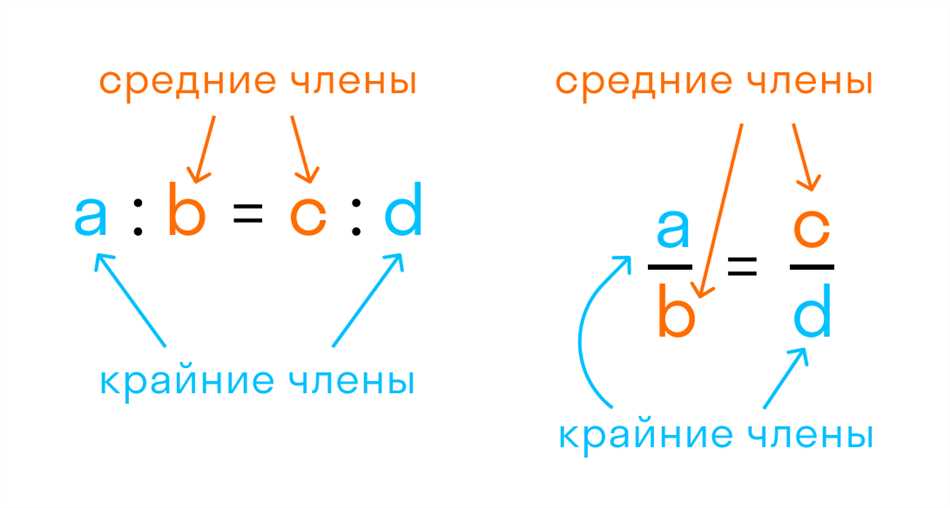
Когда мы говорим о пропорциях, мы обычно думаем о соотношении между различными частями целого. Но что такое крайние пропорции и как их определить?

Крайние пропорции — это специальный тип пропорции, в котором отношение двух частей одинаково с отношением двух других частей. Иными словами, если у нас есть четыре числа — a, b, c и d — то мы можем сказать, что они находятся в крайних пропорциях, если a/b = c/d.

Но как же мы можем определить, находятся ли эти числа именно в крайних пропорциях? Просто сравнить отношения a/b и c/d не будет достаточно. Вместо этого мы должны убедиться, что их отношение равно отношению верхних и нижних частей других двух частей. Иначе говоря, мы должны проверить, что a/b = c/d = (a+c)/(b+d).

Например, давайте рассмотрим следующую ситуацию: у нас есть два таких же стакана с водой. В первом стакане 2 литра воды, а во втором – 4 литра. Мы можем сказать, что количество воды в первом стакане в два раза меньше, чем во втором стакане, и это будет соответствовать отношению 2/4 = 1/2.

Теперь давайте добавим 3 литра воды в первый стакан и 6 литров во второй. Теперь отношение между ними также будет равно 3/6 = 1/2. Мы видим, что даже после добавления дополнительной воды отношение между количеством воды в стаканах не изменилось.

Таким образом, в этом примере мы можем сказать, что количество воды в стаканах находится в крайних пропорциях. Однако, в других ситуациях может быть не так просто определить, находятся ли числа в крайних пропорциях или нет. Поэтому часто требуется дополнительный анализ и расчеты.

В конечном итоге, умение определить крайние пропорции может быть полезным для решения различных математических задач и применений в повседневной жизни. Благодаря этому навыку мы можем лучше понимать соотношение между различными частями и использовать его для проведения анализа и прогнозирования.

Примеры использования крайних пропорций

1. Дизайн веб-сайтов

Крайние пропорции играют важную роль в создании привлекательных и гармоничных визуальных композиций при разработке веб-сайтов. Они могут быть использованы для распределения элементов на странице, создания сетки и определения размеров объектов. Например, крайние пропорции могут помочь определить, как расположить заголовки, текст и изображения на странице, чтобы создать эстетически приятный и легкий для восприятия макет.

2. Фотография

В фотографии крайние пропорции могут быть использованы для создания баланса и гармонии в композиции. Например, закон третей иногда используется для размещения центрального объекта или главного фокуса в одной из внешних третей фотографии. Это помогает создать привлекательный и сбалансированный снимок.

3. Искусство и архитектура

Крайние пропорции играют важную роль в искусстве и архитектуре. Великие художники и архитекторы часто используют крайние пропорции, такие как золотое сечение или пропорции Фибоначчи, чтобы создавать прекрасные и эстетически приятные произведения и конструкции. Эти пропорции помогают достичь гармонии и баланса в композиции и делают искусство привлекательным для глаза наблюдателя.

4. Дизайн логотипов

Крайние пропорции также широко используются в дизайне логотипов. Они помогают создать сбалансированный и запоминающийся логотип, который привлекает внимание и передает конкретное сообщение. Крайние пропорции могут быть использованы для определения размеров, формы и расположения элементов логотипа, чтобы создать гармоничное и эффективное визуальное изображение бренда.

5. Графический дизайн

В графическом дизайне крайние пропорции могут быть использованы для создания сбалансированных композиций, определения размеров и расположения элементов, а также для создания гармоничных и эстетически приятных изображений. Например, крайние пропорции могут помочь определить, как расположить текст и изображения на плакате или баннере, чтобы создать эффективное и запоминающееся визуальное сообщение.

Это только некоторые примеры использования крайних пропорций. Они демонстрируют, как важен этот инструмент в различных областях нашей жизни. Используйте их с умом и креативно, чтобы создать эстетически привлекательные и гармоничные композиции и произведения искусства.

Как определить средние пропорции

Вы наверняка слышали о понятии «средние пропорции» и задумывались, как их определить. Давайте разберемся в этом вопросе!

Средние пропорции — это способ определить среднее значение в наборе чисел или данных. Они используются в различных областях, таких как статистика, бизнес и наука.

Существует несколько способов определения средних пропорций, но наиболее распространенный способ — это вычисление среднего арифметического. Это простой способ, который подходит для большинства задач и представляет общее среднее значение в наборе данных.

Для определения среднего арифметического, нужно сложить все числа в наборе и разделить их на количество чисел. Например, если у нас есть набор чисел: 5, 8, 12, 6 и 10, мы должны сложить их вместе: 5 + 8 + 12 + 6 + 10 = 41. Затем разделим сумму на количество чисел в наборе: 41 / 5 = 8.2. Таким образом, среднее арифметическое для данного набора чисел равно 8.2.

Еще одним способом определения средних пропорций является медиана. Медиана — это среднее значение, которое находится посередине набора данных, когда он упорядочен в порядке возрастания или убывания. Если у нас есть набор чисел: 5, 8, 12, 6 и 10, мы должны упорядочить их: 5, 6, 8, 10, 12. Затем мы находим число, которое находится посередине: 8. Таким образом, медиана для данного набора чисел равна 8.

Другим способом определения средних пропорций является мода. Мода — это число или числа, которые встречаются наиболее часто в наборе данных. Если у нас есть набор чисел: 5, 8, 12, 6, 8 и 10, мы видим, что число 8 встречается дважды, тогда как остальные числа встречаются по одному разу. Таким образом, мода для данного набора чисел равна 8.

В зависимости от вашей конкретной задачи и набора данных, вы можете использовать разные способы определения средних пропорций. Важно понять, какой метод наиболее подходит для вашей ситуации и использовать его соответствующим образом.

Надеюсь, эта информация помогла вам понять, как определить средние пропорции. Если у вас есть вопросы, не стесняйтесь задавать их!

Крайние и средние пропорции: определение и примеры использования

Простейший пример крайней пропорции можно найти в геометрии, в соотношениях длин сторон подобных треугольников. Если два треугольника подобны, то отношения длин соответствующих сторон будут крайними пропорциями. Например, в прямоугольном треугольнике длина гипотенузы будет к длине одного из катетов также, как длина этого катета к длине другого катета.

Средние пропорции также имеют широкое применение в науке и практике. Например, формула для вычисления скорости, известная как формула средней пропорции, говорит, что скорость равна произведению расстояния на время. Также, в статистике, средние пропорции используются для определения средней величины, среднеквадратического отклонения и других статистических показателей.

Примеры использования крайних и средних пропорций:

• В фотографии: соотношение золотого сечения используется для создания эстетически приятного композиционного решения.
• В архитектуре: использование пропорций Фибоначчи (крайней пропорции) позволяет создавать гармоничные и пропорциональные строения.
• В финансовой аналитике: использование средних пропорций позволяет анализировать и прогнозировать изменения цен на фондовом рынке.
• В спорте: определение оптимальных пропорций тела спортсмена позволяет улучшить его результаты.