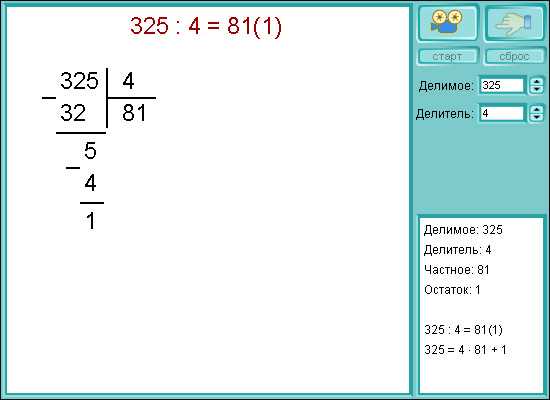
Когда мы говорим о числах, мы часто сталкиваемся с понятиями «кратные числа» и «делители». Но что же они означают и как с ними работать? Кратные числа — это числа, которые делятся на другое число без остатка. Например, числа 12 и 24 являются кратными числами числа 6, так как они делятся на 6 без остатка.
С другой стороны, делители — это числа, на которые данное число делится без остатка. Например, делителями числа 12 являются 1, 2, 3, 4, 6 и 12.
Работать с кратными числами и делителями очень полезно, когда мы решаем задачи или выполняем различные математические операции. В следующих разделах мы рассмотрим, как определить кратные числа, как найти делители и как использовать эти знания в практических примерах.
Кратные числа и делители
Давай начнем с определения. Кратные числа — это числа, которые можно получить путем умножения другого числа на целое число. Например, 4 и 8 являются кратными числами, так как 8 можно получить, умножив 4 на 2. Понятно?
А теперь рассмотрим делители. Делитель — это число, на которое заданное число делится без остатка. Например, делителями числа 12 являются 1, 2, 3, 4, 6 и само число 12. Все эти числа делятся на 12 без остатка.
Теперь давай посмотрим, как работать с кратными числами и делителями. Часто нас просят найти все кратные или делители числа. Для этого нужно просто делить число на возможные делители и проверять, делится ли оно без остатка. Если делится, то это делитель или кратное числа.
Давай рассмотрим пример. Представь, у нас есть число 20. И мы хотим найти все его кратные числа. Нам нужно поделить 20 на разные числа и проверять, делится ли оно без остатка. Делители числа 20 — 1, 2, 4, 5, 10 и само число 20. И все эти числа являются кратными числа. Понятно до сих пор?
А теперь задание для тебя! Попробуй найти все кратные числа числа 15. Уверен, ты справишься! Пиши мне результаты, я буду ждать!
В результате нашего разговора ты узнал, что кратные числа — это числа, которые можно получить умножением другого числа на целое число, а делители — это числа, на которые заданное число делится без остатка. И мы научились находить кратные числа и делители числа, просто деля его на разные числа и проверяя, делится ли оно без остатка.
Надеюсь, тебе было интересно узнать о кратных числах и делителях! Продолжай интересоваться математикой, и она откроет перед тобой много удивительных возможностей!
Определение кратных чисел
В математике мы часто сталкиваемся с понятием кратных чисел. Но что это такое и как мы можем работать с ними?
Кратные числа — это числа, которые делятся на другие числа без остатка. Другими словами, если одно число делится на другое, является его кратным. Например, число 10 является кратным числа 5, потому что оно делится на 5. Если мы разделим 10 на 5, мы получим 2 без остатка.
Кратность числа может быть определена с помощью деления с остатком. Если при делении одного числа на другое получается остаток 0, то оно будет кратным числу, на которое мы делили.
Например, рассмотрим число 15. Если мы разделим его на 3, мы получим остаток 0, что означает, что 15 является кратным числу 3. В этом случае 15 делится на 3 без остатка.
Кратные числа могут быть использованы для различных математических операций, таких как упрощение дробей или поиск общего кратного. Например, для упрощения дроби 6/12 мы можем найти общий кратный чисел 6 и 12, который будет являться их наименьшим общим кратным. В этом случае, общим кратным будет число 12, так как и 6, и 12 кратны ему.
Кратные числа также полезны при работе с последовательностями или таблицами чисел. Например, если мы строим таблицу умножения для числа 5, мы будем видеть, что все числа, которые делятся на 5 без остатка, будут являться его кратными.
Зная определение кратных чисел, мы можем использовать их в своих математических решениях и расчетах. Понимание этого понятия поможет нам лучше понять, как работает математика в нашей повседневной жизни.
Определение делителей
Понимание делителей является важным основополагающим принципом в математике, поскольку делители позволяют нам анализировать и работать с числами более подробно. Использование делителей может быть полезно в различных математических задачах, таких как факторизация чисел, нахождение наибольшего общего делителя и т. д.
Для определения делителей числа нужно проверить все числа от 1 до самого числа на делимость. Если число делится без остатка, то оно является делителем заданного числа. Например, для числа 24 мы проверяем делимость на числа 1, 2, 3, 4, 6, 8, 12 и 24. Если число делится без остатка на одно из этих чисел, то это число является делителем числа 24.
Определение делителей может помочь нам не только в абстрактных математических задачах, но и в повседневной жизни. Например, если у нас есть определенное количество предметов, то мы можем использовать делители, чтобы разделить их на равные группы или найти наибольшее количество групп, которое мы можем сформировать.
Итак, делители – это ключевой элемент в понимании и работе с числами. Знание делителей позволяет нам углубленно изучать числовые свойства и использовать их в решении различных задач. Не забывайте о делителях, они могут быть вашими лучшими помощниками в мире чисел!
Как найти делители числа?
Все мы знаем, что число может быть поделено на другое число без остатка. И эти числа, на которые оно делится, называются делителями. Но как именно найти эти делители?
Способов, как найти делители числа, существует несколько. Один из самых простых способов — это перебор всех чисел от 1 до самого числа и проверка, делится ли оно на каждое из них. Но это может оказаться долгим и утомительным процессом, особенно если число очень большое.
Более эффективным методом является нахождение делителей через простые числа. Для этого необходимо разложить число на простые множители и найти все возможные комбинации этих множителей.
Давайте рассмотрим пример. Пусть у нас есть число 12. Простыми множителями этого числа являются 2 и 3. Разложим число 12 на простые множители: 12 = 2 * 2 * 3. Теперь мы можем составить все возможные комбинации этих множителей: 1, 2, 3, 4, 6, 12.
Таким образом, делителями числа 12 являются 1, 2, 3, 4, 6 и 12.
Также стоит отметить, что ноль и само число также являются делителями любого числа. Например, делителями числа 5 являются 1, 5 и само число 5.
Найти делители числа можно также с помощью таблицы делителей. Для этого нужно записать все числа, на которые оно делится без остатка, в порядке возрастания. Например, для числа 10 таблица будет выглядеть следующим образом:
| 1 | 2 | 5 | 10 |
Простым методом для нахождения делителей числа является проверка всех чисел от 1 до квадратного корня из этого числа. Если число делится на какое-либо из этих чисел без остатка, то оно является делителем. Например, для числа 25 проверяем числа от 1 до 5 (квадратный корень из 25):
- 1: 25 делится без остатка
- 2: 25 не делится без остатка
- 3: 25 не делится без остатка
- 4: 25 не делится без остатка
- 5: 25 делится без остатка
Таким образом, делителями числа 25 являются 1 и 5.
Надеюсь, эти примеры помогут вам лучше понять, как найти делители числа. И помните, что делители — это ключевые элементы при работе с кратными числами и может быть полезно знать, как их находить.
Свойства кратных чисел и делителей

Во-первых, давайте разберемся, что такое кратные числа и делители. Кратное число — это число, которое делится на другое число без остатка. Например, 10 — кратное число для 5, потому что 10 делится на 5 без остатка. Делитель — это число, на которое другое число делится без остатка. Например, 5 — делитель для числа 10.
Теперь перейдем к свойствам кратных чисел и делителей:
- Свойство кратности: если число A кратно числу B, то оно также кратно всем кратным числам числа B. Например, если 10 кратно 5, то оно также кратно 15, 20, 25 и т.д.
- Свойство делимости: если число A делится на число B, то оно также делится на все делители числа B. Например, если 15 делится на 5, то оно также делится на 1, 3 и 15.
- Простое число: число, которое делится нацело только на 1 и на само себя. Простые числа имеют только два делителя. Например, 2, 3, 5, 7 — простые числа.
- Составное число: число, которое имеет более двух делителей. Например, 6, 8, 9 — составные числа.
- Наименьший общий делитель (НОД): это наименьшее число, которое делится нацело на два или более числа. Например, НОД для чисел 12 и 18 равен 6.
- Наибольший общий делитель (НОК): это наибольшее число, на которое делятся без остатка два или более числа. Например, НОК для чисел 4 и 6 равен 12.
Знание этих свойств помогает нам лучше понять числа и их взаимоотношения. Они используются при решении задач, разложении чисел на простые множители, нахождении НОД и НОК.
Итак, свойства кратных чисел и делителей — это мощный инструмент, который помогает нам лучше понять мир чисел и упростить работу с ними. Используя эти свойства, мы можем выполнять математические операции с большей уверенностью и эффективностью.
Кратные числа и делители: что это такое и как работать с ними
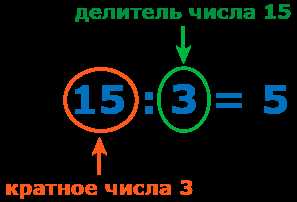
Например, число 10 делится без остатка на 2, так как 10 = 2 * 5. В этом случае число 2 является делителем числа 10, а число 10 является кратным числом для числа 2.
Для работы с кратными числами и делителями часто используются таблицы умножения и деления. Таблица умножения позволяет найти все кратные числа для данного числа, а таблица деления помогает найти все делители для данного числа.
Например, для числа 4 таблица умножения даст нам следующие кратные числа: 4, 8, 12, 16, 20 и так далее. А таблица деления для числа 30 покажет нам следующие делители: 1, 2, 3, 5, 6, 10, 15, 30.
Еще один способ работы с кратными числами и делителями — это нахождение наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) для двух или более чисел. НОД — это наибольший из всех их общих делителей, а НОК — это наименьшее число, которое делится на все заданные числа без остатка.
Например, для чисел 12 и 18 НОД равен 6, так как эти числа имеют общие делители 1, 2, 3 и 6, и 6 является наибольшим из них. НОК для этих двух чисел равен 36, так как это наименьшее число, которое делится на 12 и 18 без остатка.
Использование кратных чисел и делителей в математике позволяет решать различные задачи, в том числе находить общие кратные и делители, находить НОД и НОК, а также проводить умножение и деление чисел.