Кратные и дольные единицы в математике: понятие и особенности

Математика является одной из самых важных и фундаментальных наук, и одним из ее ключевых понятий являются кратные и дольные единицы. Эти понятия играют важную роль в различных областях математики, включая арифметику, алгебру и геометрию.

Кратные и дольные единицы представляют собой особые числа, которые связаны с определенной базовой единицей. Кратная единица означает, что число делится на данную базовую единицу без остатка, в то время как дольная единица означает, что число является частью данной базовой единицы.

Понимание и использование кратных и дольных единиц помогает математикам решать сложные задачи и разрабатывать новые алгоритмы и методы. Эти понятия также находят свое применение в реальном мире, например, в физике, экономике и других науках.

Понятие кратных и дольных единиц

Когда мы говорим о числах и их отношении друг к другу, неизбежно сталкиваемся с понятиями кратных и дольных единиц. Это важные математические концепции, которые помогают нам понять и описать различные отношения между числами.

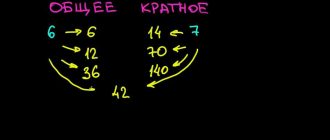
Начнем с понятия кратных единиц. Кратность — это свойство чисел, которое указывает на то, насколько одно число «вмещается» в другое число. Например, 6 является кратным числом числа 3, потому что 3 «вмещается» в 6 два раза без остатка. В общем случае, если одно число делится на другое без остатка, то первое число будет кратным второго числа.

Давайте рассмотрим конкретный пример, чтобы лучше понять это понятие. Представим, что у нас есть школьный класс, в котором 24 ученика. Мы хотим узнать, сколько учеников в нем составляют одну группу. Если мы разделим общее количество учеников (24) на размер группы (например, 6), мы получим 4. Это значит, что 24 ученика составляют 4 группы по 6 учеников в каждой. Таким образом, мы можем сказать, что число 6 — кратное число для числа 24.

Теперь перейдем к понятию дольных единиц. Если кратные единицы указывали на количество раз, которое одно число содержится в другом, то дольные единицы указывают на то, какую часть от одного числа составляет другое число.

Опять же, разберемся с этим на примере. Представим, что у нас есть 8 яблок и мы хотим поделить их поровну между 2 друзьями. В этом случае каждый друг получит по 4 яблока, что составляет половину общего количества яблок. Мы можем сказать, что число 4 — дольное число для числа 8, так как оно составляет половину от него.

Взаимодействие между кратными и дольными единицами может помочь нам лучше разобраться в отношениях между числами. Их использование дает нам инструменты для анализа и описания различных свойств и закономерностей числовых систем.

Понимание понятий кратных и дольных единиц в математике помогает нам развивать навыки логического мышления, аналитического мышления и решения проблем. Они также широко используются в других областях науки и повседневной жизни, таких как физика, экономика и торговля.

Кратные единицы

В математике кратные единицы имеют большое значение, так как они позволяют нам представить и сравнивать большие числа, а также проводить различные операции с ними. Например, в системе десятичных чисел мы используем кратные единицы, такие как десятки, сотни и тысячи, чтобы представить числа, превышающие десятичные пределы.

Примеры кратных единиц в различных системах чисел:

• В двоичной системе мы используем кратные единицы — двойки, четверки, восьмерки, чтобы представить числа больше единицы.
• В восьмеричной системе кратные единицы — это восемь, шестнадцать, тридцать два и так далее.
• В шестнадцатеричной системе используются кратные единицы — шестнадцать, тридцать два, шестьдесят четыре и так далее.

Использование кратных единиц в математике не ограничивается только представлением чисел. Они также помогают в проведении различных операций, таких как сложение, вычитание, умножение и деление.

Зная понятие кратных единиц, мы можем легко представить и сравнивать числа разной величины. Например, если нам нужно сравнить 100 и 1000, мы знаем, что 1000 больше, так как это 10 крат единицы 100.

Кратные единицы представляют собой мощный инструмент в математике, который позволяет нам работать с числами различных величин и проводить различные операции с ними. Они помогают нам анализировать и понимать мир вокруг нас, открывая перед нами возможности для исследования и открытия новых знаний.

Дольные единицы

Дольные единицы часто используются в ежедневной жизни. Например, когда мы говорим о половине пиццы, третьей части пирога или четверти галона молока. Долями можно выражать и время, например, полчаса или третью часть дня.

Одной из самых распространенных дольных единиц является десятичная система счисления, в которой используются числа после запятой. Например, 1,5 представляет собой одну целую и половину, а 0,25 — четверть целого числа.

Также дольные единицы используются в математике для изучения дробей. Дроби представляют часть целого числа и записываются в виде дроби, где числитель указывает количество долей, а знаменатель указывает общее количество равных долей. Например, дробь 3/4 означает три четверти целого числа.

Примеры дольных единиц:

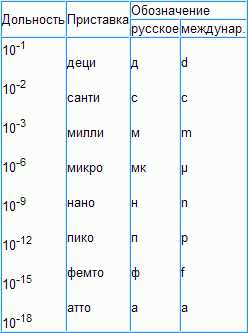
• Половина (1/2)
• Треть (1/3)
• Четверть (1/4)
• Пятая часть (1/5)
• Десятая часть (1/10)

Дольные единицы используются не только для измерения и представления долей, но и для сравнения различных количеств. Например, мы можем сказать, что 2/3 больше, чем 1/3, или что половина яблоки меньше, чем целое яблоко.

Знание о дольных единицах имеет практическое и теоретическое значение. Оно помогает нам разбираться в повседневных ситуациях, таких как покупка продуктов, измерение времени или сравнение размеров объектов. В математике дольные единицы являются основой для изучения дробей и десятичных чисел, что помогает нам развивать абстрактное мышление, решать сложные задачи и применять этот навык в различных областях нашей жизни.

Кратные и дольные единицы в числовых системах

Во-первых, давайте вспомним, что такое кратное число. Кратными называются числа, которые получаются умножением какого-либо числа на другое целое число. Например, 12 является кратным числом для числа 3, потому что 12 = 3 * 4.

А теперь представьте себе, что мы находимся в другой числовой системе. Например, в десятичной системе, которую мы используем в повседневной жизни, основание равно 10. Это означает, что мы используем 10 различных цифр (0-9) для обозначения чисел.

Теперь представьте себя в числовой системе с другим основанием, скажем, 8 или 16. В этих системах нам нужно использовать соответствующее количество цифр (0-7 для основания 8 и 0-9, а также A-F для основания 16), чтобы обозначить числа.

И вот тут начинаются интересные вещи. В числовых системах с основанием, отличающимся от 10, кратные числа выглядят несколько иначе. Например, восьмеричная система имеет свои собственные кратные числа, которые получаются умножением числа на другое целое число:

• Восьмеричное число 10 (десятичное число является кратным числом для числа 2.
• Восьмеричное число 20 (десятичное число 16) является кратным числом для числа 4.
• И так далее.

То же самое относится и к шестнадцатеричной системе. Здесь также есть свои кратные числа, получаемые умножением числа на другое целое число:

• Шестнадцатеричное число 10 (десятичное число 16) является кратным числом для числа 2.
• Шестнадцатеричное число 20 (десятичное число 32) является кратным числом для числа 4.
• И так далее.

Интересно, правда? В числовых системах с основаниями, отличными от 10, кратные числа имеют свою собственную уникальную структуру.

Теперь перейдем к дольным числам. Дольные числа — это числа, которые являются долей какого-либо числа в конкретной числовой системе. Например, в десятичной системе мы имеем дольные числа в виде десятых (0.1), сотых (0.01) и так далее.

А в числовых системах с другими основаниями мы также можем иметь свои собственные дольные числа. Например, восьмеричная система имеет дольные числа в виде восьмеричных долей (0.1), шестнадцатеричная система имеет дольные числа в виде шестнадцатеричных долей (0.1).

Мы видим, что в каждой числовой системе кратные и дольные числа имеют свои особенности и структуру. Изучение этих особенностей может помочь нам лучше понять и использовать различные системы счисления в нашей повседневной жизни, а также в научных и технических областях.

Итак, теперь, когда вы понимаете, что такое кратные и дольные числа в числовых системах, задайте себе вопрос: какая из них вызывает больше волнения возможностей и разнообразия?

Кратные и дольные единицы в десятичной системе

В десятичной системе счисления каждый разряд числа представляет собой определенную степень числа 10. Например, число 352 можно представить как 3 * 10^2 + 5 * 10^1 + 2 * 10^0. В этом представлении каждый разряд умножается на соответствующую степень числа 10, поэтому они являются кратными единицам, а именно 100, 10 и 1.

Кроме того, в десятичной системе счисления возможно представление дробных чисел. Дробное число состоит из целой части и дробной части, разделенных десятичной запятой. Например, число 3,14 может быть представлено как 3 + 0,1 * 1 + 0,01 * 4. Здесь целая часть (3) является дольной единицей, а дробная часть (0,1 и 0,01) является кратными дольными единицами.

Кратные и дольные единицы имеют важное значение при выполнении математических операций в десятичной системе счисления, таких как сложение, вычитание, умножение и деление. При сложении чисел важно выравнивать их по разрядам, чтобы правильно складывать кратные и дольные единицы. При выполнении умножения и деления также требуется учет кратных и дольных единиц, чтобы правильно определить разряды результата.

Понимание кратных и дольных единиц в десятичной системе счисления помогает нам лучше понять структуру чисел и выполнять математические операции более точно. Оно также имеет важное практическое применение в повседневной жизни, например, при работе с деньгами, измерением времени и расчетами в науке и технике.

Таким образом, знание кратных и дольных единиц в десятичной системе счисления является неотъемлемой частью математической грамотности и помогает нам лучше понимать и использовать мир чисел вокруг нас. Необходимы такие знания как базовый фундамент, чтобы развиваться не только в математике, но и в других областях, требующих решения математических проблем и задач. Давайте продолжим изучение и применение этих определений для нашего личного и профессионального роста!

Кратные и дольные единицы в двоичной системе

В двоичной системе также применяются понятия кратных и дольных единиц, аналогичные десятичной системе. Кратными единицами в двоичной системе считаются числа, которые могут быть разделены на другое число без остатка. Например, число 10 является кратным единицей для числа 5, потому что оно делится на 5 без остатка.

Дольными единицами в двоичной системе считаются числа, которые являются долей другого числа. Например, число 01 является дольной единицей для числа 10, потому что оно представляет половину числа 10.

Кратные и дольные единицы играют важную роль в двоичной системе, так как с их помощью можно представлять и выполнять различные операции с числами. Например, для представления чисел с большим количеством разрядов используются кратные единицы, а для уменьшения количества разрядов — дольные единицы.

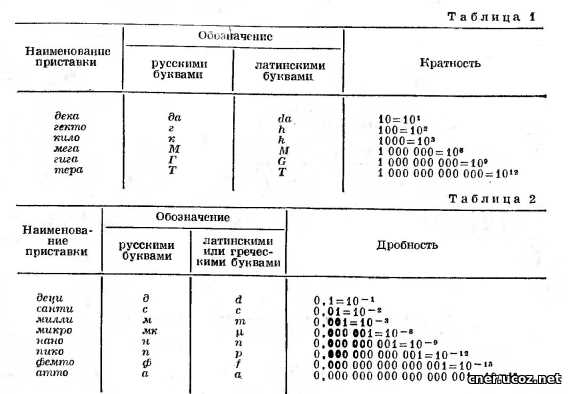
Также в двоичной системе можно использовать префиксы для обозначения кратных и дольных единиц. Например, префикс «k» (кило) обозначает 1024 (2^10), а префикс «m» (мега) обозначает 1048576 (2^20).

Итак, использование кратных и дольных единиц в двоичной системе позволяет удобно представлять и выполнять операции с числами. Это важное понятие для понимания работы компьютеров и других электронных устройств.

Применение кратных и дольных единиц

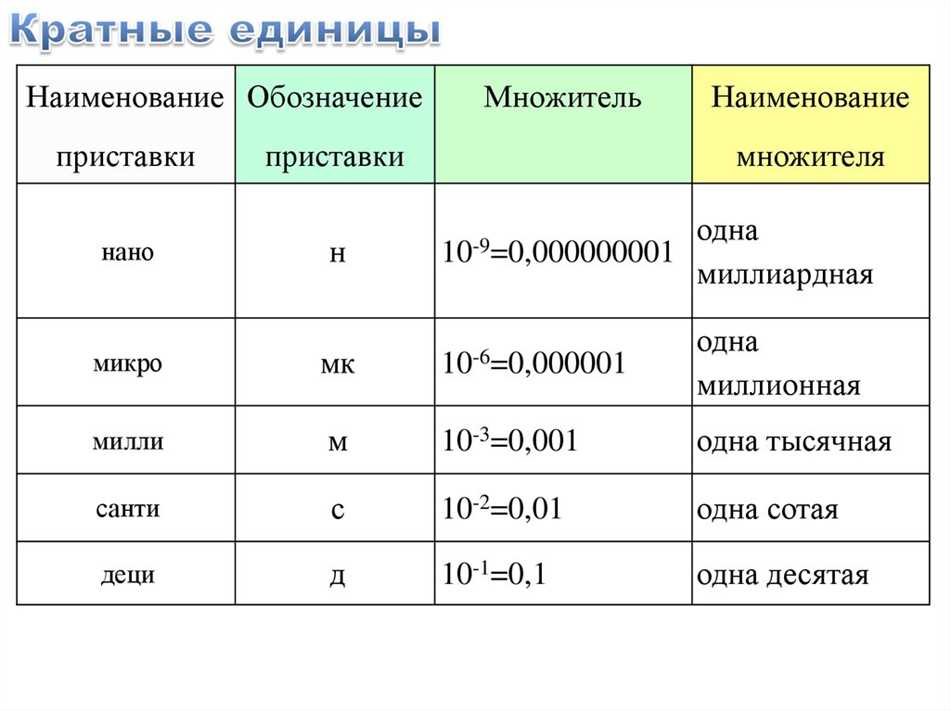
Использование кратных и дольных единиц особенно полезно при работе с величинами и измерениями. Например, килограмм — это кратная единица массы, которая используется для измерения веса любых предметов. Грамм является дольной единицей, которая помогает нам измерять массу более мелких предметов. Таким образом, мы можем оценивать и сравнивать массу разных предметов, а также проводить операции сложения и вычитания с этими единицами.

Кроме того, кратные и дольные единицы применяются в длине, объеме, времени и других измерениях. Например, метр — это кратная единица длины, которая используется для измерения расстояний, высоты и других размеров. Сантиметр и миллиметр являются дольными единицами, которые позволяют нам измерять более мелкие объекты и задавать более точные размеры.

Применение кратных и дольных единиц также находит свое применение в деньгах и валютах. Например, доллары и рубли — это кратные единицы валюты, которые помогают нам оценивать и сравнивать стоимость товаров и услуг. Копейки и центы являются дольными единицами, которые используются для работы с более мелкими денежными суммами.

Кроме того, кратные и дольные единицы играют важную роль в науке, инженерии и технологиях. Например, киловатт — это кратная единица мощности, которая используется для измерения энергии, а мегабайт — это кратная единица для измерения объема информации. Биты и байты являются дольными единицами, которые используются для измерения количества информации в компьютерных системах.

Таким образом, применение кратных и дольных единиц является неотъемлемой частью нашей повседневной жизни и позволяет нам проводить измерения, оценивать стоимость, сравнивать различные величины и выполнять различные математические операции. Понимание и использование этих единиц позволяют нам лучше понять и описать мир вокруг нас.

Применение кратных единиц

Кратные единицы используются в различных областях нашей жизни и в математике они играют важную роль. Они позволяют нам измерять и сравнивать различные физические величины, такие как масса, длина, время и т.д. Кратные единицы упрощают нашу жизнь и помогают нам понять мир вокруг нас.

Например, килограмм — это кратная единица измерения массы. Она используется везде, от супермаркета до медицинских учреждений. Когда мы покупаем продукты в супермаркете, мы указываем массу продукта в килограммах. Когда мы занимаемся спортом, наша масса также измеряется в килограммах. Эта единица измерения универсальна и понятна всем.

Еще одним примером кратной единицы может быть метр. Метр — это единица измерения длины. Мы используем ее, чтобы измерить расстояние между двумя точками или длину объекта. Например, когда мы строим дом или покупаем новую мебель, мы используем метры, чтобы понять, какого размера они будут. Метры также используются в спортивных соревнованиях, чтобы измерить дистанцию.

Кратные единицы также играют важную роль в математике. Например, мы используем кратные единицы для выполнения арифметических операций, таких как сложение, вычитание, умножение и деление. Когда мы складываем два числа, мы выражаем результат с помощью той же кратной единицы, которая использовалась для измерения исходных чисел. Например, если мы складываем 2 метра и 3 метра, мы получим 5 метров.

Кратные единицы играют ключевую роль в нашей жизни и в математике. Они помогают нам понять мир вокруг нас и избегать путаницы при измерении и сравнении различных физических величин. Использование кратных единиц делает нашу жизнь проще и более удобной. Так что следующий раз, когда вы увидите кратную единицу, задайте себе вопрос: «Как я могу использовать ее, чтобы сделать свою жизнь лучше?»

Кратные и дольные единицы в математике: понятие и особенности

Примером кратных единиц может служить метр. Если длина отрезка равна 2 метрам, то он является кратным единице, так как его можно разделить на два отрезка длиной по 1 метру каждый.

Примером дольной единицы может служить градус. Градус можно разделить на минуты и секунды. 1 градус равен 60 минутам, а каждая минута равна 60 секундам.

Для удобства использования в математике, кратные и дольные единицы часто используются в международной системе единиц. Например, в международной системе единиц для измерения массы используется килограмм, который является кратной единицей, так как его можно разделить на граммы.

Важно понимать, что кратные и дольные единицы в математике являются взаимосвязанными и служат для более удобного измерения и работы с числами. Они широко используются в различных областях науки и техники.